极大似然估计
极大似然估计, Maximum Likelihood Estimation, MLE.
wikipedia
思想
它是这样一种思想:
假设拿到的样本服从某种分布律, 估计分布律中的参数, 使得观测样本序列发生的概率最大.
换种说法就是, 事情已经发生了, 求一个模型中的参数, 使得已发生的现象解释起来最为自然, 合理.
1.公式
P ( θ ∣ D ) = P ( D ∣ θ ) ∗ P ( θ ) P ( d a t a ) P(θ|D) = \frac{P(D|θ) * P(θ)} {P(data)} P(θ∣D)=P(data)P(D∣θ)∗P(θ)
最大似然估计中的采样需满足一个很重要的假设, 就是所有的采样都是独立同分布的。
< { x 1 , x 2 , . . . , x n } , θ , P ( ⋅ ) > <\{x_1,x_2,...,x_n\}, \theta, P(\cdot)> <{x1,x2,...,xn},θ,P(⋅)>依次为独立同分布的采样, 模型中的参数, 模型的概率函数.
则
(1.1) P ( x 1 , x 2 , . . . , x n ∣ θ ) = ∏ i = 1 n P ( x i ∣ θ ) P(x_1,x_2,...,x_n|\theta)=\prod_{i=1}^nP(x_i|\theta) \tag {1.1} P(x1,x2,...,xn∣θ)=i=1∏nP(xi∣θ)(1.1)
令似然函数等于式(1.1)得到:
(1.2) L ( θ ; x 1 , x 2 , . . . , x n ) = P ( x 1 , x 2 , . . . , x n ∣ θ ) = ∏ i = 1 n P ( x i ∣ θ ) L(\theta; x_1,x_2,...,x_n )=P(x_1,x_2,...,x_n|\theta)=\prod_{i=1}^nP(x_i|\theta) \tag {1.2} L(θ;x1,x2,...,xn)=P(x1,x2,...,xn∣θ)=i=1∏nP(xi∣θ)(1.2)
为了方便计算, 对等号两边取对数得到:
(1.3) ln L ( θ ; x 1 , x 2 , . . . , x n ) = ∑ i = 1 n ln P ( x i ∣ θ ) \ln L(\theta; x_1,x_2,...,x_n)= \sum_{i=1}^n \ln P(x_i|\theta) \tag {1.3} lnL(θ;x1,x2,...,xn)=i=1∑nlnP(xi∣θ)(1.3)
其中 ln L ( ⋅ ) \ln L(\cdot) lnL(⋅)称为对数似然, 令其最大得到待求的 参数.
(1.4) θ ^ = arg max θ ln L ( θ ; x 1 , x 2 , . . . , x n ) \hat \theta=\arg\max_\theta \ \ln L(\theta; x_1,x_2,...,x_n) \tag{1.4} θ^=argθmax lnL(θ;x1,x2,...,xn)(1.4)
2.例子
一个罐子里面有黑白两种颜色的球, 我们有放回地随机拿出一个球, 做了三次实验, 结果是 <白, 白, 黑>. 根据这个实验来估计罐中白球的比例。
很直观的答案就是2/3, 而其后的理论支撑是什么呢? 就是 极大似然估计.
- 模型
二项分布 - 参数
得到白球的概率为p, 得到黑球的概率为(1-p). - 样本
A=<白, 白, 黑>, 得到这一现象的概率为
(2.1) P ( A ) = p 2 ( 1 − p ) = − p 3 + p 2 P(A)=p^2(1-p)=-p^3+p^2 \tag {2.1} P(A)=p2(1−p)=−p3+p2(2.1)
下面开始计算.
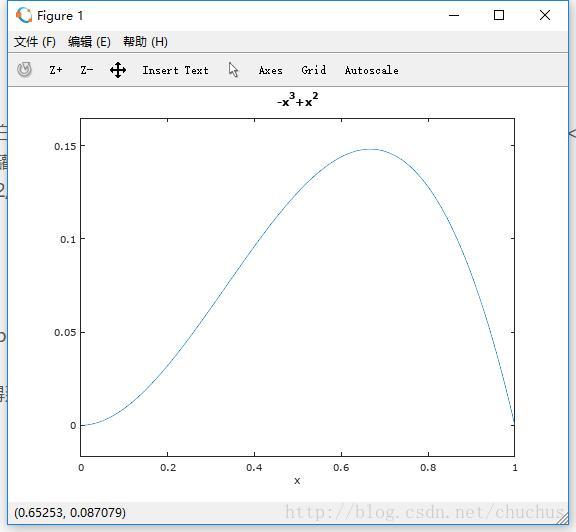
图2-1 y = − x 3 + x 2 , x ∈ [ 0 , 1 ] y=-x^3+x^2 , x \in [0,1] y=−x3+x2,x∈[0,1] 的图像
从该图可以方便地看出极大值点在 x = 2 3 ≈ 0.67 x=\frac23 \approx 0.67 x=32≈0.67处取得.
我们也可以对 式(2.1) 进行求导并令其等于0, 得到方程 − 3 p 2 + 2 p = 0 -3p^2+2p=0 −3p2+2p=0, 解得p=2/3.