中级篇——最小生成树
最小生成树可以解决一类最短路径问题，现在给出一幅图：
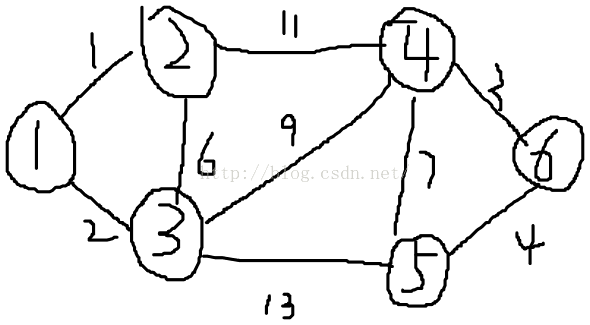每条路上的数值代表权值。现在需要从1到6找一条最便捷的路径。
第一步：从1出发有1——2,1——3，两条边。1——2比1——3短，故先连通1——2。
第二步，接下来看1——3,2——3,2——4，三条边，1——3和2——3都能连通1,2,3三个点，但1——3明显小于2——3故连通2——3.
接下来，最短的边是4——6边权值为3，那就连上吧。再然后就是5——6边权值小，也连上！
从现在开始该思考了！剩下的边2——3最小，然而2,3已经连通，再连起来就不符合树的定义，同理4——5也是一样。只能在2——4,3——4,3——5中选择，此时3——4边权值最小，链接3——4。
最小生成树诞生！
回顾刚才的步骤，首先判断两个点是否连通，优先选择边权值小的点加入树中，重复步骤即可。最先就是将所给的边按照全值从小到大排列，那么怎么判断两个点是否连通？这就需要之前讲过的并查集算法，套模板即可。这种最小生成树的方法叫做最小生成树的Kruskal算法。
以本题为例，代码实现如下：
#include
using namespace std;
struct edge
{
int u,v,w;//记录起点终点边长
}a[1005];
int n,m;
int f[1005],sum,cnt;//并查集要用到的东西
void quicksort(int left,int right)
{
int i=left,j=right;
struct edge t;
if(left>right) return ;
while(i!=j)
{
//顺序很重要，先从右边开始
while(a[j].w>=a[left].w&&i>n>>m)
{
cnt=0;sum=0;
for(int i=1;i<=m;i++)
{
cin>>a[i].u>>a[i].v>>a[i].w;
}
quicksort(1,m);//按权值排序
//并查集初始化
for(int i=1;i<=n;i++)
f[i]=i;
//Kruskal算法核心
for(int i=1;i<=m;i++)
{
if(join(a[i].u,a[i].v))//判断是否已经连通
{
cnt++;sum+=a[i].w;
}
if(cnt==n-1) break;//n个点链接只需n-1条边
}
cout< 上面介绍的是kruskal最小生成树法，主要步骤就是将边按照边权值大小排序并查看点与点是否在一条路径上。而下面这种算法是prim最小生成树法，其与最短路径时的Dijkstra算法相似（真TM极其相似），而且代码长度短于kruskal算法。
算法步骤：
一：从一点构造最小生成树，假设从1点开始。将1加入树中，用一个一维数组vis[]来标记每个点是否在树中。
二：用dis[]数组记录生成树到各顶点的距离。初始化时，与1有直接连边的赋值为其边权值，无连边的设为无穷大。
三：从树中选出离起点最近的点加入到生成树中，按照Dijkstra算法松弛各边。
四：重复第三步，直至树中有n个点为止。
代码实现：
#include
#define max 9999999
using namespace std;
int n,m,dis[1005],vis[1005],e[1005][1005];
int u,v,w,cnt,sum;
int main()
{
while(cin>>n>>m)
{
cnt=0;sum=0;
for(int i=1;i<=n;i++)
{
vis[i]=0;
for(int j=1;j<=n;j++)
{
if(i==j) e[i][j]=0;
else e[i][j]=max;
}
}
while(m--)
{
cin>>u>>v>>w;
e[u][v]=e[v][u]=w;
}
for(int i=1;i<=n;i++)
dis[i]=e[1][i];
//核心代码，将起点加入树中，记得cnt++
vis[1]=1;cnt++;
while(cnte[u][v])
dis[v]=e[u][v];
}
}
cout< 这种方法的运算时间是O(N^2)，已经还可以了，但如果利用堆进行优化时间可降为O(MlogN)。对的优化之后会讲！
hdu1102
We know that there are already some roads between some villages and your job is the build some roads such that all the villages are connect and the length of all the roads built is minimum.
Then there is an integer Q (0 <= Q <= N * (N + 1) / 2). Then come Q lines, each line contains two integers a and b (1 <= a < b <= N), which means the road between village a and village b has been built.
#include
#define max 9999999
using namespace std;
int n,m,dis[1005],vis[1005],e[1005][1005];
int u,v,w,cnt,sum;
int main()
{
while(cin>>n)
{
cnt=0;sum=0;
for(int i=1;i<=n;i++)
{
vis[i]=0;
for(int j=1;j<=n;j++)
{
if(i==j) e[i][j]=0;
else e[i][j]=max;
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
cin>>w;
if(w>m;
while(m--)
{
cin>>u>>v;
e[u][v]=e[v][u]=0;
}
for(int i=1;i<=n;i++)
dis[i]=e[1][i];
//核心代码，将起点加入树中，记得cnt++
vis[1]=1;cnt++;
while(cnte[u][v])
dis[v]=e[u][v];
}
}
cout<