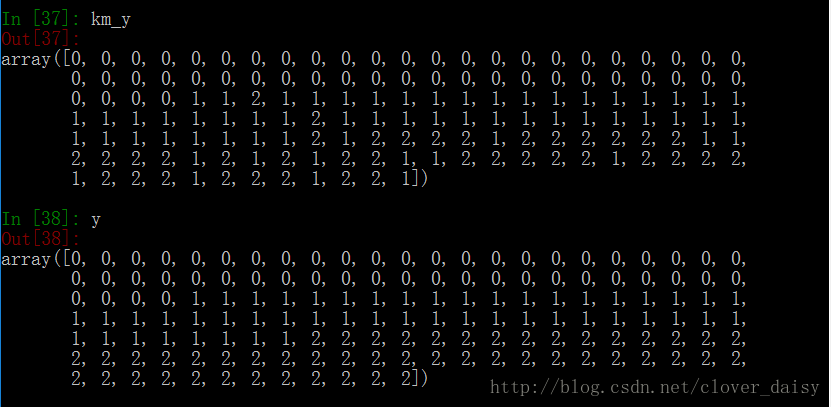sklearn基本用法----knn
K-nn算法
1.定义
在模式识别中,k-邻近算法(k-nn)是用于分类和回归的非参数方法。所谓K邻近,就是k个最近的邻居,意思是每个样本都可以用它最接近的k个邻居来代表。
2.k-nn核心思想
knn算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。(给定一个待分类数据,通过距离计算得到离它最近的k个样本,由k个样本投票决定待分类数据归为哪一类—”少数服从多数“)
3.算法流程
计算样本数据和待分类数据的距离。
选择k个与待分类数据距离最近的样本。
统计出k个样本中大多数样本所属的分类,将该类记作category。
待分类数据属于category。
4.算法优缺点
(1)优点
简单,易理解,易实现。
适合对稀有事件进行分类。
- 适合多分类问题(multi-modal,对象有多个类别标签),k-nn比svm更合适。
(2)缺点
当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。
计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
鸢尾花数据集为例讲述k-nn算法
from sklean import datasets,neighbors
iris = datasets.load_iris()
X = iris.data
y = iris.target
kn_clf = neighbors.KNeighborsClassifier()
kn_clf.fit(X,y)
kn_y = kn_clf.predict(X)
print(kn_y)
print(y)
accuracy_knn = (kn_y == y).astype(int).mean()
print(accuracy_knn)
鸢尾花数据集示例svm算法
from sklearn import svm
clf = svm.SVC()
clf.fit(X,y)
s_y = clf.predict(X)
print(s_y)
print(y)
accuracy_svm = (s_y == y).astype(int).mean()
print(accuracy_svm) 鸢尾花数据集示例k-means算法
from sklearn import cluster
km = cluster.KMeans(n_clusters = 3)
km.fit(X)
km_y = km.predict(X)
print(km_y)
print(y)
accuracy_km = (km_y == y).astype(int).mean()
print(accuracy_km)