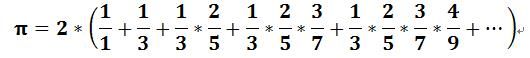圆周率与信息论
1.圆周率包含了宇宙奥秘?
圆周率是一个无理数,无理数 = 无限+不循环
很多人还认为它是个正规数,正规数 = 小数点后每个数字出现概率相等
所以,理论上说它可能包含了世界上的所有信息?
这个说法我最早在《信息简史》中看到,很多文章也有这样的说法:
你的生日,银行卡密码,大英百科,莎士比亚全集。。。还有,这篇文章,都可以找到
我们来这里https://www.1415926pi.com/看一下,它可以检测你所输入的序列出现在 的哪儿
比如我的银行卡密码:
在小数点后第10140332位成功查找到数字:4100591177 23345669889533959
哦,天呐,这么神奇吗?
难道是上帝设计宇宙的蓝图?
2.圆周率究竟包含了多少信息?
= 宇宙蓝图
宇宙蓝图 = 无穷无尽的信息量
= 无穷无尽的信息量
非常完美,证毕
等等,圆周率是怎么被计算出来的?
在一代代数学家的努力下,方法很多,我随便贴一个吧,无穷级数法
写代码计算一下,是不是非常简单:
public double PI(double z){ //z是精度
double sum=2;
int n=1;
int m=3;
double t=2;
while(t>z){
t=t*n/m;
sum=sum+t;
n++;
m+=2;
}
当然这里会受限于运行速度和语言本身的基本类型的限制,但是从逻辑角度而言没影响
也就是说,我给你一个不到1k的文档,你把它放进足够快的电脑跑一跑 = 我给了你宇宙蓝图
这么说来,难道。。。
我是上帝?
这里有的人会开始困惑,一方面, 中确确实实的包含了那些信息,我们也查到了
另一方面,显然我不是上帝,我除了那个程序外没有给你任何其他信息。结果你却可以得到那么多信息!
3.信息论基本概念复习小课堂
是信息,程序也是信息,莎翁全集也是信息。。。
这么混乱吗?信息到底是什么?
来分解一下,消息,信息容量,信息量,信息熵
我们真正要的那个,其实是信息量,就是:能让不确定性的减少,确定性增加的东西
也就是说,当一个事件发生概率无限大的时候,你告诉我了,也不会法消除什么不确定性,比如“男足不会夺冠”,也就是俗称的----“废话”,废话的信息量趋近于0.
那么具体信息量该怎么计算呢?
设该事件发生的概率为p,比如我面对一道我不会的单选,我选对正确答案B的概率p,是1/4
我的好朋友,学霸,好心人----小明给了我一个纸条,上面写了:“答案是B”
对我而言,小明的纸条中携带的信息是:log2(1/p)= log2(4)= 2bit
下一题,我听课了!了解!我知道一定不是C和D!我选对正确答案B的概率p,是1/2
我的好朋友,学霸,好心人----小明给了我一个纸条,上面写了:“答案是B”
对我而言,小明的纸条中携带的信息是:log2(1/p)= log2(2)= 1bit
小明给我的纸条就叫消息,消息是信息的载体,消息是具体的而信息是抽象的
我们在定义一个小球的热能时,知道要去了解它的质量,材质,温度,把条件限定起来
在定义纸条携带的信息时,把纸条限定住就够了么?当然不是
前面提到,即使小明的纸条没变,携带的信息量也是不一样的
“不确定性的增减”,是要和讨论的环境息息相关的,跟我是不是学霸是不是听课了是选择题还是判断题,相关的
那么之前说的“信息”,实则类似于这种说法:“一张纸条,很小,长度允许写2位,可以写0和1,所以它携带的信息量是2bit”
这个概念其实指的是纸条的信息容量,我们把它们给混淆了
4.我是上帝么?
有了上面的概念,这个问题可以被改写为:,或者说那个程序中,是否真的蕴含了无穷的信息?
又可以被改写为:是否减少了不确定性?
接受了教训,我们学会了要完整定义问题,上面那种描述是不严谨的:不确定?什么不确定?
我定义了如下几个问题:
1.给定或程序,请钢蛋从中找出一本《莎士比亚全集》,这样可以提供给我100000000000bit(乱写的)的信息量
结果:钢蛋根本不知道《莎士比亚全集》是啥,作为一个文盲,他甚至连《金瓶梅》都没看过,所以那个,连1bit都提供不了
2.钢蛋有或程序,也有《莎士比亚全集》,告诉我这本书出现在哪?
结果:相当于这样一个情况,我在考试,一道题的答案是ABCD(序列),在我完全不知道做的情况下,要知道正确答案的位置(《全集》的位置),看起来我现在需要log2(4/1) = 2bit的信息。
但是要想一下,这2bit的信息(比如“答案是B”),是这道题给我的么?是出题老师给我的么?难道不是我的好朋友,学霸,好心人----小明,给的吗?
也就是说,即使钢蛋告诉了我一个值,比如莎翁全集出现在1101010100110101010位,这个信息是钢蛋给我的,其实跟这个序列完全无关,序列仍然连1bit都没提供
3.紧接2,有人会问:如果你要的就是《莎翁全集》这本书的信息呢?这样虽然坐标位置是钢蛋提供的,但是《全集》的信息难道不是给你的么?怎么能说一无是处呢?一些有想象力的朋友可能会发现一个生财之道:
卖电子书
我找到你的淘宝店,在上面下单,买一本《莎士比亚全集》
你给我发了一段生产的代码+《全集》首次出现的位置+《全集》的长度
perfect!新的编码方式发现了!超大数据快速传输新方法发现了!图灵奖唾手可得!
好,生产的代码我们有了,现在缺首次出现位置了!未来的计算机很快,用暴力对比或者KMP匹配都可以秒找
那么,匹配序列的首位可能出现哪里呢?
设《全集》共有x位
随便在序列中选一个位置做开头,它匹配《全集》首位的概率是1/2(二进制编码),第二位也匹配的概率是1/2,照此循环,正确找到开头的概率p是:1/2^x,那么这个位置在序列中出现的期望长度 == 一个每次中奖概率为p的彩票,中奖一次的期望是买多少次?
ES = np = 1,n就是次数,n = 1/p,也就是2^x,首次出现的期望位置是2^x处
这是个位置,表示这个位置要多大的信息容量呢?log2(2^x)= x位
回头看一下:“设《全集》共有x位”
(╯-_-)╯╧╧
这像什么?像不像一次一密的加密过程?
顺便提一下量子加密通讯,一对纠缠粒子本身虽然能传递一些“消息”,但是由于表达的方式(比如偏振角)是随机的,其实完全没有传递任何信息,它传递的是密钥而非密文,密文还是要用经典信道传递的。这就好比我们的序列,它能传递一些东西,但并不是信息。举个例子,我们把一对手套拆散后包起来,你一只我一只,你走到天涯海角后打开一看,左手的,你马上就能知道我这里是右手的这一信息,但是能传递信息么?并不能,你能做的可能是在被窃听的线路上打电话给我:
“喂,帮我照顾一下我的生命之光,我的一生挚爱”
“哪个?”
“你那儿是左就是黄小姐,你那是右就是陈小姐,懂了吧,我不能多言”
“懂了,放心吧”。
这就是为什么真实有效的信息通讯还是要依赖传统信道,不能靠“玄学”。当然,也不能靠