（六）如何利用Python从头开始实现随机森林算法

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

---

（一）机器学习中的集成学习入门

（二）bagging 方法

（三）使用Python进行交易的随机森林算法

（四）Python中随机森林的实现与解释

（五）如何用 Python 从头开始实现 Bagging 算法

（六）如何利用Python从头开始实现随机森林算法

---

介绍

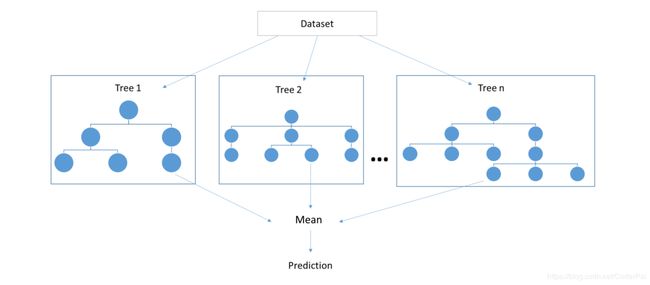
随机森林是集成学习中一个主要的算法。简而言之，集成方法是一种将几个弱学习器的预测结果进行组合，最终形成一个强学习器的方法。可以直观的猜测一下，随机森林通过减少过拟合来达到比决策树更好的效果。决策树和随机森林都可用于回归和分类问题。在这篇文章中，我们利用随机森林来解决一些问题。

理论

在开始编写代码之前，我们需要了解一些基本理论：

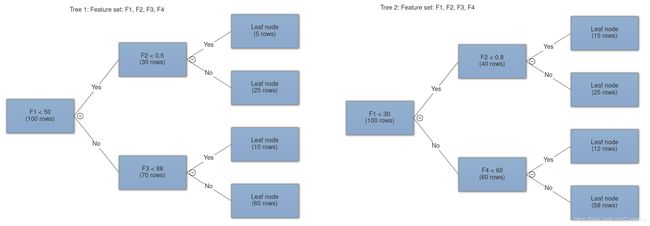
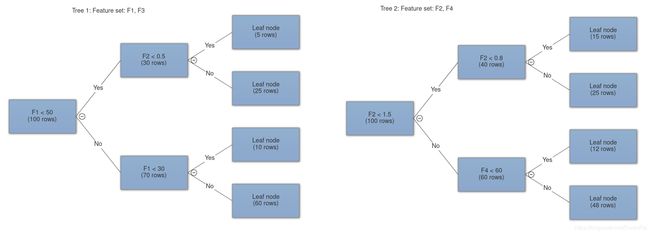
1.特征bagging：自举过程是一种从原始样本中进行又放回的采样。在特征 bagging 过程中，我们从原始特征中进行随机特征采样，并且把采样到的特征传递到不同的树上面。（不采用放回的采集，因为具有冗余特征是没有意义的）。这样做事为了减少树之间的相关性。我们的目标就是制作高度不相关的决策树。

2.聚合：使随机森林比决策树更好的核心是聚合不相关的树。我们的想法是创建几个浅层的树模型，然后将它们平均化以创建更好的随机森林，这样可以将一些随机误差的平均值变为零。在回归的情况下，我们可以平均每个树的预测（平均值），而在分类问题的情况下，我们可以简单的取每个树投票的大多数类别。

Python 代码

要从头开始编码我们的随机森林，我们将遵循自上而下的方法。我们将从一个黑盒子开始，并进一步将其分解为几个黑盒子，抽象级别越来越低，细节越来越多，直到我们最终达到不再抽象的程度。

随机森林类

我们正在创建一个随机森林回归器，如果你想创建一个分类器，那么只需要对此代码进行细微的调整就行了。首先，我们需要知道我们的黑盒子的输入和输出是什么，所以我们需要知道定义我们的随机森林的参数是：

• x：训练集的自变量。为了保持简单，我不单独创建一个 fit 方法，因此基类构造函数将接受训练集；
• y：监督学习所需的相应因变量（随机森林是一种监督学习技术）；
• n_trees：我们合作创建随机森林的不相关树的数量；
• n_features：要采样并传递到每棵树的要素数量，这是特征bagging 发生的位置。它可以是 sqrt ，log2 或者整数。在 sqrt 的情况下，对于每个树采样的特征的数量是总特征的平方根，在 log2 的情况下是总特征的对数基数 2；
• sample_size：随机选择并传递到每个树的行数。这通常等于总行数，但在某些情况下可以减少以提高性能并降低树的相关性（树的 bagging 方法是一种完全独立的机器学习技术）；
• depth：每个决策树的深度。更高的深度意味着更多的分裂，这增加了每棵树的过度拟合倾向，但由于我们聚集了几个不相关的树木，所以过度拟合单个树木几乎不会对整个森林造成干扰；
• min_leaf：节点中导致进一步拆分所需的最小行数。降低 min_leaf，树的深度会越高；

让我们开始定义我们的随机森林类。

class RandomForest():
    def __init__(self, x, y, n_trees, n_features, sample_sz, depth=10, min_leaf=5):
        np.random.seed(12)
        if n_features == 'sqrt':
            self.n_features = int(np.sqrt(x.shape[1]))
        elif n_features == 'log2':
            self.n_features = int(np.log2(x.shape[1]))
        else:
            self.n_features = n_features
        print(self.n_features, "sha: ",x.shape[1])    
        self.x, self.y, self.sample_sz, self.depth, self.min_leaf  = x, y, sample_sz, depth, min_leaf
        self.trees = [self.create_tree() for i in range(n_trees)]

    def create_tree(self):
        idxs = np.random.permutation(len(self.y))[:self.sample_sz]
        f_idxs = np.random.permutation(self.x.shape[1])[:self.n_features]
        return DecisionTree(self.x.iloc[idxs], self.y[idxs], self.n_features, f_idxs,
                    idxs=np.array(range(self.sample_sz)),depth = self.depth, min_leaf=self.min_leaf)
        
    def predict(self, x):
        return np.mean([t.predict(x) for t in self.trees], axis=0)

def std_agg(cnt, s1, s2): return math.sqrt((s2/cnt) - (s1/cnt)**2)

• __init__：构造函数只需借助我们的参数定义随机森林并创建所需数量的树；
• creat_tree：通过调用 Decision Tree 类的构造函数创建一个新的决策树。现在假设它是一个黑盒子。我们稍后会写关于它的代码。每棵树都会受到一个随机的特征子集（特征 bagging）和一组随机的行；
• Predict：我们的随机森林预测只是所有决策树预测的平均值；

如果我们能够神奇的创建树，那么想想随机森林是多么容易。现在我们降低抽象级别并编写代码来创建决策树。

决策树类

决策树将具有以下参数：

• indxs：此参数用于跟踪原始集的哪些索引向右移动，哪些索引转到左侧树。因此，每个树都有这个参数 indxs，它存储它包含的行的索引。通过平均这些行来进行预测。
• min_leaf：叶节点上需要的最小行样本。每个叶节点的行样本都小于 min_leaf ，因为它们不能再分割。
• depth：每棵树内可能的最大深度或者最大分割数。

class DecisionTree():
    def __init__(self, x, y, n_features, f_idxs,idxs,depth=10, min_leaf=5):
        self.x, self.y, self.idxs, self.min_leaf, self.f_idxs = x, y, idxs, min_leaf, f_idxs
        self.depth = depth
        self.n_features = n_features
        self.n, self.c = len(idxs), x.shape[1]
        self.val = np.mean(y[idxs])
        self.score = float('inf')
        self.find_varsplit()
        
    def find_varsplit(self):
        #Will make it recursive later
        for i in self.f_idxs: self.find_better_split(i)
       

    def find_better_split(self, var_idx):
        #Lets write it later
        pass
    

        for i in range(0,self.n-self.min_leaf-1):
            xi,yi = sort_x[i],sort_y[i]
            lhs_cnt += 1; rhs_cnt -= 1
            lhs_sum += yi; rhs_sum -= yi
            lhs_sum2 += yi**2; rhs_sum2 -= yi**2
            if i<self.min_leaf or xi==sort_x[i+1]:
                continue

            lhs_std = std_agg(lhs_cnt, lhs_sum, lhs_sum2)
            rhs_std = std_agg(rhs_cnt, rhs_sum, rhs_sum2)
            curr_score = lhs_std*lhs_cnt + rhs_std*rhs_cnt
            if curr_score<self.score: 
                self.var_idx,self.score,self.split = var_idx,curr_score,xi

    @property
    def split_name(self): return self.x.columns[self.var_idx]
    
    @property
    def split_col(self): return self.x.values[self.idxs,self.var_idx]

    @property
    def is_leaf(self): return self.score == float('inf') or self.depth <= 0 
    

    def predict(self, x):
        return np.array([self.predict_row(xi) for xi in x])

    def predict_row(self, xi):
        if self.is_leaf: return self.val
        t = self.lhs if xi[self.var_idx]<=self.split else self.rhs
        return t.predict_row(xi)

我们使用属性装饰器使我们的代码更加简洁。

• __init__：决策树构造函数。它有几个有趣的片段可供研究：

a. 如果 idxs 为 None：idxs = np.arange(len(y))，如果我们没有在这个特定树的计算中指定行的索引，只需占用所有行；

b. self.val = np.mean(y[idxs]) 每个决策树预测一个值，该值是它所持有的所有行的平均值。变量 self.val 保存树的每个节点的预测。对于根节点，该值将仅仅是所有观察值的平均值，因为它保留了所有行，因为我们尚未进行拆分。我在这里使用了“节点”这个词，因为本质上决策树只是一个节点，左边是决策树，右边也是决策树。

c. Self.score = float(“inf”) 节点的得分是根据它如何 “划分” 原始数据集来进行计算的。我们稍后会定义这个 “好”，我们现在假设我们有办法测量这样的数量。此外，我们的节点将得分设置为无穷大，因为我们尚未进行任何拆分，因此我们存在的拆分无线差，表明任何拆分都优于不拆分。

d. self.find_varsplit() 我们首先进行拆分！

• find_varsplit：我们使用暴力方法找到最佳分裂。此函数按顺序循环遍历所有列，并在他们之间找到最佳分割。这个函数仍然不完整，因为它只进行一次拆分，后来我们扩展这个函数，为每个拆分做出左右决策，直到我们到达叶子节点。
• split_name：一个属性装饰器，用于返回我们要拆分的列的名称。var_idx 是此列的索引，我们将在 find_better_split 函数中计算此索引以及我们拆分的列的值。
• split_col：一个属性装饰器，用于返回索引 var_idx 处的列，其中元素位于 indxs 变量给出的索引处。基本上，将列与选定的行隔离。
• find_better_split：这个函数是在某个列中找到最好的分割，这很复杂，所以我们在上面的代码中把它看做是一个黑盒子。让我们稍后再定义它。
• is_leaf：叶节点是从未进行过分割的节点，因此它具有无限分数，因此该函数用于标识叶节点。同样，如果我们已经越过了最大深度，即 self.depth <= 0 ，它就是一个叶子节点，因为我们不能再深入了。

如何找到最好的分割点？

决策树通过基于某些条件递归的将数据分为两半来进行训练。如果测试集在每列中有 10 列，每列有 10 个数据点，则总共可以进行 10*10 = 100 次拆分，我们手头的任务是找到哪些拆分是最适合我们的数据。

我们根据将数据分为两半，然后使得两者中的每一个数据都是非常“相似的”。增加这种相似性的一种方法是减少两半的方差或者标准偏差。因此，我们希望最小化两边标准差的加权平均值。我们使用贪婪算法通过将数据划分为列中每个值的两半来找到拆分，并计算两半的标准偏差的加权平均值以找到最小值。

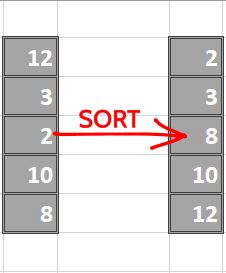
为了加快速度，我们可以复制一个列并对其进行排序，通过在第 n+1 个索引处使用 sum 的值和由第 n 个索引分割创建的两半值的平方和来分割加权平均值来计算加权平能均值。这是基于以下标准偏差公式：

下面的图像以图形方式展示了分数计算的过程，每个图像中的最后一列是表示分割得分的单个数字，即左右标准偏差的加权平均值。

我们继续对每列进行排序：

现在我们按顺序进行拆分：

index = 0

index = 1

Index = 2 (best split)

Index = 3

index = 4

index=5

通过简单的贪婪算法，我们发现在 index = 2 时进行的拆分是最好的拆分，因为它得分最低。我们稍后对所有列执行相同的步骤并将它们全部比较以贪婪算法找到最小值。

以下是上述图示表示的简单代码：

def std_agg(cnt, s1, s2): return math.sqrt((s2/cnt) - (s1/cnt)**2)
 
 def find_better_split(self, var_idx):
        x, y = self.x.values[self.idxs,var_idx], self.y[self.idxs]
        sort_idx = np.argsort(x)
        sort_y,sort_x = y[sort_idx], x[sort_idx]
        rhs_cnt,rhs_sum,rhs_sum2 = self.n, sort_y.sum(), (sort_y**2).sum()
        lhs_cnt,lhs_sum,lhs_sum2 = 0,0.,0.

        for i in range(0,self.n-self.min_leaf-1):
            xi,yi = sort_x[i],sort_y[i]
            lhs_cnt += 1; rhs_cnt -= 1
            lhs_sum += yi; rhs_sum -= yi
            lhs_sum2 += yi**2; rhs_sum2 -= yi**2
            if i<self.min_leaf or xi==sort_x[i+1]:
                continue

            lhs_std = std_agg(lhs_cnt, lhs_sum, lhs_sum2)
            rhs_std = std_agg(rhs_cnt, rhs_sum, rhs_sum2)
            curr_score = lhs_std*lhs_cnt + rhs_std*rhs_cnt
            if curr_score<self.score: 
                self.var_idx,self.score,self.split = var_idx,curr_score,xi

上面的代码我们需要一些解释：

• 函数 std_agg 使用平方和的值来计算标准偏差；
• curr_score = lhs_std*lhs_cnt + rhs_std*rhs_cnt 每次迭代的分割得分只是两个标准差的加权平均值。较低的分数有助于降低方差，较低的方差有助于对类似数据进行分组，从而实现更好的预测；
• if curr_score

现在我们知道如何为所选列找到最佳拆分，我们需要递归的为每个决策树进行拆分。对于每一棵树，我们找到最好的列和它的值，然后我们递归的制作两个决策树，知道我们到达叶子及诶单。为此，我们将不完整的函数 find_varsplit 进行扩展：

def find_varsplit(self):
        for i in self.f_idxs: self.find_better_split(i)
        if self.is_leaf: return
        x = self.split_col
        lhs = np.nonzero(x<=self.split)[0]
        rhs = np.nonzero(x>self.split)[0]
        lf_idxs = np.random.permutation(self.x.shape[1])[:self.n_features]
        rf_idxs = np.random.permutation(self.x.shape[1])[:self.n_features]
        self.lhs = DecisionTree(self.x, self.y, self.n_features, lf_idxs, self.idxs[lhs], depth=self.depth-1, min_leaf=self.min_leaf)
        self.rhs = DecisionTree(self.x, self.y, self.n_features, rf_idxs, self.idxs[rhs], depth=self.depth-1, min_leaf=self.min_leaf)

完结

最后我们给出完整代码：

class RandomForest():
    def __init__(self, x, y, n_trees, n_features, sample_sz, depth=10, min_leaf=5):
        np.random.seed(12)
        if n_features == 'sqrt':
            self.n_features = int(np.sqrt(x.shape[1]))
        elif n_features == 'log2':
            self.n_features = int(np.log2(x.shape[1]))
        else:
            self.n_features = n_features
        print(self.n_features, "sha: ",x.shape[1])    
        self.x, self.y, self.sample_sz, self.depth, self.min_leaf  = x, y, sample_sz, depth, min_leaf
        self.trees = [self.create_tree() for i in range(n_trees)]

    def create_tree(self):
        idxs = np.random.permutation(len(self.y))[:self.sample_sz]
        f_idxs = np.random.permutation(self.x.shape[1])[:self.n_features]
        return DecisionTree(self.x.iloc[idxs], self.y[idxs], self.n_features, f_idxs,
                    idxs=np.array(range(self.sample_sz)),depth = self.depth, min_leaf=self.min_leaf)
        
    def predict(self, x):
        return np.mean([t.predict(x) for t in self.trees], axis=0)

def std_agg(cnt, s1, s2): return math.sqrt((s2/cnt) - (s1/cnt)**2)

class DecisionTree():
    def __init__(self, x, y, n_features, f_idxs,idxs,depth=10, min_leaf=5):
        self.x, self.y, self.idxs, self.min_leaf, self.f_idxs = x, y, idxs, min_leaf, f_idxs
        self.depth = depth
        print(f_idxs)
#         print(self.depth)
        self.n_features = n_features
        self.n, self.c = len(idxs), x.shape[1]
        self.val = np.mean(y[idxs])
        self.score = float('inf')
        self.find_varsplit()
        
    def find_varsplit(self):
        for i in self.f_idxs: self.find_better_split(i)
        if self.is_leaf: return
        x = self.split_col
        lhs = np.nonzero(x<=self.split)[0]
        rhs = np.nonzero(x>self.split)[0]
        lf_idxs = np.random.permutation(self.x.shape[1])[:self.n_features]
        rf_idxs = np.random.permutation(self.x.shape[1])[:self.n_features]
        self.lhs = DecisionTree(self.x, self.y, self.n_features, lf_idxs, self.idxs[lhs], depth=self.depth-1, min_leaf=self.min_leaf)
        self.rhs = DecisionTree(self.x, self.y, self.n_features, rf_idxs, self.idxs[rhs], depth=self.depth-1, min_leaf=self.min_leaf)

    def find_better_split(self, var_idx):
        x, y = self.x.values[self.idxs,var_idx], self.y[self.idxs]
        sort_idx = np.argsort(x)
        sort_y,sort_x = y[sort_idx], x[sort_idx]
        rhs_cnt,rhs_sum,rhs_sum2 = self.n, sort_y.sum(), (sort_y**2).sum()
        lhs_cnt,lhs_sum,lhs_sum2 = 0,0.,0.

        for i in range(0,self.n-self.min_leaf-1):
            xi,yi = sort_x[i],sort_y[i]
            lhs_cnt += 1; rhs_cnt -= 1
            lhs_sum += yi; rhs_sum -= yi
            lhs_sum2 += yi**2; rhs_sum2 -= yi**2
            if i<self.min_leaf or xi==sort_x[i+1]:
                continue

            lhs_std = std_agg(lhs_cnt, lhs_sum, lhs_sum2)
            rhs_std = std_agg(rhs_cnt, rhs_sum, rhs_sum2)
            curr_score = lhs_std*lhs_cnt + rhs_std*rhs_cnt
            if curr_score<self.score: 
                self.var_idx,self.score,self.split = var_idx,curr_score,xi

    @property
    def split_name(self): return self.x.columns[self.var_idx]
    
    @property
    def split_col(self): return self.x.values[self.idxs,self.var_idx]

    @property
    def is_leaf(self): return self.score == float('inf') or self.depth <= 0 
    

    def predict(self, x):
        return np.array([self.predict_row(xi) for xi in x])

    def predict_row(self, xi):
        if self.is_leaf: return self.val
        t = self.lhs if xi[self.var_idx]<=self.split else self.rhs