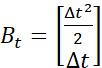卡尔曼滤波的原理(Python实现)
我们假设有一辆运动的汽车,要跟踪汽车的位置 p 和速度 v,这两个变量称为状态变量,我们使用状态变量矩阵 ![]() 来表示小车在 t 时刻的状态,那么在经过 Δt 的时间之后,当前时刻的位置和速度分别为:
来表示小车在 t 时刻的状态,那么在经过 Δt 的时间之后,当前时刻的位置和速度分别为:
其中 ![]() 表示 t 时刻的加速度大小,由于卡尔曼滤波只能描述状态与状态之间的线性关系,所以可将上述两个表达式转换为矩阵向量的形式为:
表示 t 时刻的加速度大小,由于卡尔曼滤波只能描述状态与状态之间的线性关系,所以可将上述两个表达式转换为矩阵向量的形式为:
![]() (式1.4)
(式1.4)
式l.4就是卡尔曼滤波器的第一个公式——状态预测公式,其中F称为状态转移矩阵,表示我们如何从上一状态推测出当前状态;B表示控制矩阵,表示控制量u对当前状态的影响;x头上之所以加一个^表示它是一个估计值,而不是真实值,而-上标表示这并非最佳估计。
用协方差矩阵表示预测的不确定性,比如对二维的噪声,x方向满足高斯分布,y方向也满足高斯分布,而这两个方向的高斯分布是可能存在相关性的,所以我们需要引入协方差矩阵。
正对角线上的值表示的是两个维度噪声各自的方差,反对角线上的两个值是相等的,表示的是两个维度噪声的协方差。
噪声协方差矩阵对系统会产生影响,所以我们要传递到系统中去,这时候噪声协方差矩阵要乘以状态转移矩阵F,于是我们得到式1.6。
![]() (式1.6)
(式1.6)
这里我们用到了协方差矩阵的性质 ![]() 。而由于我们的模型肯定是存在误差的,所以我们要加入表示误差的矩阵Q。
。而由于我们的模型肯定是存在误差的,所以我们要加入表示误差的矩阵Q。
![]() (式1.7)
(式1.7)
式1.7就是卡尔曼滤波器的第二个公式——表示不确定性在各个时刻之间的传递关系。
假设我们通过一个距离传感器测量小车的位置记为 ![]() ,由于我们的状态变量是一个二维矩阵,而表示距离的
,由于我们的状态变量是一个二维矩阵,而表示距离的 ![]() 是一个标量,所以状态变量矩阵就要乘以一个观测矩阵H,当然我们观测到的位置也不一定是绝对准确的,所以也要加上一个观测噪声v,得到式1.8。
是一个标量,所以状态变量矩阵就要乘以一个观测矩阵H,当然我们观测到的位置也不一定是绝对准确的,所以也要加上一个观测噪声v,得到式1.8。
![]() (式1.8)
(式1.8)
同样,观测噪声的协方差矩阵我们用R来表示。这里我们只采用了一种测量方式得到汽车的位置,而实际中我们可能通过多种方式来得到小车的观测位置,这时候 ![]() 就不是一个标量,而是多个观测值组成的矩阵,而每一个观测值都是真实状态的一种不完全的表现,我们就可以从这些不完整观测值推断小车的真实位置。
就不是一个标量,而是多个观测值组成的矩阵,而每一个观测值都是真实状态的一种不完全的表现,我们就可以从这些不完整观测值推断小车的真实位置。
通过距离传感器,我们得到了位置观测值 ![]() 和观测噪声的协方差矩阵R,现在我们需要将观测得到的这些值融入到状态向量中,如式1.9所示。
和观测噪声的协方差矩阵R,现在我们需要将观测得到的这些值融入到状态向量中,如式1.9所示。
![]() (式1.9)
(式1.9)
在式1.4中我们得到了非最佳估计 ![]() ,然后我们将观测得到的值加到它的后面就得到了最佳估计
,然后我们将观测得到的值加到它的后面就得到了最佳估计 ![]() 。我们在(式1.9)增加的内容中,
。我们在(式1.9)增加的内容中,![]() 表示我们实际的观测值和预测值之间的残差,残差乘上系数K就可以用来修正
表示我们实际的观测值和预测值之间的残差,残差乘上系数K就可以用来修正 ![]() 的值。这个K就是卡尔曼系数,表示为:
的值。这个K就是卡尔曼系数,表示为:
![]() (式1.10)
(式1.10)
卡尔曼系数的作用主要有两个方面:
第一是权衡预测状态协方差矩阵P和观察量协方差矩阵R的大小,来决定我们是相信预测模型多一点还是观察模型多一点。如果相信预测模型多一点,这个残差的权重就会小一点,如果相信观察模型多一点,权重就会大一点。
第二就是把残差的表现形式从观察域转换到状态域,在我们这个例子中,观察值z表示的是小车的位置,只是一个一维向量,而状态向量是一个二维向量,它们所使用的单位和描述的特征都是不同的。而卡尔曼系数就是要实现这样将一维的观测向量转换为二维的状态向量的残差,在本例中我们只观测了小车的位置,而在K中已经包含了协方差矩阵P的信息,所以就利用了位置和速度这两个维度的相关性,从位置的信息中推测出了速度的信息,从而让我们可以对状态量x的两个维度同时进行修正。
最后,我们还要对噪声协方差进行更新,用于下一次迭代,可以表示为:
![]() (式1.11)
(式1.11)
在这一轮里噪声的不确定性是减小的,而在下一轮迭代中,由于传递噪声的引入,不确定性又会增大,卡尔曼滤波器就是在这种不确定性的变化中寻求一种平衡。
综上所述,我们得到了卡尔曼滤波器的5个公式如下:
![]() ①
①
![]() ②
②
![]() ③
③
![]() ④
④
![]() ⑤
⑤
前两个表示的是根据上一时刻的状态来预测当前时刻的状态,通过这两个公式我们得到的是非最佳估计的x和P;后三个公式就是通过当前的观测值来更新x和P,更新之后的就是最佳观测值。
下面是我用Python简单模拟预测小车位置和速度的一段程序,观测的值是一段从0到99,速度为1的匀速行驶路径,加入的噪声是均值为0,方差为1的高斯噪声。
import numpy as np
import matplotlib.pyplot as plt
# 创建一个0-99的一维矩阵
z = [i for i in range(100)]
z_watch = np.mat(z)
#print(z_mat)
# 创建一个方差为1的高斯噪声,精确到小数点后两位
noise = np.round(np.random.normal(0, 1, 100), 2)
noise_mat = np.mat(noise)
# 将z的观测值和噪声相加
z_mat = z_watch + noise_mat
#print(z_watch)
# 定义x的初始状态
x_mat = np.mat([[0,], [0,]])
# 定义初始状态协方差矩阵
p_mat = np.mat([[1, 0], [0, 1]])
# 定义状态转移矩阵,因为每秒钟采一次样,所以delta_t = 1
f_mat = np.mat([[1, 1], [0, 1]])
# 定义状态转移协方差矩阵,这里我们把协方差设置的很小,因为觉得状态转移矩阵准确度高
q_mat = np.mat([[0.0001, 0], [0, 0.0001]])
# 定义观测矩阵
h_mat = np.mat([1, 0])
# 定义观测噪声协方差
r_mat = np.mat([1])
for i in range(100):
x_predict = f_mat * x_mat
p_predict = f_mat * p_mat * f_mat.T + q_mat
kalman = p_predict * h_mat.T / (h_mat * p_predict * h_mat.T + r_mat)
x_mat = x_predict + kalman *(z_mat[0, i] - h_mat * x_predict)
p_mat = (np.eye(2) - kalman * h_mat) * p_predict
plt.plot(x_mat[0, 0], x_mat[1, 0], 'ro', markersize = 1)
plt.show()
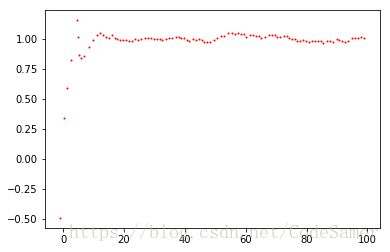
运行结果如下:
横坐标表示离初始位置的距离p,纵坐标表示在该位置的速度v。可以发现,开始时预测值和实际值有较大出入,在经过一段很短的时间后,速度预测值与实际值1基本就很接近了!
以上就是本人最近在学习卡尔曼滤波时的一些收获,由于本人之前也是小白,所以有不正确的地方欢迎指正,谢谢!