Pinball HDU - 6373（物理题）

Pinball HDU - 6373

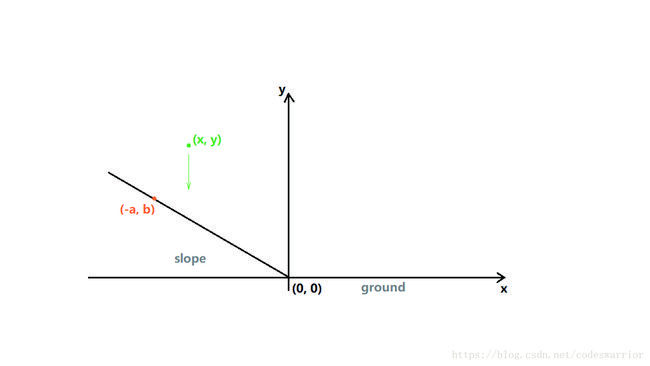
There is a slope on the 2D plane. The lowest point of the slope is at the origin. There is a small ball falling down above the slope. Your task is to find how many times the ball has been bounced on the slope.

It’s guarantee that the ball will not reach the slope or ground or Y-axis with a distance of less than 1 from the origin. And the ball is elastic collision without energy loss. Gravity acceleration g=9.8m/s2.

Input
There are multiple test cases. The first line of input contains an integer T (1 ≤ T ≤ 100), indicating the number of test cases.

The first line of each test case contains four integers a, b, x, y (1 ≤ a, b, -x, y ≤
100), indicate that the slope will pass through the point(-a, b), the initial position of the ball is (x, y).
Output
Output the answer.

It's guarantee that the answer will not exceed 50.

Sample Input

1
5 1 -5 3

Sample Output

2

题意：

给定斜面的上一点坐标(a,b)，和小球初始下落位置（x,y），问小球在斜面上一共弹了多少次，小球是弹性碰撞没有能量损失

分析：

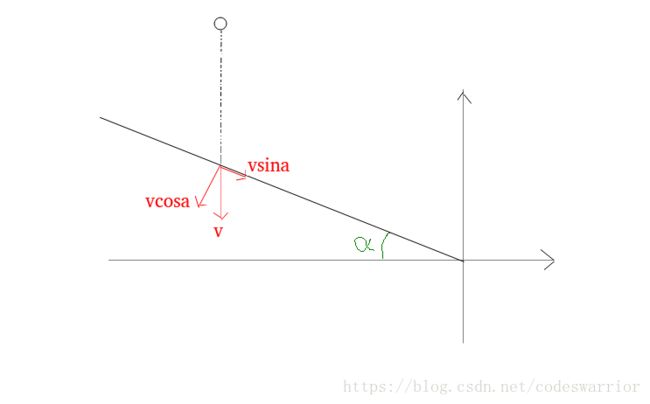
将小球第一次碰到斜面时的速度分解成垂直于斜面和平行于斜面的两个分速度

平行于斜面的速度以及加速度： vx=2gh−−−√sinα    gx=gsinα v x = 2 g h s i n α         g x = g s i n α

垂直于斜面的速度以及加速度： vy=2gh−−−√cosα    gy=gcosα v y = 2 g h c o s α         g y = g c o s α

两次碰撞的时间间隔：

实际上计算两次碰撞间隔时间我们只需要考虑垂直于斜面方向的速度即可，因为平行于斜面的速度是不断增加的，而垂直于斜面的速度在两次碰撞的间隔中它的变化是 vy→0→vy v y → 0 → v y 并且加速度不变都是 gcosα g c o s α

因此间隔时间 t=2vygy=22gh√cosαgcosα=22gh√g t = 2 v y g y = 2 2 g h c o s α g c o s α = 2 2 g h g

第一次碰撞后的位移：

x1=vxt+12gxt2=4hsinα+4hsinα=8hsinα x 1 = v x t + 1 2 g x t 2 = 4 h s i n α + 4 h s i n α = 8 h s i n α

第二次碰撞后，平行于斜面的速度变为

v′x=vx+gxt=2gh−−−√sinα+gsinα⋅22gh√g=32gh−−−√sinα v x ′ = v x + g x t = 2 g h s i n α + g s i n α ⋅ 2 2 g h g = 3 2 g h s i n α

因此我们依然可以再次算出碰撞第二次后的沿斜面的位移：

x2=v′xt+12gxt2=32gh−−−√sinα⋅22gh√g+12gsinα4×2ghg=12hsinα x 2 = v x ′ t + 1 2 g x t 2 = 3 2 g h s i n α ⋅ 2 2 g h g + 1 2 g s i n α 4 × 2 g h g = 12 h s i n α
.
.
.
因此我们可以推出小球沿斜面的位移之比为1:2:3:4:5…..

而第一次的位移为 8hsinα 8 h s i n α

因此直接循环判断即可

code：

#include 
using namespace std;
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        double a,b,x,y;
        scanf("%lf%lf%lf%lf",&a,&b,&x,&y);
        double angle = atan(b / a);
        double sinn = sin(angle);
        double h = y - b / a * (-x);//小球第一次落点斜面高度
        double L = (y - h) / sinn;//小球第一次落点斜面长度
        int ans = 0,sum = 0;
        for(int i = 1; i <= 50; i++){
            ans++;
            sum += i;
            if((double)sum*8.0*h*sinn > L){
                printf("%d\n",ans);
                break;
            }
        }
    }
    return 0;
}