计算几何判断线段相交+计数并查集HDU1558

                                           Segment set

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5413    Accepted Submission(s): 2087
Problem Description

A segment and all segments which are connected with it compose a segment set. The size of a segment set is the number of segments in it. The problem is to find the size of some segment set.

Input

In the first line there is an integer t - the number of test case. For each test case in first line there is an integer n (n<=1000) - the number of commands. 

There are two different commands described in different format shown below:

P x1 y1 x2 y2 - paint a segment whose coordinates of the two endpoints are (x1,y1),(x2,y2).
Q k - query the size of the segment set which contains the k-th segment.

k is between 1 and the number of segments in the moment. There is no segment in the plane at first, so the first command is always a P-command.

Output

For each Q-command, output the answer. There is a blank line between test cases.

Sample Input

1

10

P 1.00 1.00 4.00 2.00

P 1.00 -2.00 8.00 4.00

Q 1

P 2.00 3.00 3.00 1.00

Q 1

Q 3

P 1.00 4.00 8.00 2.00

Q 2

P 3.00 3.00 6.00 -2.00

Q 5

Sample Output

1

2

2

2

5

题意比较好理解，增加一条线段，若果和已有的线段相交，则把他们加入到一个集合中，对于每个问讯，输出这条线段所在集合的元素个数；

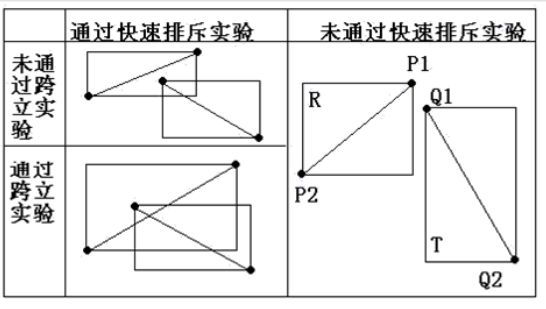
思路：快速排斥跨立实验判断相交，计数并查集维护集合合并；

排斥实验的要点： 

bool quick(double x1,double  y1,double x2,double y2,double x3,double y3,double x4,double y4)
{
    if(min(x1,x2)>max(x3,x4)) return false;
    if(max(x1,x2)max(y3,y4)) return false;
    if(max(y1,y2)

 排斥实验和跨立实验缺一不可

跨立实验要点：1，差集相乘的符号；2，必须要判断两次（两条线段交换判断）

ac代码：

#include
#include
#include
#include
using namespace std;
int vis[100010];
int t;
int n;
int tot;
struct site
{
    double x,y;
};
struct segment
{
    site l,r;
    int no;
}a[1005];
int pre[1005];
int cnt[1005];

int find(int x)
{
    int rt=x;
    while(rt!=pre[rt])
    {
        rt=pre[rt];
    }
    int i=x;
    while(i!=pre[i])
    {
        int fa=pre[i];
        pre[i]=rt;
        i=fa;
    }
    return rt;
}

bool quick(double x1,double  y1,double x2,double y2,double x3,double y3,double x4,double y4)
{
    if(min(x1,x2)>max(x3,x4)) return false;
    if(max(x1,x2)max(y3,y4)) return false;
    if(max(y1,y2)