数学建模(三) 预测与评价
预测和评价
预测和评价这一节的话范围比较大,可介绍的方法也比较多,边写边学吧。
评价模型
1.加权平均
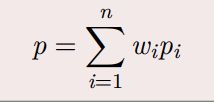
例:cumcm2011B:
5.2问题二:
5.2.1对交巡警服务平台设置方案的合理性研究
(1)首先建立线性加权评价模型来分析评价该市交巡警服务平台设置方案的合理性。
根据第一问第一个子问题的模型,对六个区和全市可分别求出服务平台的覆盖率和平均每个服务平台工作强度的方差。确定两个评价指标,分别是各个区的服务平台覆盖率以及各个服务平台的工作强度。设各个区和全市的服务平台覆盖率为g,做归一化处理后的数据为gn ;各个区内服务平台工作强度的方差为s,方差的倒数1/s,做归一化处理后的数据为vn。那么综合评价指标h为
h=a*gn+(1-a)*vn
其中,a为权重系数,a属于0到1。
2.层次分析
这个方法由于很多教程都提到了,我就略仔细写一下。
首先是建立一个层次结构模型。
然后对属性值(下图准则层)生成一个判断矩阵A,Aij代表属性i相对于j的重要性,7就代表i比j重要非常非常多,1/7则相反。这个矩阵完全是自己定义的,感觉自己权力很大有没有,没有,因为要查文献的,不能乱给。
然后依次是层次单排序及一致性检验,层次多排序及一致性检验。

层次单排序:
disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>p
i=i+1;
x(:,i)=A*y(:,i-1);
m(i)=max(x(:,i));
y(:,i)=x(:,i)/m(i);
k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
%一致性指标
CR=CI/RI(n); %一致性比例
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
end
请输入判断矩阵A(n阶)
A=[1 1/2 4 3 3;2 1 7 5 5;1/4 1/7 1 1/2 1/3;1/3 1/5 2 1 1;1/3 1/5 3 1 1];
0.2636
0.4758
0.0538
0.0981
0.1087
此矩阵的一致性可以接受!
CI=
0.0180
CR=
0.0161
输出为准则层权重,一个包含层次总排序的如下,A1-A4其实是方案层针对准则层每个点有一个矩阵,规则如上,最后会得到一个最终的权值:
function ahpactor
A = [1/1 2/1 5/1 3/1
1/2 1/1 3/1 1/2
1/5 1/3 1/1 1/4
1/3 2/1 4/1 1/1];
[w, CR] = AHP(A);
% face
A1 = [1/1 1/2 3/1
2/1 1/1 5/1
1/3 1/5 1/1];
[w1, CR1] = AHP(A1);
% body
A2 = [1/1 1/3 2/1
3/1 1/1 5/1
1/2 1/5 1/1];
[w2, CR2] = AHP(A2);
% voice
A3 = [1/1 2/1 1/5
1/2 1/1 1/7
5/1 7/1 1/1];
[w3, CR3] = AHP(A3);
% acting
A4 = [1/1 2/1 1/3
1/2 1/1 1/5
3/1 5/1 1/1];
[w4, CR4] = AHP(A4);
CRs = [CR1 CR2 CR3 CR4]
P = [w1 w2 w3 w4] * w
% ------------------------------------------------------------------------
function [w, CR] = AHP(A)
% n= [ 1 2 3 4 5 6 7 8 9
RI = [ 0.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45];
n = size(A,1);
[V, D] = eig(A);
[lamda, i] = max(diag(D));
CI=(lamda-n)/(n-1);
CR = CI/RI(n);
W = V(:,i);
w = W/sum(W);
3.模糊综合评价
这一part就不得不说到扎德,模糊集和隶属函数。不还是不说了,应用起来可以不搞那么复杂,一张图:

W是权重,R是投票矩阵,其中横坐标是属性,纵坐标是每个投票人投的票数,每一行总和为1,可以看到权值和也是1。
一段代码:
W = [0.4 0.2 0.1 0.3];
R = [0.38 0.34 0.17 0.11 0.00
0.26 0.41 0.20 0.13 0.00
0.27 0.23 0.21 0.15 0.14
0.14 0.19 0.22 0.12 0.33];
% B = max(R .* W')
B = max(R .* repmat(W',1,size(R,2)) )
例:NPMCM2017E:
第四问:道路节点受到攻击破坏会延迟甚至阻碍发射装置按时到达指定发射点位。请结合图1路网特点,考虑攻防双方的对抗博弈,建立合理的评价指标,量化分析该路网最可能受到敌方攻击破坏的3个道路节点。
先略到这
预测模型
1.拟合
这里说一下拟合和回归的区别,拟合并不特指某一种方法,指的是对一些数据,按其规律方程化,而其方程化的方法有很多,回归只是其中一种方法,还有指数平滑这样简单一些的方法,或者ARIMA,VAR,等等各种复杂一点的方法。拟合是一种数据处理的方式,不特指哪种方法。简单的说就是你有一组数据,觉得这组数据和一个已知的函数(这个函数的参数未定)很相似,为了得到最能表示这组数据特征的这个函数,通过拟合这种方式(具体的数学方法很多)求得参数。也有些拟合得到的参数并非是函数的参数,如神经网络,得到的是这个神经网络的参数。
总的来说,回归是拟合的一种方法。拟合的概念更广泛,拟合包含回归,还包含插值和逼近。回归强调有随机因素,而拟合没有。拟合侧重于调整曲线的参数,使得与数据相符。而回归重在研究两个变量或多个变量之间的关系。
函数可用polyfit()和fit()。
polyfit()多项式拟合,一个小例子:
x0=[1990 1991 1992 1993 1994 1995 1996];
y0=[70 122 144 152 174 196 202];
a=polyfit(x0,y0,1)
y97=polyval(a,1997)
y98=polyval(a,1998)
有时候涉及到自己拟合自己编写的函数,比如自己创建一个函数模型,然后需要数据来拟合模型的未知参数,这些都可以fit解决。例:
[f,e,out]=fit([x,y],imv,‘youfun1(x,y,p1,p2,g)’,‘StartPoint’,[50 0.03]);
1.2 插值
把插值放在这里主要是和拟合有些相似的地方,插值:求过已知有限个数据点的近似函数。拟合:已知有限个数据点,求近似函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最小。
比较常用的是分段线性插值:简单地说,将每两个相邻的节点用直线连起来,如此形成的一条折线就是分段线性插值函数,记作 In (x) ,它满足 In (xi ) = yi ,且 In (x) 在每个小区间[xi , xi+1]上是线性。
一维插值函数:y=interp1(x0,y0,x,‘method’)
method 指定插值的方法,默认为线性插值。其值可为:
‘nearest’ 最近项插值;‘linear’ 线性插值;‘spline’ 逐段 3 次样条插值;‘cubic’ 保凹凸性 3 次插值(默认为线性插值)。所有的插值方法要求 x0 是单调的。
当 x0 为等距时可以用快速插值法,使用快速插值法的格式为:’*nearest’、’*linear’、’*spline’、 ‘*cubic’。
2.时间序列
时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序
列的方法构成数据分析的一个重要领域,即时间序列分析。
时序预测:根据时序过去的变化规律,推测今后趋势。
时间序列的变化形式:长期趋势变动 Tt;季节变动 St;循环变动 Ct;
不规则变动 Rt
模型:加法,乘法,混合模型
一次移动平均法:
y = [533.8 574.6 606.9 649.8 705.1, ...
772.0 816.4 892.7 963.9 1015.1];
m = length(y);
n = 4;
c = cumsum(y);
yhat = ( c(n:end)-[0 c(1:end-n)] )/n;
S = norm(yhat(1:end-1) - y(n+1:end))/sqrt(m-n) %标准差
还有指数平滑法,差分指数平滑法等。
3.灰色预测
灰色预测模型(Gray Forecast Model)是通过少量的、不完全的信息,建立数学模型并做出预测的一种预测方法。
特点:
模型使用的不是原始数据,而是生成数据。
不需要很多数据,一般只需 ≥ 4 个数据。
只适用于中短期的预测,只适合指数增长的预测。
GM(1,1):灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程,进而用离散数据列建立微分方程形式的动态模型,由于这是本征灰色系统的基本模型,而且模型是近似的、非唯一的,故这种模型为灰色模型,记为 GM( Grey Model),即灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数, 建立起的微分方程形式的模型,这样便于对其变化过程进行研究和描述。
一次累加生成序列,均值生成序列,灰微分方程,白化微分方程,原理不明。
function []=greymodel(y)
% 本程序主要用来计算根据灰色理论建立的模型的预测值。
% 应用的数学模型是 GM(1,1)。
% 原始数据的处理方法是一次累加法。
y=input('请输入数据 ');
n=length(y);
yy=ones(n,1);
yy(1)=y(1);
for i=2:n
yy(i)=yy(i-1)+y(i);
end
B=ones(n-1,2);
for i=1:(n-1)
B(i,1)=-(yy(i)+yy(i+1))/2;
B(i,2)=1;
end
BT=B';
for j=1:n-1
YN(j)=y(j+1);
end
YN=YN';
A=inv(BT*B)*BT*YN;
a=A(1);
u=A(2);
t=u/a;
i=1:n+2;
yys(i+1)=(y(1)-t).*exp(-a.*i)+t;
yys(1)=y(1);
for j=n+2:-1:2
ys(j)=yys(j)-yys(j-1);
end
x=1:n;
xs=2:n+2;
yn=ys(2:n+2);
plot(x,y,'^r',xs,yn,'*-b');
det=0;
sum1=0;
sumpe=0;
for i=1:n
sumpe=sumpe+y(i);
end
pe=sumpe/n;
for i=1:n;
sum1=sum1+(y(i)-pe).^2;
end
s1=sqrt(sum1/n);
sumce=0;
for i=2:n
sumce=sumce+(y(i)-yn(i));
end
ce=sumce/(n-1);
sum2=0;
for i=2:n;
sum2=sum2+(y(i)-yn(i)-ce).^2;
end
s2=sqrt(sum2/(n-1));
c=(s2)/(s1);
disp(['后验差比值为:',num2str(c)]);
if c<0.35
disp('系统预测精度好')
else if c<0.5
disp('系统预测精度合格')
else if c<0.65
disp('系统预测精度勉强')
else
disp('系统预测精度不合格')
end
end
end
disp(['下个拟合值为 ',num2str(ys(n+1))]);
disp(['再下个拟合值为',num2str(ys(n+2))]);
回归放到下节回归分析。