- 【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
- 四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
- 语文主题教学学习笔记之87
东哥杂谈
“语文主题教学”学习笔记之八十七(0125)今天继续学习小学语文主题教学的实践样态。板块三:教学中体现“书艺”味道。作为四大名著之一的《水浒传》,堪称我国文学宝库之经典。对从《水浒传》中摘选的单元,教师就要了解其原生态,即评书体特点。这也要求教师要了解一些常用的评书行话术语,然后在教学时适时地加入一些,让学生体味其文本中原有的特色。学生也要尽可能地通过朗读的方式,而不单是分析讲解的方式进行学习。细
- 《转介绍方法论》学习笔记
小可乐的妈妈
一、高效转介绍的流程:价值观---执行----方案一)转介绍发生的背景:1、对象:谁向谁转介绍?全员营销,人人参与。①员工的激励政策、客户的转介绍诱因制作客户画像:a信任;支付能力;意愿度;便利度(根据家长具备四个特征的个数分为四类)B性格分类C职业分类D年龄性别②执行:套路,策略,方法,流程2、诱因:为什么要转介绍?认同信任;多方共赢;传递美好;零风险承诺打动人心,超越期待。选择做教育,就是选择
- JAVA学习笔记之23种设计模式学习
victorfreedom
Java技术设计模式androidjava常用设计模式
博主最近买了《设计模式》这本书来学习,无奈这本书是以C++语言为基础进行说明,整个学习流程下来效率不是很高,虽然有的设计模式通俗易懂,但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番,发现有大神写过了这方面的问题,于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类:创建型模式,共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式,共七种:适配器
- 新能源汽车 BMS 学习笔记篇—BMS 基本定义及分类
WPG大大通
其他笔记汽车BMS经验分享新能源电池
一、BMS定义1、概念:BMS(BatteryManagementSystem)即电池管理系统,其管理对象是二次电池(充电电池或蓄电池),其主要目的是电池的利用率,防止电池出现过度充电和过度放电,可应用于电动汽车、电瓶车、机器人、无人机等图片来源:腾讯网https://new.qq.com《标准普尔警告,电动汽车电池生产面临供应链和地缘政治风险》2、四大功能①感知和测量:检测电池的电压、电流、温度
- 吴恩达深度学习笔记(30)-正则化的解释
极客Array
正则化(Regularization)深度学习可能存在过拟合问题——高方差,有两个解决方法,一个是正则化,另一个是准备更多的数据,这是非常可靠的方法,但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高,但正则化通常有助于避免过拟合或减少你的网络误差。如果你怀疑神经网络过度拟合了数据,即存在高方差问题,那么最先想到的方法可能是正则化,另一个解决高方差的方法就是准备更多数据,这也是非常
- 个人学习笔记7-6:动手学深度学习pytorch版-李沐
浪子L
深度学习深度学习笔记计算机视觉python人工智能神经网络pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络(fullyconvolutionalnetwork,FCN)采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积(transposedconvolution)实现的,输出的类别预测与输入图像在像素级别上具有一一对应关系:通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
- golang学习笔记--MPG模型
xxzed
golang#学习笔记学习笔记golang
MPG模式:M(Machine):操作系统的主线程P(Processor):协程执行需要的资源(上下文context),可以看作一个局部的调度器,使go代码在一个线程上跑,他是实现从N:1到N:M映射的关键G(Goroutine):协程,有自己的栈。包含指令指针(instructionpointer)和其它信息(正在等待的channel等等),用于调度。一个P下面可以有多个G1、当前程序有三个M,
- 碎片化学习笔记分享
剑客写作
现在生活节奏很快,学习力成为了我们拥有的最大财富。碎片化学习是最好的。首先,不要太过自信,学会虚心学习,是我们面对现实的好方法,才能够常保新鲜。平时我们要拥有什么工具呢?1.思维导图2.写在印象笔记里3.听书,消燥耳机4.教学输出5.录音笔里面最好的方式就是教学输出法,记忆里最好。当输出时我们集中精力记忆里最好。有人认为缩短睡眠时间来学习,其实最好的方式是保持最好的睡眠,记忆力会更好。剥夺睡眠,会
- 《随园诗话》学习笔记三百零六
飞鸿雪舞
卷五凡诗之传者,都在灵性五、五斗米与诗【原文】丁丑,余觅一抄书人,或荐黄生,名之纪,号星岩者,人甚朴野。偶过其案头,得句云;“破庵僧卖临街瓦,独井人争向晚泉。”余大奇之,即饷米五斗。自此欣然大用力于诗。五言句云:“云开日脚直,雨落水纹圆。竹锐穿泥壁,蝇酣落酒尊。钓久知鱼性,樵多识树名。笔残芦并用,墨尽指同磨。"七言云:"小窗近水寒偏觉,古木遮天曙不知。旧生萍处泥犹绿,新落花时水亦香。旧甓恐闲都贮水
- D15 论语学习笔记
许小兔Angelina
悟:上级对下级的宽容:凡事成定局,就不你说了;已接近完结的事,也没必要匡正和挽回了;既然是过去的事,也没必要追究得失和责任了。对待孩子教育也是,不用“问责制”,这样容易让孩子因为害怕担责而说谎。应当循循善诱,避免再犯错才是最重要的。3.16:【原文】子曰:“射不主皮,为力不同科,古之道也。”【译文】孔子说:“射箭比赛不以射透为主,而主要看是否射得准确,因为人的力量不同,自古如此。”3.17:【原文
- 网络工程师学习笔记(一)
专业白嫖怪
网络工程师学习笔记学习笔记网络
为了备战下半年的软考——网络工程师,利用每天的下班的闲暇时间看书听课,然后自己手敲整理的系列资料。希望能够对你们有所帮助第一章__计算机网络概述计算机网络的定义:将分散的具有独立运算功能的计算机系统,通过通信线路和通信设备进行连接起来的实现资源的共享。ARPAnet网络的特征:资源共享、分散控制、分组交换1946年第一台通用计算机—埃尼亚克能够相互连通进行数据交换。1960年提出巨型网络,出现了对
- K8S学习笔记02——K8S组件
沉淅尘
#Docker#K8Skubernetes
Kubernetes组件一、控制平面组件(ControlPlaneComponents)(1)kube-apiserver(2)etcd(3)kube-scheduler(4)kube-controller-manager(5)cloud-controller-manager二、Node组件1.kubelet2.kube-proxy3.容器运行时(ContainerRuntime)三、插件(Add
- 「Python」2020.04.08学习笔记 | 第六章文件(a+)模式+把随机手机号写入文件小练习
Yetta的书影屋
学习测试开发的Day97,真棒!学习时间为40M第九次全天课(下午视频二20M-50M)>>>fp.seek(0)0>>>fp.read()'你好11你好12你好13你好14你好15\n你好16\n你好17\n你好18\n'>>>fp.seek(0,0)0>>>fp.write("*********************************\n")34>>>fp.seek(0,0)0>>>f
- 《金文成〈中庸〉学习笔记401。2020-2-24》
金吾生
《金文成〈中庸〉学习笔记401。2020-2-24》今天是庚子年戊寅月丁酉日,二月初二,2020年2月24日星期一。二月二龙抬头。第二十二章【唯天下至诚,为能尽其性;能尽其性,则能尽人之性;能尽人之性,则能尽物之性;能尽物之性,则能赞天地之化育;能赞天地之化育,则可以与天地参矣。】上一节,船山讲解说,性作为天用之本体,于圣人和匹夫匹妇而言并无二致,区别来自于诚。诚的区别来自于纯粹与掺杂。掺杂什么呢
- CDGA学习笔记三-《数据安全》
zy_chris
网络安全
七、数据安全7.1引言数据安全包括安全策略和过程的规划、建立与执行,为数据和信息资产提供正确的身份验证、授权、访问和审计。要求来自以下方面:(1)利益相关方(2)政府法规(3)特定业务关注点(4)合法访问需求(5)合同义务7.1.1业务驱动因素1、降低风险信息安全首先对组织数据进行分级分类,对组织数据进行分类分级的整个流程:1)识别敏感数据资产并分类分级2)在企业中查找敏感数据3)确定保护每项资产
- vue学习笔记——关于对Vue3 ref(), toRef(), toRefs(), unref(), isRef(), reactive()方法的理解。
chen_sir_sh
vue学习笔记javascript前端vue
VUE3出现了很多新的API,下面是自己的一些理解进行的总结。欢迎大家一起交流补充。ref()使用ref创建一个数据类型,ref有value这个属性constname1={age:"14",name:"bob1"};constname2=ref({name:"bob2"});//使用ref创建一个数据类型相对于reactive,ref有value属性name2.value="bob3"consol
- 遇到僵尸进程,怎么处理---学习笔记
summer@彤妈
性能优化linux
僵尸进程解释当iowait升高时,进程很可能因为得不到硬件的响应,而长时间处于不可中断状态。从ps或者top命令的输出中,你可以发现它们都处于D状态,也就是不可中断状态(UninterruptibleSleep)。既然说到了进程的状态,进程有哪些状态你还记得吗?我们先来回顾一下。top和ps是最常用的查看进程状态的工具,我们就从top的输出开始。下面是一个top命令输出的示例,S列(也就是Stat
- C++学习笔记----6、内存管理(五)---- 智能指针(3)
王俊山IT
c++学习笔记开发语言
2、shared_ptr有时候吧,有些对象或者一部分代码需要同一个指针的拷贝。那么unique_ptr不能被拷贝,因此就不能用于些场景。这样的话,std::shared_ptr就是一个支持能够被拷贝的拥有共享属主的智能指针。但是,如果有指向同一个资源的多个shared_ptr实例,那么怎么知道什么时候去释放资源呢?这可以通过对于引用记数来解决,这个我们以后再聊。首先,让我们看一下怎么构造与使用sh
- 【学习笔记】武志红心理学—潜意识决定命运
万万千千
冰山一角什么构成了我们的命运?命运是由我们的显意识和潜意识来决定的。我们可以用一张图做一个比喻。看过“冰山一角”图片的都知道,潜意识就是水面以下的部分,显意识是水面以上的部分,从体积来看,潜意识占了大部分,而显意识只是冰山一角,纵向来看,庞大的潜意识支撑着冰山一角的显意识,才得以让冰山漂浮在水面。延伸到我们的人生,我们对自己显意识层面的想法很容易感知到,所以我们会说这是“我”自己做的选择。而潜意识
- Prism 教程
yang_B621
PrismIOC
http://t.csdnimg.cn/VXSSvhttps://blog.csdn.net/u010476739/article/details/119341731Prism-随笔分类-Hello——寻梦者!-博客园(cnblogs.com)C#IoC学习笔记-缥缈的尘埃-博客园(cnblogs.com)WPF_SchuylerEX的博客-CSDN博客
- 绘本讲师训练营【第30期】2/21阅读原创《绘本之力》学习笔记2
郑贤钰
30028郑贤钰今天读了绘本之力《留在灵魂里的东西》读了心里有非常大的感触!两个年幼什么都不懂的孩子,为了自己心爱的东西,攒下来自己的零花钱,却买了一个自己不知道怎么用的东西,当他们觉得这个东西根本就不好,准备扔掉的时候,这是故事中的有趣有爱的老爷爷出现了,帮助孩子们再一次发现之前别人拉出优美的音乐,原来自己买的这一个琴,自认为没用的琴也能够经过老爷爷熟练的演奏也能拉出这样优美的声音,这让孩子们十
- 仿老师悟
耕海者
毕业十年了,今天去拜访老师,看到老师的学习笔记,看到老师努力学习,积极提高的状态,我觉着自己真是有些懈怠了,孩子们,老师的老师都在孜孜不倦,我们岂能偷懒!
- C++学习笔记----7、使用类与对象获得高性能(一)---- 书写类(2)
王俊山IT
c++学习笔记开发语言
2.2、定义成员函数前面对SpreadsheetCell类的定义足以让你生成类的对象。然而,如果想调用setValue()或者getValue()成员函数,连接器就会抱怨这些函数没有定义。这是因为到目前为止,这些成员函数只有原型,而还没有实现。通常,类的定义会在模块接口文件。对于成员函数的定义,你有一个选择:可以在模块定义文件或者在模块实现文件。下面是SpreadsheetCell类,在类内对成员
- Spring6学习笔记4:事务
·云扬·
SSMJava#Spring学习笔记spring
1JdbcTemplate1.1简介Spring框架对JDBC进行封装,使用JdbcTemplate方便实现对数据库操作准备工作①搭建子模块搭建子模块:spring-jdbc-tx②加入依赖org.springframeworkspring-jdbc6.0.2mysqlmysql-connector-java8.0.30com.alibabadruid1.2.15③创建jdbc.propertie
- 连通无向图一般中心的算法及其matlab程序详解
夏天天天天天天天#
图论算法matlab图论
#################本文为学习《图论算法及其MATLAB实现》的学习笔记#################若服务点只允许取在各顶点上,而服务对象却取在各顶点及各边(或弧)上的点,则在所有顶点中选定一个顶点作为图的一般中心其条件是该点离它本身的最远服务对象(包括顶点及各边(或弧)上的点)的距离达到极小值。寻找无向图的一般中心对解决网络最佳服务点确定的问题是十分有效的,使得服务对象的范围
- 学习笔记:FW内容安全概述
TKE_yinian
内容安全概述信息安全概述主要威胁关于防护简介内容安全威胁应用层威胁内容安全技术WEB安全应用安全入侵防御检测邮件安全数据安全网络安全反病毒全局环境感知沙箱检测信息安全概述•信息安全是对信息和信息系统进行保护,防止未授权的访问、使用、泄露、中断、修改、破坏并以此提供保密性、完整性和可用性。•为关键资产提供机密性、完整性和可用性(CIA三元组)保护是信息安全的核心目标。CIA(Confidential
- java的socket实现一个九宫棋游戏
睡不醒的小泽
前言一个简单的socket小作品=v=一个机酱在大三实验课中接触到很基础的JAVA语言socket编程。至于你问为什么嵌入式的机酱会弄些Java吗?emmmmm,可能是当初C语言版的不够好玩吧,另外如果碰巧有用,欢迎抱走的yoo在之前的笔记《网络基础知识和网络编程》中有讲解过关于网络编程的一些基本知识,以及一些LinuxC的socket编程,希望粗浅了解socket内部肌理的同学,右转咱的学习笔记
- 【每日一词】D33 edge
宠辱不惊的中年少女
1)学习笔记:edge:优势,=advantagebeanabsoluteedge有绝对优势AhasanedgeoverB表示A比B更好maintainone'sedge保持优势loseone'sedge失去优势innovativeedge创新方面的优势2)查字典延伸:A.就工作经验而言,她显然要比我们面试过的其他人都胜出一筹。Intermsofexperience,shedefinitelyha
- java工厂模式
3213213333332132
java抽象工厂
工厂模式有
1、工厂方法
2、抽象工厂方法。
下面我的实现是抽象工厂方法,
给所有具体的产品类定一个通用的接口。
package 工厂模式;
/**
* 航天飞行接口
*
* @Description
* @author FuJianyong
* 2015-7-14下午02:42:05
*/
public interface SpaceF
- nginx频率限制+python测试
ronin47
nginx 频率 python
部分内容参考:http://www.abc3210.com/2013/web_04/82.shtml
首先说一下遇到这个问题是因为网站被攻击,阿里云报警,想到要限制一下访问频率,而不是限制ip(限制ip的方案稍后给出)。nginx连接资源被吃空返回状态码是502,添加本方案限制后返回599,与正常状态码区别开。步骤如下:
- java线程和线程池的使用
dyy_gusi
ThreadPoolthreadRunnabletimer
java线程和线程池
一、创建多线程的方式
java多线程很常见,如何使用多线程,如何创建线程,java中有两种方式,第一种是让自己的类实现Runnable接口,第二种是让自己的类继承Thread类。其实Thread类自己也是实现了Runnable接口。具体使用实例如下:
1、通过实现Runnable接口方式 1 2
- Linux
171815164
linux
ubuntu kernel
http://kernel.ubuntu.com/~kernel-ppa/mainline/v4.1.2-unstable/
安卓sdk代理
mirrors.neusoft.edu.cn 80
输入法和jdk
sudo apt-get install fcitx
su
- Tomcat JDBC Connection Pool
g21121
Connection
Tomcat7 抛弃了以往的DBCP 采用了新的Tomcat Jdbc Pool 作为数据库连接组件,事实上DBCP已经被Hibernate 所抛弃,因为他存在很多问题,诸如:更新缓慢,bug较多,编译问题,代码复杂等等。
Tomcat Jdbc P
- 敲代码的一点想法
永夜-极光
java随笔感想
入门学习java编程已经半年了,一路敲代码下来,现在也才1w+行代码量,也就菜鸟水准吧,但是在整个学习过程中,我一直在想,为什么很多培训老师,网上的文章都是要我们背一些代码?比如学习Arraylist的时候,教师就让我们先参考源代码写一遍,然
- jvm指令集
程序员是怎么炼成的
jvm 指令集
转自:http://blog.csdn.net/hudashi/article/details/7062675#comments
将值推送至栈顶时 const ldc push load指令
const系列
该系列命令主要负责把简单的数值类型送到栈顶。(从常量池或者局部变量push到栈顶时均使用)
0x02 &nbs
- Oracle字符集的查看查询和Oracle字符集的设置修改
aijuans
oracle
本文主要讨论以下几个部分:如何查看查询oracle字符集、 修改设置字符集以及常见的oracle utf8字符集和oracle exp 字符集问题。
一、什么是Oracle字符集
Oracle字符集是一个字节数据的解释的符号集合,有大小之分,有相互的包容关系。ORACLE 支持国家语言的体系结构允许你使用本地化语言来存储,处理,检索数据。它使数据库工具,错误消息,排序次序,日期,时间,货
- png在Ie6下透明度处理方法
antonyup_2006
css浏览器FirebugIE
由于之前到深圳现场支撑上线,当时为了解决个控件下载,我机器上的IE8老报个错,不得以把ie8卸载掉,换个Ie6,问题解决了,今天出差回来,用ie6登入另一个正在开发的系统,遇到了Png图片的问题,当然升级到ie8(ie8自带的开发人员工具调试前端页面JS之类的还是比较方便的,和FireBug一样,呵呵),这个问题就解决了,但稍微做了下这个问题的处理。
我们知道PNG是图像文件存储格式,查询资
- 表查询常用命令高级查询方法(二)
百合不是茶
oracle分页查询分组查询联合查询
----------------------------------------------------分组查询 group by having --平均工资和最高工资 select avg(sal)平均工资,max(sal) from emp ; --每个部门的平均工资和最高工资
- uploadify3.1版本参数使用详解
bijian1013
JavaScriptuploadify3.1
使用:
绑定的界面元素<input id='gallery'type='file'/>$("#gallery").uploadify({设置参数,参数如下});
设置的属性:
id: jQuery(this).attr('id'),//绑定的input的ID
langFile: 'http://ww
- 精通Oracle10编程SQL(17)使用ORACLE系统包
bijian1013
oracle数据库plsql
/*
*使用ORACLE系统包
*/
--1.DBMS_OUTPUT
--ENABLE:用于激活过程PUT,PUT_LINE,NEW_LINE,GET_LINE和GET_LINES的调用
--语法:DBMS_OUTPUT.enable(buffer_size in integer default 20000);
--DISABLE:用于禁止对过程PUT,PUT_LINE,NEW
- 【JVM一】JVM垃圾回收日志
bit1129
垃圾回收
将JVM垃圾回收的日志记录下来,对于分析垃圾回收的运行状态,进而调整内存分配(年轻代,老年代,永久代的内存分配)等是很有意义的。JVM与垃圾回收日志相关的参数包括:
-XX:+PrintGC
-XX:+PrintGCDetails
-XX:+PrintGCTimeStamps
-XX:+PrintGCDateStamps
-Xloggc
-XX:+PrintGC
通
- Toast使用
白糖_
toast
Android中的Toast是一种简易的消息提示框,toast提示框不能被用户点击,toast会根据用户设置的显示时间后自动消失。
创建Toast
两个方法创建Toast
makeText(Context context, int resId, int duration)
参数:context是toast显示在
- angular.identity
boyitech
AngularJSAngularJS API
angular.identiy 描述: 返回它第一参数的函数. 此函数多用于函数是编程. 使用方法: angular.identity(value); 参数详解: Param Type Details value
*
to be returned. 返回值: 传入的value 实例代码:
<!DOCTYPE HTML>
- java-两整数相除,求循环节
bylijinnan
java
import java.util.ArrayList;
import java.util.List;
public class CircleDigitsInDivision {
/**
* 题目:求循环节,若整除则返回NULL,否则返回char*指向循环节。先写思路。函数原型:char*get_circle_digits(unsigned k,unsigned j)
- Java 日期 周 年
Chen.H
javaC++cC#
/**
* java日期操作(月末、周末等的日期操作)
*
* @author
*
*/
public class DateUtil {
/** */
/**
* 取得某天相加(减)後的那一天
*
* @param date
* @param num
*
- [高考与专业]欢迎广大高中毕业生加入自动控制与计算机应用专业
comsci
计算机
不知道现在的高校还设置这个宽口径专业没有,自动控制与计算机应用专业,我就是这个专业毕业的,这个专业的课程非常多,既要学习自动控制方面的课程,也要学习计算机专业的课程,对数学也要求比较高.....如果有这个专业,欢迎大家报考...毕业出来之后,就业的途径非常广.....
以后
- 分层查询(Hierarchical Queries)
daizj
oracle递归查询层次查询
Hierarchical Queries
If a table contains hierarchical data, then you can select rows in a hierarchical order using the hierarchical query clause:
hierarchical_query_clause::=
start with condi
- 数据迁移
daysinsun
数据迁移
最近公司在重构一个医疗系统,原来的系统是两个.Net系统,现需要重构到java中。数据库分别为SQL Server和Mysql,现需要将数据库统一为Hana数据库,发现了几个问题,但最后通过努力都解决了。
1、原本通过Hana的数据迁移工具把数据是可以迁移过去的,在MySQl里面的字段为TEXT类型的到Hana里面就存储不了了,最后不得不更改为clob。
2、在数据插入的时候有些字段特别长
- C语言学习二进制的表示示例
dcj3sjt126com
cbasic
进制的表示示例
# include <stdio.h>
int main(void)
{
int i = 0x32C;
printf("i = %d\n", i);
/*
printf的用法
%d表示以十进制输出
%x或%X表示以十六进制的输出
%o表示以八进制输出
*/
return 0;
}
- NsTimer 和 UITableViewCell 之间的控制
dcj3sjt126com
ios
情况是这样的:
一个UITableView, 每个Cell的内容是我自定义的 viewA viewA上面有很多的动画, 我需要添加NSTimer来做动画, 由于TableView的复用机制, 我添加的动画会不断开启, 没有停止, 动画会执行越来越多.
解决办法:
在配置cell的时候开始动画, 然后在cell结束显示的时候停止动画
查找cell结束显示的代理
- MySql中case when then 的使用
fanxiaolong
casewhenthenend
select "主键", "项目编号", "项目名称","项目创建时间", "项目状态","部门名称","创建人"
union
(select
pp.id as "主键",
pp.project_number as &
- Ehcache(01)——简介、基本操作
234390216
cacheehcache简介CacheManagercrud
Ehcache简介
目录
1 CacheManager
1.1 构造方法构建
1.2 静态方法构建
2 Cache
2.1&
- 最容易懂的javascript闭包学习入门
jackyrong
JavaScript
http://www.ruanyifeng.com/blog/2009/08/learning_javascript_closures.html
闭包(closure)是Javascript语言的一个难点,也是它的特色,很多高级应用都要依靠闭包实现。
下面就是我的学习笔记,对于Javascript初学者应该是很有用的。
一、变量的作用域
要理解闭包,首先必须理解Javascript特殊
- 提升网站转化率的四步优化方案
php教程分享
数据结构PHP数据挖掘Google活动
网站开发完成后,我们在进行网站优化最关键的问题就是如何提高整体的转化率,这也是营销策略里最最重要的方面之一,并且也是网站综合运营实例的结果。文中分享了四大优化策略:调查、研究、优化、评估,这四大策略可以很好地帮助用户设计出高效的优化方案。
PHP开发的网站优化一个网站最关键和棘手的是,如何提高整体的转化率,这是任何营销策略里最重要的方面之一,而提升网站转化率是网站综合运营实力的结果。今天,我就分
- web开发里什么是HTML5的WebSocket?
naruto1990
Webhtml5浏览器socket
当前火起来的HTML5语言里面,很多学者们都还没有完全了解这语言的效果情况,我最喜欢的Web开发技术就是正迅速变得流行的 WebSocket API。WebSocket 提供了一个受欢迎的技术,以替代我们过去几年一直在用的Ajax技术。这个新的API提供了一个方法,从客户端使用简单的语法有效地推动消息到服务器。让我们看一看6个HTML5教程介绍里 的 WebSocket API:它可用于客户端、服
- Socket初步编程——简单实现群聊
Everyday都不同
socket网络编程初步认识
初次接触到socket网络编程,也参考了网络上众前辈的文章。尝试自己也写了一下,记录下过程吧:
服务端:(接收客户端消息并把它们打印出来)
public class SocketServer {
private List<Socket> socketList = new ArrayList<Socket>();
public s
- 面试:Hashtable与HashMap的区别(结合线程)
toknowme
昨天去了某钱公司面试,面试过程中被问道
Hashtable与HashMap的区别?当时就是回答了一点,Hashtable是线程安全的,HashMap是线程不安全的,说白了,就是Hashtable是的同步的,HashMap不是同步的,需要额外的处理一下。
今天就动手写了一个例子,直接看代码吧
package com.learn.lesson001;
import java
- MVC设计模式的总结
xp9802
设计模式mvc框架IOC
随着Web应用的商业逻辑包含逐渐复杂的公式分析计算、决策支持等,使客户机越
来越不堪重负,因此将系统的商业分离出来。单独形成一部分,这样三层结构产生了。
其中‘层’是逻辑上的划分。
三层体系结构是将整个系统划分为如图2.1所示的结构[3]
(1)表现层(Presentation layer):包含表示代码、用户交互GUI、数据验证。
该层用于向客户端用户提供GUI交互,它允许用户
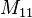 represents the total number of attributes where
A and
B both have a value of 1.
represents the total number of attributes where
A and
B both have a value of 1.
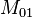 represents the total number of attributes where the attribute of
A is 0 and the attribute of
B is 1.
represents the total number of attributes where the attribute of
A is 0 and the attribute of
B is 1.
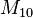 represents the total number of attributes where the attribute of
A is 1 and the attribute of
B is 0.
represents the total number of attributes where the attribute of
A is 1 and the attribute of
B is 0.
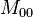 represents the total number of attributes where
A and
B both have a value of 0.
represents the total number of attributes where
A and
B both have a value of 0.
