DBSCAN聚类算法

1、算法引入及简介

     为什么要引入DBSCAN？

     K均值聚类使用非常广泛，作为古老的聚类方法，它的算法非常简单，而且速度很快。但是其缺点在于它不能识别非球形的簇；而DBSCAN算法是将所有点标记为核心点、边界点或噪声点，将任意两个距离不大于E（eps）的核心点归为同一个簇，任何与核心点足够近的边界点也放到与之相同的簇中，可以发现任意形状的簇类。

   人为构造基于sin函数和cos函数构成的两组点数据，分别用K均值与DBSCAN算法聚类，对比如下：

         

                                      K均值                                                                                                         DBSCAN

      可以发现K均值聚类结果是不理想的

       

        DBSCAN定义

      

      DBSCAN(Density-Based Spatial Clustering of Application with Noise)，是一个较有代表性的基于密度的聚类算法。它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。简单的说就是过滤低密度区域，把扎堆的点（高密度区域）找出来。

2、相关概念
   

    1）密度：任意一点的密度是以该点为圆心、以E为半径的圆区域内包含的点数目。   4
    2）Ε邻域：给定对象半径为Ε内的区域称为该对象的Ε邻域。
    3）核心对象：如果对象的E邻域样本点数大于等于MinPts（最小样本点数）,则称该对象为核心对象。   a
    4）边界点：在以半径为E的邻域内点的数量小于MinPts,但是落在其他核心点的邻域内。    d
    5）噪声点：既不是边界点也不是核心点的任意点。   e
           

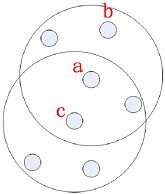
   6）直接密度可达：对于样本集合D，如果样本点q在p的Ε领域内，并且p为核心对象，那么对象q从对象p直接密度可达（如果p是一个核心对象，q属于p的邻域，q从p直接密度可达）。

                       a为核心对象，b为边界对象，b从a直接密度可达,反过来不成立,因为b不是核心对象

     7）密度可达：对于样本集合D，给定一串样本点p1,p2….pn，p= p1,q= pn,假如对象pi从pi-1直接密度可达，那么对象q从对象p密度可达。

               b从a直接密度可达，a从c直接密度可达, 故b从c密度可达，同理c从b密度不可达

     

      8）密度相连：存在样本集合D中的一点o，如果对象o到对象p和对象q都是密度可达的，那么p和q密度相连。
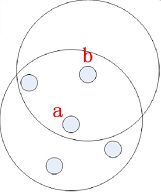
            b从a密度可达,c也从a密度可达，故b和c密度相连。

示例

    

       

     如图，E用相应半径表示，设MinPts=3
     m、p、o、r为核心对象，s、q为边界点（对应E领域内点的个数为2      q和p从m直接密度可达，m从p直接密度可达，故p从q密度可达,p和q密度相连
     s和r从o密度可达，s和r密度相连

3、算法描述

    

    输入: 包含n个对象的数据库，半径E，最小样本点MinPts;
    输出:所有生成的簇。
  (1)Repeat
  (2)从数据库中抽出一个未处理的点;
  (3)IF抽出的点是核心点 THEN 找出所有从该点密度可达的对象，形成一个簇;
  (4)ELSE 抽出的点是边缘点(非核心对象)，跳出本次循环，寻找下一个点；
  (5)UNTIL 所有的点都被处理。

 3.1步骤

 

  （1）DBSCAN需要二个参数: 扫描半径 (E)和最小包含样本点数(MinPts)。 任选一个未被访问(unvisited)的点开始，找出与其距离在E之内(包括E)的所有附近点。

  （2）如果 附近点的数量 ≥ minPts，则当前点与其附近点形成一个簇，并且出发点被标记为已访问(visited)。 然后递归，以相同的方法处理该簇内所有未被标记为已访问(visited)的点，从而对簇进行扩展。

  （3）如果 附近点的数量 < minPts，则该点暂时被标记作为噪声点。

  （4）如果簇充分地被扩展，即簇内的所有点被标记为已访问，然后用同样的算法去处理未被访问的点。

  3.2具体实现过程
  

   (1)检测数据库中尚未检查过的对象p，找出与其距离在E之内(包括E)的所有附近点，若包含的对象数不小于MinPts，建立新簇C，将其中的所有点加入候选集N;

   (2)对候选集N 中所有尚未被处理的对象q，检查其邻域，若至少包含minPts个对象，则将这些对象加入N;如果q 未归入任何一个簇，则将q 加入C;

   (3)重复步骤2)，继续检查N 中未处理的对象，当前候选集N为空;

   (4)重复步骤1)~3)，直到所有对象都归入了某个簇或标记为噪声。

  3.3实例
   

    如下二维数据集，设E=3.MinPts=3,使用DBSCAN对其聚类

   

     先扫描样本点P1（1，2）

          计算其E邻域，即找样本点中与其距离不大于E的样本点
          P1样本点的E邻域为：{P1、P2、P3、P13}
          P1的密度为4>MinPts,因此P1是核心点

          以P1点建立新簇C1，令N为P1邻域内的点的集合
          对N中的每一个点q，如果q未处理过且是核心点，则将q邻域内的点并入N。如果q还不是任何簇的成员，把q添加到C1
                 对P2邻域为{P1，P2，P3，P13}，为核心点且未处理过将其邻域内的点并入N，把P2添加到C1
                 对P3，邻域为{P1，P2，P3，P4，P13}，同上，将P3邻域内的点并入N，把P3添加到C1
                 对P13，邻域为{P1，P2，P3，P4，P13}，同上，将P13邻域内的点并入N，把P13添加到C1
                 继续考虑N中未处理的点P4，邻域为{P3，P4，P13}，将P4邻域内的点并入N, 把P4添加到C1
       此时集合N中对象全部处理完毕，得到簇C1，包含点{P1，P2，P3，P4，P13}
       继续扫描样本点P5（5，8），同上得簇C2，包含{P5，P6，P7，P8}
       继续扫描样本点P9（9，5）：
            计算其E邻域为{P9}，为非核心点
       继续扫描样本点P10（1，12）：
            P10样本点的E邻域为{P10，P11}，为非核心点
       继续扫描样本点P11（3，12）：
            P11 样本点E邻域为{P10，P11,P12},P11是核心点
            以P11点建立新簇C3，令N为P11邻域内点的集合
            对N中的每一个点q，如果q未处理过且是核心点，则将q邻域内的点并入N。如果q还不是任何簇的成员，把q添加到C1

                  对P10，非核心点，把P10加入C3
                  对P12，邻域为{P11,P12}，非核心点，把P12加入C3
     此时N中对象处理完毕得到簇C3

     继续扫描样本点，P12和P13都已经处理过，算法结束

     最后聚类结果为：3个簇    C1{P1,P2,P3,P4,P13}    C2{P5,P6,P7,P8}    C3{P10,P11,P12}

     样本点P9未归类为任何一个，最后判定为噪声

  3.4算法伪代码

 

       其中ExpandCluster算法伪码如下：

 

    

   3.5关于E和MinPts参数的选择

  

      给定MinPts

      1)E值过大：很多噪声被错误的归入簇，分离的若干个               自然簇错误的合并为一个簇

      2)E值过小：大量对象被错误的标记为噪声

      给定E值

      1)MinPts值过大：核心点数量减少，使得一些包含对象数较少的自然簇被弄丢

      2)MinPts值过小：大量对象被标记为核心点，从而将噪声归入簇

4、算法优缺点及改进

    

    4.1优点：

      １）与K-means方法相比，DBSCAN不需要事先知道要形成的簇类的数量。
      ２）与K-means方法相比，DBSCAN可以发现任意形状的簇类。
      ３）同时，DBSCAN能够识别出噪声点。
      ４）DBSCAN对于数据库中样本的顺序不敏感，但是，对于处于簇类之间边界样本，可能会根据哪个簇类优先被探测到而其归属有所摆动。

   

    4.2缺点：
      １）于高维数据，密度定义较麻烦。
      ２）簇的密度变化太大，会有麻烦。

   4.3算法改进

   

     一种基于距离的自适应确定参数E和MinPts的方法

    

     (1)给定数据集P={p(i); i=0,1,…n}，对于任意点P(i)，计算点P(i)到集合D的子集S={p(1), p(2), …, p(i-1), p(i+1), …, p(n)}中所有点之间的距离，距离按照从小到大的顺序排序，假设排序后的距离集合为D={d(1), d(2), …, d(k-1), d(k), d(k+1), …,d(n)}，则d(k)就被称为k-距离。也就是说，k-距离是点p(i)到所有点（除了p(i)点）之间距离第k近的距离。对待聚类集合中每个点p(i)都计算k-距离，最后得到所有点的k-距离集合E={e(1), e(2), …, e(n)}

    

     (2)对集合E进行升序排序后，绘出曲线，通过观察，将急剧发生变化的位置所对应的k-距离的值，确定为半径Eps的值

    

     (3)在上述E确定的情况下，统计数据集中每个点的E邻域内点的数目，然后对整个数据集中每个点的E邻域内的点的数目求数学期望得到MinPts,此时的MinPts为每个聚类中核心对象E邻域内的数据点个数的最优值。计算公式为:

       
                                                                 

         其中，Pi为点i的的E邻域内点的个数