生成函数
生成函数
生成函数是组合计数中的一个重要工具,总结一下吧~
定义
在数学中,某个序列 an 的母函数(又称生成函数)是一种形式幂级数,其每一项的系数可以提供关于这个序列的信息。使用母函数解决问题的方法称为母函数方法。
母函数可分为很多种,包括普通母函数、指数母函数、L级数、贝尔级数和狄利克雷级数。对每个序列都可以写出以上每个类型的一个母函数。构造母函数的目的一般是为了解决某个特定的问题,因此选用何种母函数视乎序列本身的特性和问题的类型。
类型
普通母函数
普通母函数就是最常见的母函数,一般来说,序列 (an) 的母函数是: ∑∞n=0an∗xn。
设 ak,bk,ck 是已知的序列,它们的普通型生成函数分别为 A(x),B(x),C(x) 。
(本段摘抄至离散数学教材。。)
1) 若 bk=αak ,α为常数,则 B(x)=αA(x) 称为 A(x) 的常数倍。
2) 若 ck=ak+bk ,则 C(x)=A(x)+B(x) 称为 A(x) 与 B(x) 的和。
3) 若 ck=∑ki=0aibk−i ,则 C(x)=A(x)B(x) 称为 A(x) 与 B(x) 的积。
(3)的形式就是两个多项式的相乘,使用FFT我们就可以 O(nlogn) 得出c序列。
应用
普通母函数常用于多重集组合问题。
考虑如下的经典问题:对于非负整数 x1,x2,x3,...xk,求x1+x2+x3+..+xk=n 有多少组非负整数解。
我们可以为每个变量构造一个生成函数,这里每个的权值都是1,所以每个变量得到的生成函数均为 1+x+x2+...+xn+...+ (不选为1,选i个为 xi ,这里变量的取值没有限制,所以生成函数有无穷多项),变量的组合相加对应于生成函数的乘积,这样我们将这些多项式相乘得到 f(x)=(1+x+x2+...+xn+..)k ,将 f(x) 展开,则其中 xn 这一项的系数即为此方程解的个数。
这里给出一个常见的化简公式:
1+x+x2+...+xn+...=11−x 。
上式之所以成立,是因为我们假设 −1<x<1 ,而不关注具体x的取值,这是没有意义的。
由上式可以很容易得出接下来的式子:
∑∞i=0xki=11−xk 。
11−ax=1+ax+a2x2+a3x3+....+anxn+...+.. .
还有一个这样的式子: 11+x−x2=1(1+5√+12x)(1+1−5√2x) ,这里化成多项式后 xn 这一项的系数为 ∑ni=0(5√+12)i∗(1−5√2)n−i.
继续上面的问题,这样我们得到了 f(x)=(1−x)−k ,使用广义二项式定理展开得到
这里可以看出 xn 项的系数为 (n+k−1k−1) ,这与我们用插板法得到的结论是相同的。
上述例子给出了使用普通母函数来解决组合问题的一个常见思路,为每个数构造一个生成函数,组合得到n的方案数即为 xn 这一项的系数。
如果没办法像上面的例子一样通过公式化简怎么办?那么我们可以考虑使用背包dp来计数。
整数划分问题
说到普通母函数,不得不提另外一个经典的问题:整数划分问题。
问题如下:使用正整数相加组合成n的方案有多少种。
比如4有以下几种:1+1+1+1, 2+2,4,1+3,1+1+2。
初看这个问题不是很简单嘛: dp[i][j] 表示使用不大于j的正整数来组成i的方案数,那么 dp[i][j]=dp[i−j][j]+dp[i][j−1] ,如果 j>i ,那么 dp[i][j]=dp[i][i] 。
如果需要求1到n(n<=1e5)内每个数呢?
dp复杂度太高,无法承受。这里就要用到五边形数定理了~。
五边形数:组成刚好n个五边形的点的数量称为五边形数,第n个五边形数为 3n2−n2 ,那么五边形数序列为1,5,12,22,35,51…..
广义五边形数组成的序列是当上式中n取0,1,-1,2,-2,…x,-x…时得到的数值,即0,1,2,5,7,12,15….
我们定义将n拆分为一些正整数的和的方案数为p(n)。
有如下结论:
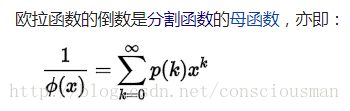

欧拉函数 φ(x) 的展开为
这里我们不必要去知道这个怎么证明得来的,只需要知道分割函数的生成函数以及五边形数定理即可~。
有了五边形数定理,我们就可以 O(nn√) 求出1到n内每个数的分割数了。
如下,具体参见 hdu 4651。
#include 指数型母函数
序列 (an) 的指数型母函数是: ∑∞n=0an∗xnn!。
序列 an 的指数型生成函数与 bn 的指数型生成函数相乘,得到的新序列的系数 ck=∑ki=0(ki)aibk−i ,只要使用FFT,我们同样可以得出两个指数型生成函数多项式的乘积。
应用
指数型母函数适用于解决多重集排列问题。
这里给出指数型生成函数常见的化简公式:
∑∞i=0xii!=ex ;
1−x1!+x22!−...+(−1)nxnn+..=e−x 。
所以只取偶数项的指数型生成函数为 ex+e−x2 ,只取奇数项的指数型生成函数为 ex−e−x2 。
①数列 rn 的指数型生成函数为 erx=∑∞i=0(rx)ii! 。
②数列{0,1,0,-1,0,1,0,-1….}的指数型生成函数为sin(x)。
③数列{1,0,-1,0,1,0,-1,0….}的指数型生成函数为cos(x)。
④设 A=a1,a2,a3….an 是n元集,从中可重复地选取r个元作排列,那么作成的排列数 er 是 E(t)=∏ni=1∑xtt! 展开式中 xrr! 的系数,式中t是 ai 这个元可以选取的次数。
有了上述定理,我们就可以解决一些复杂的多重集排列问题了~
考虑如下的一个简单问题:
把n个彼此相异的球放到4个不同的盒子 A1,A2,A3,A4 中,求使得A_1 A1 中含有奇数个球,A_2 A2 含有偶数个球的不同的放球方法数g_n gn 。
解:任意一种方案对应于A_1,A_2,A_3,A_4 A1,A2,A3,A4 的一个多重集排列.
A1 的生成函数为
A2 的生成函数为
A3和A4 均为
所以
所以 gn=4n−1 。
除上述两种外,还存在其他类型的生成函数,但是在此就不多介绍了。
(没出现过题目而且我不会-_-)
下面来看一些题目吧~
习题
先来看个水题压压惊。。。
hdu 2082 找单词
传送门
题意:给出26个字母的个数,字母c的价值为c-‘A’+1,求求能够组成的总价值小于50的单词个数(单词只与选的字母有关,与排列顺序无关)。
分析:非常水的普通母函数,这里每个字母个数有限制,我们暴力dp算系数就可以。
#include poj 3734 Blocks
传送门
题意:N块砖排成一行,每块砖可以被涂成红、蓝、绿、黄四种颜色,求最后涂为红、绿的砖的数目均为偶数的方案数。
分析:很水的指数型生成函数。可以知道 E(t)=e2t∗(ex+e−x2)2 ,化简得到第n项的系数即为 4n+2n+14 。
当然这题还可以矩阵快速幂。
#include poj 1322
传送门
题意:包裹里有无限个分布均匀且刚好c种颜色的巧克力,现在要依次拿n个出来放到桌子上,每次如果桌子上面有两种相同颜色的巧克力就会把这两个巧克力给吃掉,求最后桌子上面还有m个巧克力的概率。
分析:概率dp是可行的,令dp[i][j]表示拿i个巧克力出来后桌子上面还剩j个巧克力的概率。这样复杂度就是 O(NC) 的,无法承受,但是注意到题目只要求输出三位小数,通过打表找规律可以发现在n大于一定数值的时候,后面的值都是与奇偶有关了,做1000次迭代就已经远超过精度要求了。
本题当然可以直接生成函数搞:
还剩m个巧克力,也就是说有m种颜色选了奇数次,有c-m种颜色选了偶数次。
取n个巧克力出来刚好就对应于c种颜色的一个多重集排列。总共可能有 cn 个排列,现在我们只需要算出有多少种可能的排列满足上述要求即可。
生成函数相乘得到 E(t)=(ex+e−x2)c−m∗(ex−e−x2)m. 如果分子当中 xnn! 这一项的系数为a,那么答案即为 (cm)a2c∗cn 。
这里分子为
这是两个多项式的积,数据范围很小,我们直接暴力算就可以。左右两个多项式相乘后会得到 (−1)m−j(c−mi)(mj)ex(2i+2j−c) 的形式,我们只需要暴力枚举i,j,然后算其对答案的贡献: (−1)m−j(c−mi)(mj)(2i+2j−cc)n。
不过本人不是很明白,为什么一定要用快速幂计算 (2i+2j−cc)n 。用对数搞就是各种wa,1e-3的精度开long double也还是wa。。。
#include codeforces 451E Devu and Flowers
传送门
题意:有n(n<=20)种花,每种花的数量 fi(<=1e12) 已知,现在要取 si(si<=1e14) 朵,求方案数。
分析:数据范围明显没办法dp,但是注意到n很小。带有限制的计数问题我们都可以考虑容斥原理。
所以我们只需要这样算即可:没有任何限制的方案数-一种限制不满足的方案数+两种限制不满足的方案数-….
没有任何限制的方案数在最开始已经讨论过了,就是n个变量和为s的非负整数解的个数。有一些限制不满足的话,那么就说明某种花用的数量大于 fi 了,这样的话我们只需要令 s−=fi+1 ,将解的下界重新变为0就可以转化了相同的问题了。复杂度 O(2n)。
#include hdu 4658 Integer Partition
传送门
题意:求n的整数划分方案,其中没有任意一个整数出现超过k-1次。
分析:结论题。。如果是n的整数划分方案,那么可以直接用五边形数定理 O(nn√) 预处理。
不过这里同样是有结论的,定义定义将n拆分为一些正整数的和且任意一种正整数的个数不能大于等于m的方案数为pp(n)。
pp(n) = p(n) – p(n-m) – p(n-2m) + p(n-5m)+p(n-7m)-….这里也是广义五边数序列。
#include hdu 6042 Journey with Knapsack
传送门
题意:一个体积为 2∗n 的背包,有 n(n<=5e4) 种食物,第i种食物的体积是i,数量是 ai(0<=a1<a2<...<an<=2n) ,还有m种装备,第i种装备的体积是 bi(1<=bi<=2∗n) ,求装一些食物和一件装备使得背包装满的方案数。
分析:很明显的组合问题,我们首先考虑装食物的方案数。
首先为每一种食物构造生成函数然后相乘得到 f(z)=∏ni=1(1+xi+x2i+...+xaii)=∏ni=11−xi(ai+1)1−xi。
我们尝试把上述式子分解然后合并:
之所以需要将式子分解是因为我们从最初的f(z)无法直接算系数,如果暴力dp算系数复杂度太高无法承受。
因为我们只需要计算1到2n的系数,所以多项式合并时是在 mod x2n+1 意义下进行的。
看第一个积式 ∏2ni=111−xi ,这个就是1到2n内每个数的整数划分方案p(n)的生成函数!
那么我们就可以将式子变为:
那么我们将第一个多项式与第二积式的每一项的那个多项式合并。
p(i)xi 与 1−xj(aj+1) 合并得到 p(i)xi−p(i)xi+j(aj+1) 。
这样我们只需要从大到小更新 xi(j∗(aj+1)<=i<=2n) 的系数即可,可以知道 (aj+1)∗j>=j2 ,只有 O(n√) 项会更新第一个和式的系数,总复杂度 O(nn√) 。
然后我们考虑与最后一项 ∏2nk=n+11−xk 的合并。
在 mod x2n+1 意义下, ∏2nk=n+11−xk=1−∑2nk=n+1xk 。
那么现在我们合并得到
这样我们枚举装的装备,得到 ans=∑mi=1p′′(2n−bi) 。
#include bzoj 3771 Triple
传送门
题意:给n个互不相同的数 ai ,现在可以任选一个、两个或者三个数,需要输出这些数所有可能的和sum,以及每个sum下组成sum的方案数。
分析:选一个数直接加上即可;
选两个数,那么这就是一个明显的FFT了,对权值为0或者1的序列做自卷积即可,需要减去一个数选两次的情况,然后除2即可。
选三个数,就是同样地序列做两次卷积。减掉一个数选超过一次的情况,然后除以6即可。
构造三个01序列,分别为 a[i],b[i∗2],c[i∗3] ,简单地容斥一下,那么选两个数的情况就是 (a[i]∗a[i]−b[i])/2 ,选三个数的情况就是 (a[i]∗a[i]∗a[i]−3∗a[i]∗b[i]+2∗c[i])/6 。
我们只需要在DFT意义下直接算,然后将结果IDFT回来就行了。
#include
//i做正常的+1,j左反转类型的+1,始终保持i和j是反转的
k = len / 2;
while (j >= k) j -= k, k /= 2;
if (j < k) j += k;
}
}
//做FFT,len必须为2^k形式,on==1时是DFT,on==-1时是IDFT
void fft(Complex y[], int len, int on) {
change(y, len);
for (int h = 2; h <= len; h <<= 1) {
Complex wn(cos(-on * 2 * PI / h), sin(-on * 2 * PI / h));
for (int j = 0; j < len; j += h) {
Complex w(1, 0);
for (int k = j; k < j + h / 2; k++) {
Complex u = y[k];
Complex t = w * y[k + h / 2];
y[k] = u + t;
y[k + h / 2] = u - t;
w = w * wn;
}
}
}
if (on == -1) for (int i = 0; i < len; i++) y[i].x /= len;
}
const int N = 150003;
Complex a[N], b[N], c[N], d[N];
int main() {
int n, m = 0, va;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &va);
a[va] = b[va << 1] = c[va*3] = Complex(1, 0);
}
m = va * 3;
int l = 1;
while (l <= m) l <<= 1;
fft(a, l, 1); fft(b, l, 1); fft(c, l, 1);
for (int i = 0; i <= l; i++) {
d[i] = d[i] + a[i];
d[i] = d[i] + (a[i] * a[i] - b[i]) * Complex(0.5, 0);
d[i] = d[i] + (a[i] * a[i] * a[i] - Complex(3, 0) * a[i] * b[i] + Complex(2, 0) * c[i]) * Complex(1.0 / 6, 0);
}
fft(d, l, -1);
for (int i = 0; i <= l; i++) {
int ans = (int)(d[i].x + 0.5);
if (ans) printf("%d %d\n", i, ans);
}
return 0;
} bzoj 3028 食物
传送门
题意:明明出去旅游,他带的食物和它们的限制如下:
承德汉堡:偶数个
可乐:0个或1个
鸡腿:0个,1个或2个
蜜桃多:奇数个
鸡块:4的倍数个
包子:0个,1个,2个或3个
土豆片炒肉:不超过一个。
面包:3的倍数个
求带N个食物的方案数。
分析:明显的生成函数,我们考虑为每一种食物建立生成函数然后相乘。
这里我们可以知道 1(1−x)4 关于第n项的系数是 (n+33) ,乘上x之后那么答案就是 (n+23) 。
import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
static Scanner in = new Scanner(System.in);
public static void main(String[] args) {
BigInteger s = in.nextBigInteger(), t = s.add(BigInteger.ONE);
BigInteger L = s.multiply(t).multiply(t.add(BigInteger.ONE));
L = L.divide(BigInteger.valueOf(6));
System.out.println(L.mod(BigInteger.valueOf(10007)));
}
}bzoj 4772 显而易见的数论
传送门
题意:给定整数 n(n<=2000) ,和一个长为 k(k<=1e5) 的序列 ai(ai<=1e7) ,求n的每一种划分方案的价值之和,假设n的一种划分方案的所有整数组成的序列为p,长为m,那么n的这一种划分方案的价值为 ∑mi=1∑mj=i+1g(aF(p[i],p[j])%k) 。这里 g(n)=∑ni=1(i−1,n)∗[(i,n)==1] 。
输入时会给定一个整数type,当 type=1,F(x,y)=1 ,当 type=2 时, F(x,y)=gcd(x,y) ,当 type=3 时, F(x,y)=xy+yx+x xor y 。
分析:看完题目有一种绕地球几圈的感觉。。。不过这个题还是值得一做的。。
这里枚举每一个划分方案显然是不现实的,我们可以计算每一对 pi,pj 的贡献。这样我们就可以知道每一个 ai 出现的次数了,那么最终 ans=∑k−1i=0cnt[i]∗g(a[i]) 。cnt[i]表示 ai 出现的次数。
那么问题就转化为每两个小于n的整数x,y在所有划分方案中出现的次数了。
如果x!=y,且x和y在一个划分方案数出现了a次和b次,那么x和y贡献的次数就是a*b次,我们可以换个角度,也就是说a和b出现的次数中每一对数(c,d)1<=c<=a,1<=d<=b)在这个划分方案都要被统计一次,两者刚好是等价的,这样我们直接枚举每一对数 x,y 和其出现的次数 c,d ,假设 F(x,y)%k==s ,那么 cnt[s]+=∑x∗c<=n∑x∗c+y∗d<=np(n−x∗c−y∗d) 。 p(n) 表示n的划分方案的个数。
如果 x==y 呢?那么我们是不能这么计算的,因为两者并不等价,如果一个划分方案中x出现了 d 次,那么(x,x)贡献的次数就是 d∗(d−1)2 。我们计算出刚好只有 d个x 的划分方案的个数,这个个数很容易计算-> p(n−x∗d)−p(n−x∗(d+1)) 。
所以问题变得清晰了,预处理p(n),gcd(x,y)、x^y以及g函数,然后计算cnt[i]即可。
现在我们来考虑g函数的性质。
gcd是积性函数,那么g函数也是积性函数。
g(x)=g(a)g(b) ,其中 (a,b)==1 。
对于函数g(x),对于多素因子的合数,我们不好在线性筛时计算,所以我们可以考虑将x转化为两个互质的数的函数之积,也就是如果 x=∏ti=1peii ,那么 g(x)=g(pe11)∗g(∏ti=2peii) 。
对于 pe 这样形式的数, g(pe) 就变得很容易计算了。
这里 (pi−1,pe)==1 ,通过反证法很容易证明得出。所以后面那一项只有 pe−1 个数与 pe 不互质。
那么我们有 g(pe)=∑ei=0pi∗φ(pe−i)−pe−1=(e+1)(pe−pe−1) 。
在线性筛的时候记录每一个数的最小的质因数的幂 pe11 ,假设为q[i]。然后对于质数p,g(p)=2*p-2。
令T = s * p,那么
另外, g(n)=d(n)∗φ(n) ;我们可以通过线性筛 d(n) 与 φ(n) 得出 g(n) 。
到了这里问题已经解决了~
ps:这里s%p==0&&q[s]==s这一种情况容易忽略。。。本题还是出的挺好的。
#include hdu 6067 Big Integer
传送门
题意:Q 喜欢 k(k<=10) 进制下的大整数,这个整数不能包含0,且每个数字c出现的次数不能超过 n(n<=14000) 次。他有一个 (k−1)∗(n+1) 的矩阵 g , gi,j 为0代表这个他喜欢的大整数中i这个数字不能刚好出现j次。每天他的口味会变化,也就是矩阵中的某一个位置会翻转。总共有 m(m<=200) 天,求 ∑mi=0cnt[i] mod 786433。 cnt[i] 表示第i天后Q喜欢的整数的个数。
分析:首先我们可以计算出初始时Q喜欢的整数个数,这个可以通过生成函数求出,每个数i的生成函数为 f(i)=∑nj=0gijxjj! 。
那么我们只需要求 ∏k−1t=1f(i) 的系数即可。k比较小,这里我们可以直接NTT。
初始的答案我们可以直接先算出来;考虑变化,对于一个翻转u、v。它只会影响到第f(u)这个多项式DFT的过程。 Xk=∑N−1n=0an(gp−1N)nk 。这里p是模数,N是序列长度,g是原根。一次操作只会加上或者删除 1v! 这一项,那么对于f(u) DFT的过程会使得 X0,X1,...XN−1 加上或者减去 1v!,1v!(gp−1N)v,1v!(gp−1N)2v...1v!(gp−1N)(N−1)v 。这是一个等比数列。
令 V[i]=∏ti=1Xi(0<=i<N) ,这样一次修改操作我们可以直接 O(N) 的完成,在V[i]中除去这一项(乘上逆元)、修改 Xv ,然后在给V[i]乘上去即可。为了方便计算,我们考虑记录每一项中0的个数。
总时间复杂度 O(nk2log(nk)+mnk) 。做完这题,可以回顾一下FFT的原理了~
#include CodeForces - 438E The Child and Binary Tree
传送门
题意:给定长为 n(n<=1e5) 的 c 序列,以及 m(m<=1e5) ,构造二叉树,每个点的权值必须是 c 序列中的数,而一颗二叉树的总权值为树中所有节点的权值之和,输出m个数,第i个数代表总权值为i的二叉树的个数。
分析:做了就长姿势了。。
首先,我们可以很容易地得出递推式,令 fi 表示总权值为 i 的二叉树的个数,那么 fi=∑w∈{c1,c2,...cn}∑i−wj=0fj∗fi−w−j 。
很容易看出来后面的和式是个卷积。这里我们通过生成函数来化简求解。
令 F(x) 是 f 的生成函数, g(x)=∑xi=0fi∗fx−i ,那么 fi=∑w∈{c1,c2,...cn}gi−w ,实际上这里还是个卷积的形式。
我们知道,如果 f(x)=∑ni=0aixi,g(x)=∑ni=0bixi ,那么两个生成函数的乘积 f(x)g(x) 中每一项 xn 的系数是 ∑ni=0aibn−i 。
那么如果 c 序列的生成函数为 C(x) ,这里就有 F(x)=C(x)∗F2(x)+1 。后面的 +1 是 f0 。
所以我们可以得到 F(x)=21+1−4C(x)√ 。
那么现在到了问题的关键了,如何求F(x),我们只需要做一次多项式开根和一次多项式求逆,就可以得出f的生成函数,进而得到f序列了。
在这里就可以学会多项式求逆和多项式开根,2333。。
还可以看看picks大牛的博客。
这算是第一次做自己感觉高级的内容了。。哈哈,感觉挺有意思的。。
#include