hdu 1542 upcoj 2540 矩形面积并 线段树
几天没AC了 。。。太爷跟我说什么有个线段树的题很简单,可以做一下。。于是被坑了。。
那个题是upcoj 2540,求一堆矩形重叠2次部分的面积,现在我还只会线段树简单的点修改区间修改,呵呵呵一看这题我果断不会做。。百度了一下,看了太爷给的一个不错的线段树汇总http://www.notonlysuccess.com/index.php/segment-tree-complete/,算是对这种矩形面积并的类型有点了解了,最基础的是hdu 1542,求矩形面积的和,upcoj上重叠2次的是这种问题的变形。
这种题目的方法是扫描线法。先把所有x坐标记录,排序,把一个矩形的上下两条线加入结构体,按y坐标排序。注意一般的线段树区间[L,R]就是指[L,R],这里区间[L,R]指的是[x[L],x[R]]这段区间,L是点x[L],R是点x[R],取mid的时候也是x[mid]。所谓扫描线就是假设有一根线顺着y坐标从下往上扫。
hdu 1542
Atlantis
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 6082 Accepted Submission(s): 2661
The input file is terminated by a line containing a single 0. Don’t process it.
Output a blank line after each test case.
有两种方法,第一种方法比较慢,感觉也没有第二种方法好理解,看看就行了。这种方法对于每个y坐标的扫描线的区间就是这条线的[x1,x2],并且update的时候必须要找到线段树底。
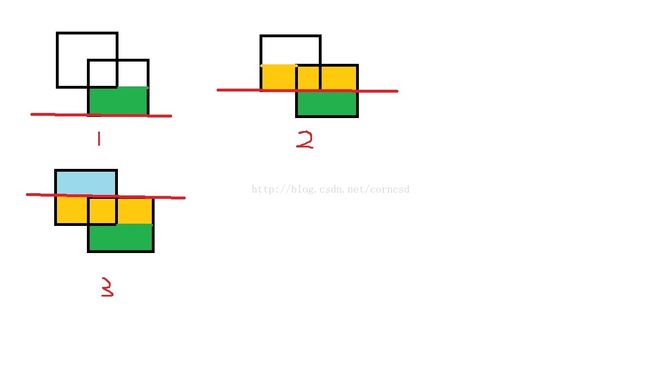
红色代表扫描线,update的时候ly[o]代表[L,R]这个区间上一次扫描线的y坐标,l[o]和r[o]代表x[L]和x[R],covered[o]代表这个区间目前有几条线覆盖(如果covered不为0,说明当前位置在矩形内部),初始化的时候把下面的边cover设为1,上面的边cover设为-1。这种方法几乎是需要查询到叶子节点的,而且感觉没有通用性。
#include
#include
#include
#include
#include
#include
#include 推荐第二种方法,更好理解,并且可以用于这个问题的变形,更新的时候不用查找到叶子节点,效率明显高。
这里的扫描线当作无限长,最上面的边不用扫,设sum[o]为节点o区间共有多长的距离被覆盖,那么扫描每条线的时候用sum[1]乘以下一条线的高度减去这条线的高度(因为这部分肯定是在矩形中的),covered[o]是区间o有多少条完全覆盖这个区间的线,扫描每个线的时候更新区间的covered,维护sum。
注意我用的区间代表的是点,比如L,就代表排序后x[L]这个点,这样的话更新的时候区间分别是[L,mid],[mid,R]而不是mid+1了,这样的话树的高度可能会比以前多一层。如果用L代表排序后x[L]到x[L+1]这条线段,就还是以前的[L,mid],[mid+1,R]了。
update之前用了二分找当前线的左右坐标分别是第几个点,其实也可以不用找,像第一种方法那样在更新的时候判断也可以。
#include
#include
#include
#include
#include
#define INF 0x3f3f3f3f
#define MAXN 210
#define MAXNODE 4*MAXN
#define pi 4*atan(1)
using namespace std;
int N,M,covered[MAXNODE];
double sum[MAXNODE],x[MAXN];
struct Line{
double x1,x2,y;
int cover;
bool operator < (const Line & a) const{
return yv) R=mid;
else L=mid+1;
}
return -1;
}
void maintain(int o,int L,int R){
if(covered[o]) sum[o]=x[R]-x[L];
else if(L+1>=R) sum[o]=0;
else sum[o]=sum[o<<1]+sum[o<<1|1];
}
void update(int o,int L,int R,int l,int r,int cover){
if(l<=L&&r>=R){
covered[o]+=cover;
maintain(o,L,R);
return;
}
int mid=(L+R)>>1;
if(lmid) update(o<<1|1,mid,R,l,r,cover);
maintain(o,L,R);
}
int main(){
//freopen("in.txt","r",stdin);
int cas=0;
while(scanf("%d",&N),N){
int NX=1;
M=0;
double x1,y1,x2,y2;
for(int i=0;i upc 2540
2540: Monitoring System
Time Limit: 5 Sec Memory Limit: 128 MBSubmit: 39 Solved: 11
[ Submit][ Status][ Web Board]
Description
BCBC is a large bank. To ensure safety, they have set many cameras to monitor the total bank. Recently, they have found some problems in the monitoring system. In the current system, a camera can monitor a rectangle region. Some regions can be monitored by three or more cameras, which is waste; some regions can only be monitored by just one camera, which is not safe. So the manage intends to improve the system. Now he wants to know how many regions are monitored by just two cameras..
Input
There are multiple test cases. Each test case begins with an integer n (1<=n<=100000) standing for the number of cameras. Then n lines follow. Each line has four integers x1, y1, x2, y2 (1
Output
. Each test case output one integer that is the area of regions covered by just exactly two cameras, the result occupied one line.
Sample Input
Sample Output
求覆盖2次的面积和。只要求出覆盖2次以上和3次以上的面积和相减就行。代码和上面的几乎相同,就是维护sum的时候要维护sum1,sum2,sum3,分别代表覆盖1次、2次、3次的面积和。维护sum2和sum3的函数和sum1有点不同。
#include
#include
#include
#include
#include
#define INF 0x3f3f3f3f
#define MAXN 200010
#define MAXNODE 4*MAXN
#define pi 4*atan(1)
using namespace std;
int N,M,covered[MAXNODE],sum1[MAXNODE],sum2[MAXNODE],sum3[MAXNODE],x[MAXN];
struct Line{
int x1,x2,y,cover;
bool operator < (const Line & a) const{
return yv) R=mid;
else L=mid+1;
}
return -1;
}
void maintain1(int o,int L,int R){
if(covered[o]) sum1[o]=x[R]-x[L];
else if(L+1>=R) sum1[o]=0;
else sum1[o]=sum1[o<<1]+sum1[o<<1|1];
}
void maintain2(int o,int L,int R){
if(covered[o]>=2) sum2[o]=x[R]-x[L];
else if(covered[o]==1){
if(L+1>=R) sum2[o]=0;
else sum2[o]=sum1[o<<1]+sum1[o<<1|1];
}
else{
if(L+1>=R) sum2[o]=0;
else sum2[o]=sum2[o<<1]+sum2[o<<1|1];
}
}
void maintain3(int o,int L,int R){
if(covered[o]>=3) sum3[o]=x[R]-x[L];
else if(covered[o]==2){
if(L+1>=R) sum3[o]=0;
else sum3[o]=sum1[o<<1]+sum1[o<<1|1];
}
else if(covered[o]==1){
if(L+1>=R) sum3[o]=0;
else sum3[o]=sum2[o<<1]+sum2[o<<1|1];
}
else{
if(L+1>=R) sum3[o]=0;
else sum3[o]=sum3[o<<1]+sum3[o<<1|1];
}
}
void update(int o,int L,int R,int l,int r,int cover){
if(l<=L&&r>=R){
covered[o]+=cover;
maintain1(o,L,R);
maintain2(o,L,R);
maintain3(o,L,R);
return;
}
int mid=((L+R)>>1);
if(lmid) update(o<<1|1,mid,R,l,r,cover);
maintain1(o,L,R);
maintain2(o,L,R);
maintain3(o,L,R);
}
int main(){
freopen("in.txt","r",stdin);
int cas=0;
while(scanf("%d",&N)!=EOF){
int NX=1,x1,y1,x2,y2;
M=0;
for(int i=0;i