图
图的定义
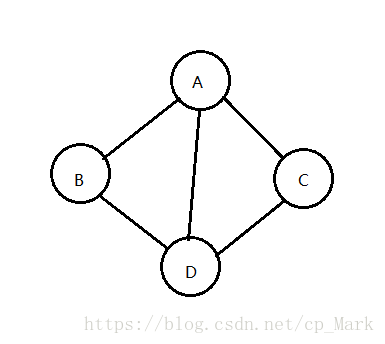
定义:图(Graph)是由顶点的有穷非空集合和顶点之间的集合组成,通常表示为:G(V、E),其中G表示一个图,V是图G中顶点的集合,E是图G中边的集合。下图就是一个图的示例:

在图的定义过程中,有几点我们需要注意的:
(1)在图中数据元素,我们称之为顶点
(2)在图结构中,不允许没有顶点
(3)图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的
各种图的定义
无向图
若顶点vi到vj之间没有方向,则称这条边为无向边,用无序偶对(vi,vj)来表示。如果图中任意两个顶点之间的边都是无向边,则称该图为无向图。示意图如下:
有向图
若从顶点vi到vj的边有方向,则称这条边为有向边,也称为弧。用有序偶对
在有向图中有一点需要注意的:因为有向边是有方向的,所以有序偶顺序不能调换,比如上图中的
简单图
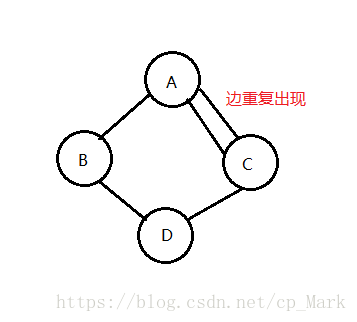
在图中,若不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。我们讨论的图都是简单图,如下两个就不是简单图:
无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2条边。示意图如下:

有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边。示意图如下:

稠密图、稀疏图
有很少条边或弧的图称为稀疏图,反之称为稠密图。这里的稀疏和稠密概念是相对而言的,根据实际情况来定义。
网
有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫作权。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网。示意图如下:

子图
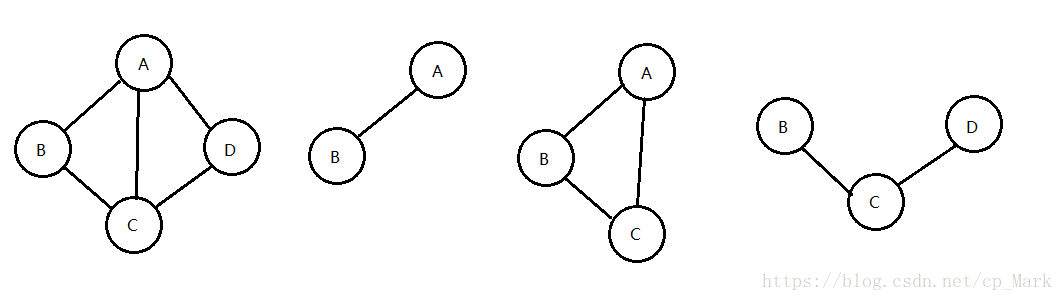
假设有两个图G和 G ’ G{’} G’,如果 V ′ V{'} V′属于V且 E ′ E{'} E′属于E,则称 G ′ G{'} G′为G的子图。示意图如下(左侧第一个为原图,右侧几个为子图):
图的顶点与边间的关系
无向图
对于无向图G=(V,{E}),如果边(v, v ′ v{'} v′)∈ E,则称顶点v和 v ′ v{'} v′互为邻接点,即v和 v ′ v{'} v′相邻接。边(v, v ′ v{'} v′)依附于顶点v和 v ′ v{'} v′,或者说(v, v ′ v{'} v′)与顶点v和 v ′ v{'} v′相关联。顶点v的度是和v相关联的边的数目,即为TD(v)。
无向图G=(V,{E})中从顶点v到顶点 v ′ v{'} v′的路径是一个顶点序列。
有向图
对于有向图G=(V,{E}),如果弧
有向图G=(V,{E})中从顶点v到顶点 v ′ v{'} v′的路径是一个顶点序列(有向的)。
补充
路径的长度是路径上的边或弧的数目。
第一个顶点到最后一个顶点相同的路径称为回路或环。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路或简单环。示意图如下:

连通图相关术语
无向图
在无向图G中,如果从顶点v到顶点 v ′ v{'} v′有路径,则称v和 v ′ v{'} v′是连通的。如果对于图中任意两个顶点vi、vj∈V,vi和vj都是连通的,则称G为连通图。示意图如下:
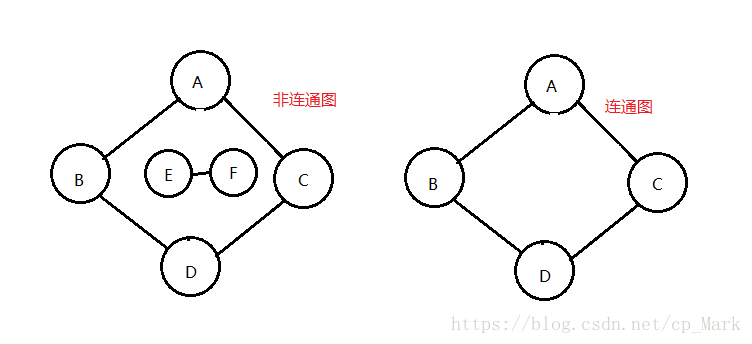
无向图中的极大连通子图称为连通分量。连通分量有几点需要强调:
(1)要是子图
(2)子图要是连通的
(3)连通子图含有极大顶点数
(4)具有极大顶点数的连通子图包含依附于这些顶点的所有边
有向图
在有向图G中,如果对于每一对vi、vj∈V,vi≠vj,从vi到vj和从vj到vi都存在路径,则称G为强连通图。有向图中的极大强连通子图称作有向图的强连通分量。示意图如下:

补充
生成树:一个连通图的生成树是一个极小的连通子图,它含有图中全部的n个顶点,但只有足以构成一棵树的n-1条边。示意图如下(右侧两图为左侧的生成树):

注意:n-1条边并不一定是生成树
有向树:如果一个有向图恰有一个顶点的入度为0,其余顶点的入度均为1,则是一棵有向树。
有向图的生成森林:一个有向图的生成森林由若干棵有向树组成,含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧。示意图如下:

图的抽象数据类型
ADT图(Graph)
Data
顶点的有穷非空集合和边的集合
Operation
CreateGraph(*G,V,VR):按照顶点集V和边弧集VR的定义构造图
DestroyGraph(*G):图G存在则销毁
LocateVex(G,u):若图G中存在顶点u,则返回其在图中的位置
GetVex(G,v):返回G中顶点v的值
PutVex(G,v,value):将图G中顶点v赋值value
FirstAdjVex(G,*v):返回顶点v的一个邻接顶点,若顶点在G中无邻接顶点返回空
NextAdjVex(G,v,*w):返回顶点v相对于顶点w的下一个邻接顶点,若w是v的最后一个顶点则返回“空”
InsertVex(*G,v):在图G中增添新顶点v
DeleteVex(*G,v):删除图G中顶点v及其相关的弧
InsertArc(*G,v,w):在图G中增添弧,若G是无向图,还需要增添对称弧
DeleteArc(*G,v,w):在图G中删除弧,若G是无向图,则还删除对称弧
DFSTraverse(G):对图G中进行深度优先遍历,在遍历过程对每个顶点调用
HFSTraverse(G):对图G中进行广度优先遍历,在遍历过程对每个顶点调用
endADT
图的存储结构
邻接矩阵
考虑到图是由顶点和边或弧两部分组成。合在一起比较困难,我们很自然地把它分到两个结构中来存储。顶点不分大小、主次,所以用一个一位数组来存储;而边或弧由于是顶点与顶点之间的关系,一维搞不定,我们使用二维数组来存储。
定义:图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
下面是分别针对几种图的邻接矩阵示例:
(1)无向图

从上面我们可以发现,邻接矩阵包含两个组成元素:顶点数组、边数组,因为这是简单图,所以对角线全为0(没有到达自身顶点的边),从图中可以看出v0和v1连通,所以它们之间的值为1,以此类推。
从上图中我们可以得到以下内容:
1)很容易判定任意两个顶点是否有边
2)很容易求得某个顶点的度(直接看一行或一列有几个为1)
3)很容易知道某个顶点的邻接点
(2)有向图
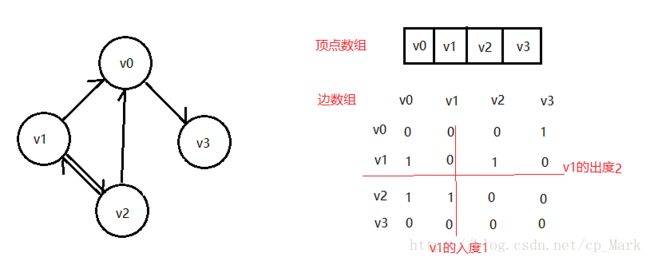
基本上与无向图是一致的,唯一不同的地方就在于,有向图顶点的度是由出度(弧尾)和入度(弧头)组合而成,行为出度,列为入度。
(3)网图
设图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:

这里的w值表示(vi,vj)或

顶点结构
//顶点类型由用户定义
typedef char VertexType;
//边上的权值类型由用户定义
typedef int EdgeType;
//最大顶点数,由用户定义
#define MAXVEX 100;
//用65535代表不可能的数
#define INFINIFY 65535;
typedef struct{
//顶点表
VertexType vex[MAXVEX];
//邻接矩阵,可看作边表
EdgeType arc[MAXVEX][MAXVEX];
//图中当前的顶点数和边树
int numVertexes,numEdges;
}MGraph;
邻接表
邻接矩阵是一个不错的图存储结构,但是对于边数相对顶点较少的图,这种结构就会造成很大的空间浪费。所以出现了数组+链表的组合方式来存储图信息,我们把这种数组+链表向结合的存储方法称为邻接表。
邻接表的处理办法是这样的:
(1)图中的顶点还是用一个一维数组来存储
(2)图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表来实现。
无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表
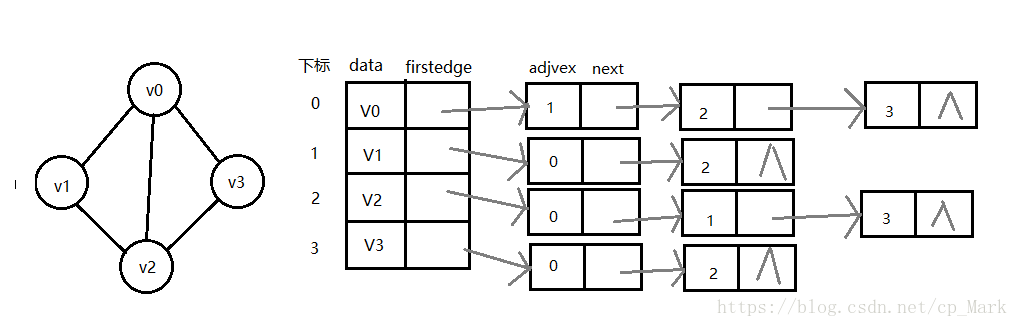
顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。
边表结点由adjvex和next两个域组成,adjvex是邻接点域,存储某顶点的邻接点在顶点表的下标,next则存储指向边表中下一个结点的指针。如上图中,和v0相邻接的有v1、v2、v3,即顶点表对应坐标右侧的整个链表中的所有结点都是和v0邻接的。以此类推。
(2)有向图

我们发现有向图的邻接表中多了一个逆邻接表,因为有向图是有向的,我们默认是以顶点为弧尾来存储边表的,但是当我们需要确定顶点的入度时就比较麻烦了,所以有了逆邻接表,即以顶点为弧头的邻接表。其字段含义和无向图中一致就不再赘述了。
(3)网
网图的邻接表实际上和有向图的邻接表是差不多的,唯一的区别就是多了一个weight数据域(权重)。

顶点结构
//顶点类型由用户定义
typedef char VertexType;
//边上的权值类型由用户定义
typedef int EdgeType;
//最大顶点数,由用户定义
#define MAXVEX 100;
//用65535代表不可能的数
#define INFINIFY 65535;
//边表结点
typedef struct EdgeNode{
//邻接点域,存储该顶点对应的下标
int adjvex;
//用于存储权值,对于非网图可以不需要
EdgeType weight;
//链域,指向下一个邻接点
struct EdgeNode *next;
}EdgeNode;
//顶点表结点
typedef struct VertextNode{
//顶点域,存储顶点信息
VertexType data;
//边表头指针
EdgeNode *firstedge;
}VertextNode,AdjList[MAXVEX];
typedef struct{
//顶点表
AdjList adjList;
//图中当前的顶点数和边树
int numVertexes,numEdges;
}GraphAdjList;