作者:Jacob Bandes-Storch,原文链接,原文日期:2015/08/05
译者:Lou;校对:shanks;定稿:shanks
这篇博文启发自Code Review.SE上的一个讨论,同时nerd-sniped上的关于数学的有趣的学习。让我对数学和 Swift 的结合有了兴趣。所以我花了一段时间来把这些知识整理成一篇博文,特别是自从我完成了对我网站重建的第一步以后。更重要的是,我希望我能更勤勉的更新我的博客,这8年我只写了一篇而已,希望大家能对我的博客感兴趣。
这篇博文的目标对于初学者来讲,比较容易理解,同时也提供给那些已经对这个概念熟悉的人一些有用的细节和例子。希望大家能给我反馈。
假设你第一次学习 Swift,你实在是太兴奋了,花了一天时间反复练习,等到第二天就成了专家。于是第二天你就开始传授课程来教别人。
当然,我很愿意成为你的第一个学生。我也学的很快,一天学下来,我也可以教别人 Swift 了。我俩继续教别人,其他的学生也学的很快,马上跟上进度,都可以第二天就去教别人。
这是个多么让人兴奋的世界呀。但是问题来了,照这样的进度下去,Swift 学习者将大量涌入城市,基础设施将无法支撑庞大的人口。
市长叫来最好的科学家们:“我们需要精确的数学模型!每天到底有多少人会使用 Swift?什么时候这种疯狂会终止?”
搭建数学模型
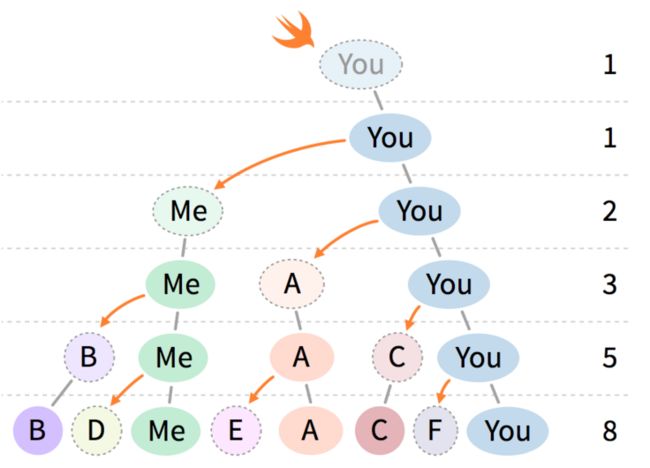
仔细观察我们发现,特定的一天总的 Swifters 数量(我们用 \\(S_{今天}\\) 来表示)等于前一天的数量加上每个老师可以所教的学生。
$$ S_{今天} = S_{昨天} + 老师数 $$
那么老师数目是多少呢?记住,一个人需要花一天时间学习才能变成 Swift 专家,所以前天的每一个人都能成为老师,都可以教一个学生:\\(S_{今天} = S_{昨天} + S_{前天}\\)。
这下公式就简单了!我们可以用手算了:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
...如果这个数列看上去有点熟悉,那是因为这是斐波纳契数列。
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,...
不管你是否喜欢,我们的世界里处处都有斐波那契数的存在:花瓣的生长遵循斐波那契数列,大树的枝丫是斐波那契树丫,当然也有人吐槽说这不过是确认偏误罢了。我们发现,这个数列是基于非常简单的形式的,非常容易计算:
var i = 0
var j = 1
while true {
(i, j) = (j, i + j)
print(i) // 打印1, 然后打印1, 继续打印2, 3, 5, 8, 13, 21, 34, 55...
}
大功告成!
哈哈,骗你的。我们才刚刚开始。计算机美妙的地方就在于可以帮助我们快速的解决用手算很麻烦的问题。让我们尝试几个例子。
42天后有多少个 Swifter?
前面我们已经差不多解决了这个问题,只要在42那边停止循环即可。
var i = 0
var j = 1
for _ in 0..<42 {
(i, j) = (j, i + j)
}
i // returns 267914296
那么第 n 天呢?
和之前的问题类似,我们可以将其抽象成一个函数。用 n 来代替 42。
func nthFibonacci(n: Int) -> Int
{
var i = 0
var j = 1
for _ in 0..第一周到底写了多少 Swift?
为了简化问题,假定每个人写代码的速度是一样的。知道每个人每天写的代码量后,我们只需要把斐波那契数加起来即可。
func fibonacciSumUpTo(n: Int) -> Int
{
var sum = 0
for i in 0..逐步简化
不要急,Swift 的标准库里面已经有了一个函数叫做 reduce,可以将数字加在一起。我们该怎么写呢?
[1, 1, 2, 3, 5, 8, 13].reduce(0, combine: +) // 返回 33这样可行,但是我们需要把每个数字都写出来。要是能用 nthFibonacci() 就好了。
既然这些是连续的斐波那契数,我们可以简单的使用1到7的范围:
[1, 2, 3, 4, 5, 6, 7].map(nthFibonacci)
// 返回 [1, 1, 2, 3, 5, 8, 13]
[1, 2, 3, 4, 5, 6, 7].map(nthFibonacci).reduce(0, combine: +)
// 返回 33或者我们可以更简单,用 Swift 的range operator(...):
(1...7).map(nthFibonacci).reduce(0, combine: +) // 返回 33这等同于 fibonacciSumUpTo
性能优化
看上去很不错,但是不要忘了 nthFibonacci(i) 从0开始加到 i,所需的工作量将随着i线性增加。
而且我们所写的 (1...n).map(nthFibonacci).reduce(0, combine: +) 从1到n每次凑要运行 nthFibonacci, 这将大大增加运算量。
注意:计算越简单的斐波那契数,真实耗费每一步的时间几乎可以忽略不计(开启性能优化)。这篇文章之前的草稿版本包括了时间消耗的表格,但是我把表格去掉了,怕误导大家。取而代之的是,我们讨论的是一个相对的时间/性能的复杂度。
让我们将 nthFibonacci 和 fibonacciSumUpTo 两个函数结合来减少一点运算量:
func fastFibonacciSumUpTo(n: Int) -> Int
{
var sum = 0
var i = 0
var j = 1
for _ in 0..现在我们已经将 fastFibonacciSumUpTo 的复杂度从二次降为线性了。
但是为了实现这个,我们不得不写了一个更加复杂的方程。我们在分离相关度(把计算斐波那契数和求和分为2步) 和优化性能之间进行了权衡。
我们的计划是用 Swift 的标准库来简化和解开我们的代码。首先我们来总结一些我们要做什么。
将前n个斐波那契数用线性时间(linear time)和常量空间(constant space)的方式加起来。
将前n个斐波那契数用线性时间(linear time)和常量空间(constant space)的方式加起来。
将前n个斐波那契数用线性时间(linear time)和常量空间(constant space)的方式加起来。
幸运的是,Swift 正好有我们需要的功能!
1、 reduce 函数,用 + 操作符来结合。
2、 prefix 函数和惰性求值(Lazy Evaluation)
注意:prefix只有在 Xcode 7 beta 4中可用,作为 CollectionTypes 的一个全局函数使用,但其实已经在 OS X 10.11 beta 5 API 作为 SequenceType 的扩展出现了。我期望在下一个 Xcode beta 有一个延迟实现的版本;现在这里有一个自定义的实现。
3、 定制数列,使用数列型协议(SequenceType protocol)
定制数列
Swift 的 for-in 循环的基础是 SequenceType 协议。所有遵循这个协议的可以循环。
想要成为一个 SequenceType 只有一个要求,就是提供一个创建器( Generator ):
protocol SequenceType {
typealias Generator: GeneratorType
func generate() -> Generator
}而成为一个 GeneratorType 只有一个要求,就是生产元素( Elements )
protocol GeneratorType {
typealias Element
mutating func next() -> Element?
}所以一个数列就是一个可以提供元素创建器的东西。
最快创建定制数列的方法就是用AnySequence。这是一个内建的结构体,可以响应generate(),去调用一个你在初始化时所给的闭包。
struct AnySequence: SequenceType {
init
(_ makeUnderlyingGenerator: () -> G)
} 类似的,我们可以用 AnyGenerator 和 anyGenerator 函数来造创建器。
func anyGenerator(body: () -> Element?) ->
AnyGenerator 所以写一个斐波那契数列就相当简单了:
let fibonacciNumbers = AnySequence { () -> AnyGenerator in
// 为了创建一个生成器,我们首先需要建立一些状态...
var i = 0
var j = 1
return anyGenerator {
// ... 然后生成器进行改变
// 调用 next() 一次获取每一项
// (代码看起来是不是很熟悉?)
(i, j) = (j, i + j)
return i
}
}
现在 fibonacciNumbers 是一个 SequenceType,我们可以使用 for 循环:
for f in fibonacciNumbers {
print(f) // 打印 1, 然后打印 1, 继续打印 2, 3, 5, 8, 13, 21, 34, 55...
}而且我们可以自由的使用 prefix:
for f in fibonacciNumbers.prefix(7) {
print(f) // 打印 1, 1, 2, 3, 5, 8, 13, 然后停止.
}最后我们可以用 reduce 来加起来:
fibonacciNumbers.prefix(7).reduce(0, combine: +) // 返回 33太棒了!这是线性时间的,常量空间的,最重要的是这非常清晰的展示了我们所要做的,而不需要使用 ... 和 map。
说明:如果你在playground里运行这段代码,可能会发现这个版本比之前的要慢。这个版本只改变了常数部分,复杂度本身没有变化,但是性能却有明显下降。和 fastFibonacciSumUpTo 进行对比可以发现,这段代码把单一的循环改成了函数调用,这可能就是性能降低的原因。没错,我们又需要进行权衡。
灵活度
目前的目标只是给了我们一个更好给工具去解答有关斐波那契数的问题。深入钻研来看,我们可能会问:为什么我要先研究斐波那契数?这不过是这个数列恰好符合我们所发现的规律:
$$S_{今天} = S_{昨天} + S_{前天}$$
这个公式在我们代码中表现为 (i, j) = (j, i + j)。但是这深藏了 AnySequence 和 anyGenerator。如果我们要写更加清晰的代码 --- 可以描述我们想要解决的问题、不需要仔细分析 --- 我们最好写的更加明显点。
斐波那契数列常写成这种形式:
$$F_{n} = F_{n-1} + F_{n-2}$$
这是类似的形式,但是最重要的是这表现出递推关系。这种数学关系指的是数列里某一个数的值取决于前面几个数的值。
定义递推关系的时候,首先要定义初始项。我们不能简单的利用 (i, j) = (j, i + j) 来计算斐波那契数如果我们不知道什么是 i 什么是 j。在我们的例子里,我们的初始项为 i = 0 和 j = 1 —— 或者,我们可以把初始值定为1和1,因为我们是等第一个值返回以后才进行计算的。
递推关系的阶数(order)是指每一步所需的前面项的个数,而且初始项数目必须等于阶数(不然的话我们就没有足够的信息来计算下一项)。
现在我们可以来设计API了!你只需提供初始项和递推就可以创建递推关系了:
struct RecurrenceRelation
{
/// - Parameter initialTerms: The first terms of the sequence.
/// The `count` of this array is
/// the **order** of the recurrence.
/// - Parameter recurrence:
Produces the `n`th term from the previous terms.
/// - 参数 initialTerms: 序列的第一个元素集合.
/// 数组的个数也就代表这个递推的排序。
/// - 参数 recurrence:根据前面的元素推算出第 n 个元素
init(_ initialTerms: [Element], _ recurrence:
(T: UnsafePointer, n: Int) -> Element)
} (我们在使用 UnsafePointer 而不是 [Element],这样我们就可以使用 T[n] 而不需要存储先前计算的项)。
现在,我们的初始任务变得更加简单了。多少人在使用Swift? 只要用这个公式即可:
let peopleWritingSwift = RecurrenceRelation([1, 1])
{ T, n in T[n-1] + T[n-2] }
peopleWritingSwift.prefix(7).reduce(0, combine: +) // 返回 33
那么,如何来实现这个API呢?
我们来做吧。
struct RecurrenceRelation: SequenceType, GeneratorType
{ 首先我们需要一些内存来存储元素,还需要一个引用来链接到我们所要传递的闭包。
private let recurrence: (T: UnsafePointer, n: Int) -> Element
private var storage: [Element]
/// - 参数 initialTerms: 序列的第一个元素集合.
/// 数组的个数也就代表这个递推的排序。
/// - 参数 recurrence:根据前面的元素推算出第 n 个元素
init(_ initialTerms: [Element], _ recurrence: (T: UnsafePointer, n: Int) -> Element)
{
self.recurrence = recurrence
storage = initialTerms
} 为了简单点,我们同时采用 SequenceType and GeneratorType。对于 generate(),我们只返回 self。
// SequenceType requirement
func generate() -> RecurrenceRelation { return self } 接下来,每次调用 next(),我们调用 recurrence 来产生下一个值, 并且将其存在 storage 里。
// GeneratorType requirement
private var iteration = 0
mutating func next() -> Element?
{
// 首先推算出所有的初始元素值
if iteration < storage.count { return storage[iteration++] }
let newValue = storage.withUnsafeBufferPointer { buf in
// 调用闭包,传入内存地址中的指针的偏移量,知道 T[n-1] 是数组中最后一个元素
return recurrence(T: buf.baseAddress +
storage.count - iteration, n: iteration)
}
// 存储下一个的值,丢弃到最旧的值
storage.removeAtIndex(0)
storage.append(newValue)
iteration++
return newValue
}
}
更新:@oisdk指出
UnsafePointer不是必须的。在原来的版本中,我使用它是为了让 n 的值在 recurrence 中更加精确 - 但是自从 recurrence 只依赖与前一项,而不是 n 本身时,n 的值不再改变时,这是ok的。 所以这个版本运行良好。不使用UnsafePointer感觉更加安全了!
记住:有许多种方法可以定义自定义数列。CollectionType,SequenceType,和 GeneratorType 只是协议,你可以按照自己所需的方式来遵循它们。也就是说,在实践中也许你很少需要这么做 —— Swift 的标准库里有大多数你所需的。不过如果你觉得需要自定义的数据结构,你可以使用 CollectionType 和 SequenceType。
更多的例子
现在我们已经归纳了递推关系,我们可以轻松地计算许多东西了。比如说卢卡斯数(Lucas Number)。和斐波那契数类似,只不过初始项不同:
// 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521...
let lucasNumbers = RecurrenceRelation([2, 1]) { T, n in T[n-1] + T[n-2] }或者”Tribonacci Numbers“,一个拥有有趣性质的三阶递推:
// 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504...
let tribonacciNumbers = RecurrenceRelation([1, 1, 2])
{ T, n in
T[n-1] + T[n-2] + T[n-3]
}
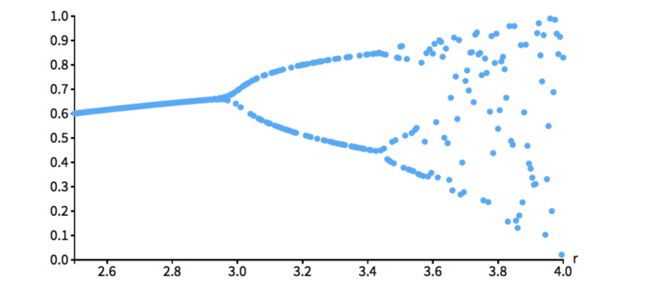
花一些额外的功夫,我们可以视觉化单峰映像的混沌二根分支。
func logisticMap(r: Double) -> RecurrenceRelation
{
return RecurrenceRelation([0.5]) { x, n in
r * x[n-1] * (1 - x[n-1])
}
}
for r in stride(from: 2.5, to: 4, by: 0.005) {
var map = logisticMap(r)
for _ in 1...50 { map.next() }
// 处理一些得到的值
Array(map.prefix(10))[Int(arc4random_uniform(10))]
// 随机选择接下来 10 个值当中的一个
}
相关推荐
TED 演讲,The magic of Fibonacci numbers, 演讲者,Arthur Benjamin.
Binet's Formula, 使用一个几乎常量时间的公式来计算斐波那契数。
Arrays, Linked Lists, and Performance,作者 Airspeed Velocity, 对序列使用其他有意思的方法,包括对ManagedBuffer的讨论。
本文由 SwiftGG 翻译组翻译,已经获得作者翻译授权,最新文章请访问 http://swift.gg。