第八章 提升方法
提升方法 (Boosting)
Boosting基本思想: 通过改变训练数据的概率分布(训练数据的权值分布),学习多个弱分类器,并将它们线性组合,构成强分类器。
Boosting 方法需要解决两个问题
- 如何改变训练数据的权值
- 如何将弱分类器组合成强分类器。
AdaBoost 思想
1.提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。
未被正确分类的样本受到后一轮弱分类器更大的关注。
2. AdaBoost 采用加权多数表决,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用。
AdaBoost 算法
考虑二分类问题
数据集 T ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . ( x n , y n ) T{(x_1,y_1),(x_2,y_2),...(x_n,y_n)} T(x1,y1),(x2,y2),...(xn,yn) , y i ∈ { 0 , 1 } y_i \in \{0,1\} yi∈{0,1}
有M个弱分类器 G m ( x ) , m = 1 , 2 , . . M G_m(x) , m=1,2,..M Gm(x),m=1,2,..M。
(1)初始化训练数据 的权值分布
D 1 = ( w 11 , . . w i 1 , . . . , w 1 N ) , w 1 i = 1 N , i = 1 , 2 , . . , N D_1=(w_{11},..w_{i1},...,w_{1N}) , w_{1i}=\frac{1}{N}, i=1,2,..,N D1=(w11,..wi1,...,w1N),w1i=N1,i=1,2,..,N
(2)for m = 1 to M
(a) 使用具有权值分布 D m D_m Dm的数据训练数据集学习,得到基本分类器 G m ( x ) G_m(x) Gm(x)。
这个分类器是使得第m轮加权训练数据分类误差率最小的基本分类器
(b)计算分类误差率
e m = P ( G m ( x ) ̸ = y i ) = ∑ i = 1 N w m i I ( G m ( x ) ̸ = y i ) e_m = P(G_m(x) \not= y_i) = \sum_ {i=1}^Nw_{mi}I(G_m(x) \not= y_i) em=P(Gm(x)̸=yi)=i=1∑NwmiI(Gm(x)̸=yi)
(c)计算 G m ( x ) G_m(x) Gm(x)的系数
a m = 1 2 l n 1 − e m e m a_m = \frac{1}{2}ln\frac{1-e_m}{e_m} am=21lnem1−em
(d)更新训练数据的权值分布
D m + 1 = ( w m + 1 , 1 , . . . w m + 1 , i , . . . w m + 1 , N ) D_{m+1} = (w_{m+1,1},...w_{m+1,i},...w_{m+1,N}) Dm+1=(wm+1,1,...wm+1,i,...wm+1,N)
w m + 1 , i = w m i Z m e x p ( − α m y i G m ( x i ) ) , i = 1 , 2 , . . N w_{m+1,i}= \frac{w_{mi}}{Z_m}exp(- \alpha_my_iG_m(x_i)),i=1,2,..N wm+1,i=Zmwmiexp(−αmyiGm(xi)),i=1,2,..N
Z m Z_m Zm是规范化因子
Z m = ∑ i = 1 N w m i e x p ( − α m y i G m ( x i ) ) Z_m=\sum_{i=1}^Nw_{mi}exp(- \alpha_my_iG_m(x_i)) Zm=i=1∑Nwmiexp(−αmyiGm(xi))
(3)构建基本分类器的线性组合
f ( x ) = ∑ m = 1 M α m G m ( x ) f(x)= \sum_{m=1}^M\alpha_mG_m(x) f(x)=m=1∑MαmGm(x)
得到最终的分类器
G ( x ) = s i g n ( f ( x ) ) = s i g n ( ∑ m = 1 M α m G m ( x ) ) G(x) = sign(f(x)) = sign(\sum_{m=1}^M\alpha_mG_m(x)) G(x)=sign(f(x))=sign(m=1∑MαmGm(x))
AdaBoost 算法的理解
- (2)(b)权值的分布影响体现在损失函数上?基学习器是朝着最小化损失函数去学习的,被误分的样本具有更大的权值,因此受到了“更大的关注”。
- (2)(c)基学习器的系数,它是由最小化指数损失函数得到的,(后面会提到的前向分步算法)
先直观理解
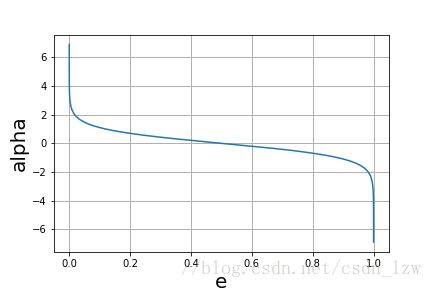
e m ≤ 1 2 e_m\le\frac{1}{2} em≤21时, α m ≥ 0 \alpha_m\ge0 αm≥0,并且 α m \alpha_m αm随着分类误差率的减小而增大。
误分类率小的系数大,即在最后加权表决时起到较大的作用。
系数的另一个作用,改变权值分布(2)(d),扩大误分样本权值,缩小被正确分类的样本。 - (3)基分类器线性组合的系数 α m \alpha_m αm之和不为1;
二分类的输出为{-1,+1},1多时,多数表决为1,求和大于0,因此用符号函数。 - AdaBoost 最基本的性质是它能在学习过程中不断减少训练误差,即在训练数据集上的分类误差率
AdaBoost 的另一种解释
模型:加法模型
策略:最小化损失函数(指数函数)
算法:前向分步算法
前向分步算法
加法模型
f ( x ) = ∑ m = 1 N β m b ( x ; γ m ) f(x) = \sum_{m=1}^N\beta_mb(x;\gamma_m) f(x)=m=1∑Nβmb(x;γm)
其中, b ( x ; γ m ) b(x;\gamma_m) b(x;γm)为基函数, γ m \gamma_m γm为基函数的参数, β m \beta_m βm为基函数的系数。
给定训练数据及损失函数 L ( y , f ( x ) ) L(y,f(x)) L(y,f(x))的条件下,学习加法模型 f ( x ) f(x) f(x)成为经验风险最小化问题
m i n β m , γ m ∑ i = 1 N L ( y i , ∑ m = 1 M β m b ( x i ; γ m ) ) \mathop {min}_{\beta_m,\gamma_m}\sum_{i=1}^{N}L(y_i,\sum_{m=1}^M\beta_mb(x_i;\gamma_m)) minβm,γmi=1∑NL(yi,m=1∑Mβmb(xi;γm))
前向分步算法思想:从前向后,每一步只学习一个基函数及其系数,逐步逼近优化上式目标函数。
每一步只需要优化如下损失函数
m i n β , γ ∑ i = 1 N L ( y i , β b ( x i ; γ ) ) \mathop {min}_{\beta,\gamma}\sum_{i=1}^{N}L(y_i,\beta b(x_i;\gamma)) minβ,γi=1∑NL(yi,βb(xi;γ))
Adaboost 是前向分步算法的特例,模型是由基本分类器组成的加法模型,损失函数是指数函数
L ( y , f ( x ) ) = e x p [ − y f ( x ) ] L(y,f(x)) = exp[-yf(x)] L(y,f(x))=exp[−yf(x)]
根据前向分步算法,可以把 α m \alpha_m αm和 G m ( x ) G_m(x) Gm(x)推导出来对应到开头的AdaBoost
证明 蓝皮书


这个博客的例子讲解很详细
http://blog.csdn.net/mousever/article/details/52038198