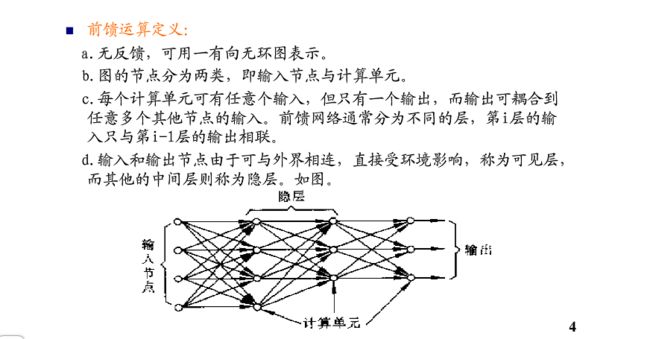
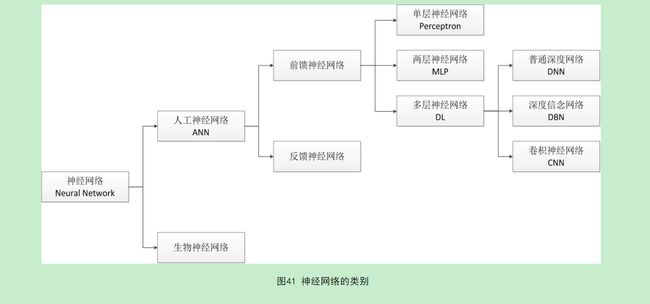
多层神经网络ANN

本文基于 cnblog学习总结，基于的博客地址如下： http://www.cnblogs.com/ronny/p/ann_02.html

在实际应用过程中，单个神经元不能拟合太复杂的映射关系，我们需要构建更复杂的网络来逼近那些更复杂的目标函数。使用多层网络有时可以经过更少的迭代训练就能找到很好的收敛关系。

多层神经网络是由多个层结构组成的网络系统，他的每一层都是若干个神经元结点构成，该层的任意一个结点都与上一层的每一个结点相连，由他们提供输入，经过计算产生该结点的输出，并作为下层结点的输入。
任何多层的网络结构必须有一输入层、一个输出层。

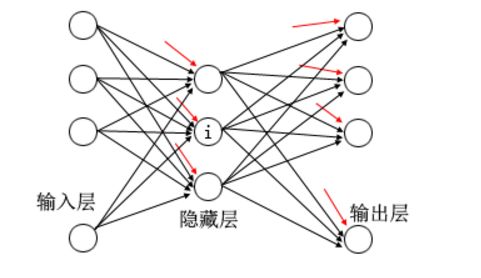
输入层的每一个结点就是一个原始数据。

什么类型的函数可以使用多层网络来表示呢？或者说什么样的分类问题可以用多层网络来表示呢？答案是：任意函数。任意函数可以被一个有三层单元的网络以任意精度逼近(Cybenko 1988)。但是值得注意的是，我们使用的梯度下降算法并没有搜索整个权值空间，所以我们很可能会漏掉那个最合适的权值集合。

过度拟合

因为我们收集到的样本中有些样本可能由于我们分类错误等原因，造成了一个错误的样本用例，实际上神经网络对这种带有噪点的样本的适应性很强。但是在上面我们介绍的原理中，我们并没有规定权值迭代更新的终止条件，往往我们是设置了一个迭代次数来控制，也就有可能造成，在训练的后期那些权值是过度拟合那些噪点样本。这个问题没有统一的解决方案，现在比较常用的方法就是通过交叉验证，即在训练的同时，用一组校验校本进行测试，找出分类率回降的一个点，从而终于训练过程。

下面我们考虑这个问题，对于多层（以两层为例—一个隐藏层和一个输出层）神经网络，为什么可以拟合非线性的数据关系？并且已经证明，两层神经网络可以拟合任意的函数，给出任意的决策分界面。

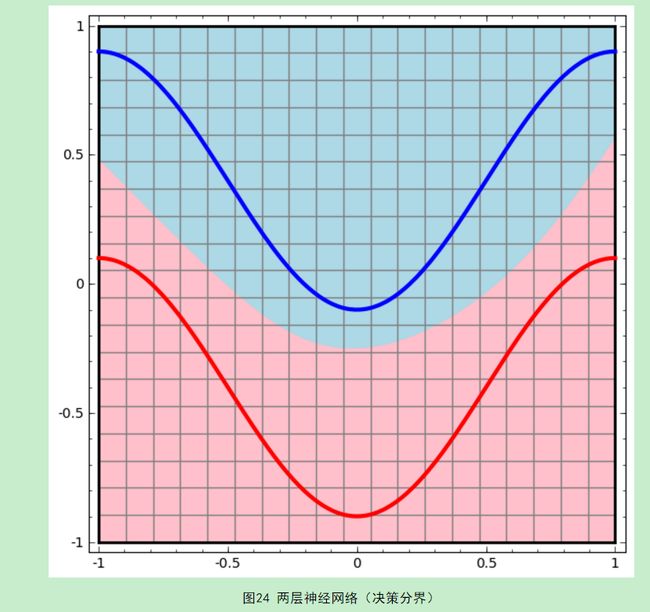
单层的只能画出线性的决策面哦。

事实上，输出层的决策分界仍然是直线（应该是一个n-1超平面），但是，从输入层到隐藏层，数据发生了空间变换。也就是说，两层神经网络中，隐藏层对原始的数据进行了一个空间变换，使其可以被线性分类，然后输出层的决策分界划出了一个线性分类分界线，对其进行分类。

这样就导出了两层神经网络可以做非线性分类的关键–隐藏层。一次隐藏层就是对向量的空间坐标进行了一次变换。因此，隐藏层的参数矩阵就是使得数据的原始坐标空间从线性不可分，转化为线性可分。

下面我们看隐藏层的节点数设计。实际上，在设计一个神经网络时，输入层的节点数需要与特征的维度匹配，输出层的结点数要与目标维度匹配。而中间层的节点数，则是设计者自己指定。如何决定这个自由层的节点数呢？目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值，通过切换这几个值来看整个模型的预测效果，选择效果最好的值作为最终选择。这种方法又叫做Grid Search（网格搜索）。

这个是从easy-pr上截取的图像，说明的含义就是每一个输入的是120维的特征向量。输出的是要预测的文字类别一共包含了英文字母+地区简称（湘、鄂等）。这个40个隐层结点是通过测试，发现在整个网络测试中，这个结果比较好。

• 卷积神经网络
  卷积神经网络将深度学习的思想引入到了神经网络中，通过卷积运算来由浅入深的提取图像的不同层次的特征，而利用神经网络的训练过程让整个网络自动调节卷积核的参数，从而无监督的产生最适合的分类特征。

根据深度学习关于人的视觉分层的理论，人的视觉对目标的辨识是分层的，低层会提取一些边缘特征，然后高层进行形状或目标的认知，更高层的会分析一些运动和行为。也就是说高层的特征是低层特征的组合，从低层到高层的特征表示越来越抽象，越来越能表现语义或者意图。而抽象层面越高，存在的可能猜测就越少，就越有利于分类。

深度学习就是通过这种分类的自动特征提取来达到目标分类，先构建一些基本的特征层，然后用这些基础特征去构建更高层的抽象，更精确的分类特征。

整个卷积神经网络的结构也就比较容易理解了，他在普通的多层神经网络前面加了2层特征层，这两层特征层是通过权重可调整的卷积运算实现的。

与普通多层神经网络不同的是，卷积神经网络里，有特征抽取层与降维层，这些层的结点连结是部分连接且，一幅特征图由一个卷积核生成，这一幅特征图上的所有结点共享这一组卷积核的参数。

比如我们设计一个5层的卷积神经网络，一个输入层，一个输出层，2个特征提取层，一个全连接的隐藏层。下面详细说明每一层的设计思路。

在一般的介绍卷积神经网络的文章中你可能会看到在特征层之间还有2层降维层，在这里我们将卷积与降维同步进行，只用在卷积运算时，遍历图像中像素时按步长间隔遍历即可。（也即是 Feature Maps—降维—–Feature Maps—–降维）

输入层：普通的多层神经网络，第一层就是特征向量。一般图像经过人为的特征挑选，通过特征函数计算得到特征向量，并作为神经网络的输入。而卷积神经网络的输出层则为整个图像，如上图示例29*29,那么我们可以将图像按列展开，形成841个结点。而第一层的结点向前没有任何的连结线。（卷积神经网络没有自己提取特征的过程）

第1层：第1层是特征层，它是由6个卷积模板与第一层的图像做卷积形成的6幅13*13的图像。也就是说这一层中我们算上一个偏置权重，一共有只有（5*5+1）*6=156权重参数，但是，第二层的结点是将6张图像按列展开，即有6*13*13=1014个结点。

而第2层构建的真正难点在于，连结线的设定，当前层的结点并不是与前一层的所有结点相连，而是只与25邻域点连接，所以第二层一定有（25+1）*13*13*6=26364条连线，但是这些连结线共享了156个权值。按前面多层网络C++的设计中，每个连线对象有2个成员，一个是权重的索引，一个是上一层结点的索引，所以这里面要正确的设置好每个连线的索引值，这也是卷积神经网络与一般全连结层的区别。

第2层：第2层也是特征层，它是由50个特征图像组成，每个特征图像是5*5的大小，这个特征图像上的每一点都是由前一层6张特征图像中每个图像取25个邻域点最后在一起加权而成，所以每个点也就是一个结点有（5*5+1）*6=156个连结线，那么当前层一共有5*5*50=1250个结点，所以一共有195000个权重连结线，但是只有（5*5+1）*6*50=7800个权重参数，每个权重连结线的值都可以在7800个权重参数数组中找到索引。

所以第3层的关键也是，如何建立好每根连结线的权重索引与与前一层连结的结点的索引。

第3层：和普通多神经网络没有区别了，是一个隐藏层，有100个结点构成，每个结点与上一层中1250个结点相联，共有125100个权重与125100个连结线。

第4层：输出层，它个结点个数与分类数目有关，假设这里我们设置为10类，则输出层为10个结点，相应的期望值的设置在多层神经网络里已经介绍过了，每个输出结点与上面隐藏层的100个结点相连，共有（100+1）*10=1010条连结线，1010个权重。

　　在深度学习中，泛化技术变的比以往更加的重要。这主要是因为神经网络的层数增加了，参数也增加了，表示能力大幅度增强，很容易出现过拟合现象。因此正则化技术就显得十分重要。目前，Dropout技术，以及数据扩容（Data-Augmentation）技术是目前使用的最多的正则化技术。