算法 | k-means聚类

概要： 本文将要介绍机器学习的一种常见算法：k-means聚类。聚类属于无监督学习，相比于分类，聚类不依赖预定义的类和类标号的训练实例。由于k-means聚类比较简单，所以我主要介绍在写相关代码时的体验。代码仍是用MATLAB写的。
关键字： k-means聚类算法; MATLAB
 

1 背景说明

   k-means聚类可以说是大名鼎鼎了，应该算是最常用的聚类方法之一。第一次听到此概念是在大三下学期的语音信号处理课程上，当时讨论的是说话人识别问题。最近在恰好又在Stanford课程EE103的教材上看到了这个问题，于是就尝试了一下。

   我在学习算法时有一个习惯，就是喜欢自己动手编程。由于k-means非常常用，所以很多软件都会有相关函数，MATLAB当然也不例外，它自带的函数名叫kmeans，很容易就能调用。但是我还是自己动手写了，也算是顺便复习一下MATLAB编程吧。

   最后还是想安利一下EE103这门课，尤其是它的配套教材，从向量说起，然后延伸到矩阵，最后讲到最小二乘。这本书语言清晰、讲解生动、示例丰富、深入浅出，是预习、学习、复习线性代数及其周边知识的绝佳教材，比国内那些乱七八糟的教科书不知道高到哪里去了。

2 算法原理

2.1 什么是聚类

   所谓聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇，或一个类。

2.2 k-means聚类原理

   由于我很懒，不想敲公式，也懒得重复已经弄懂的知识点，emmm……所以很抱歉，这方面的知识请查阅其他相关资料。

3 程序实现

   Talk is cheap. Just see my code!

   首先请看我的代码文件目录：

图1 算法所需文件目录

 
   这里一共有9个.m源文件，每个文件内各有一个函数，都是运行算法所必备的。其中倒数第二个mykmeans.m是主要代码，其他8个函数都是通过mykmeans.m调用的。

   下面是我给kmeans函数所做的功能定义：

function varargout = mykmeans(X,k,varargin)
%MYKMEANS - K-means clustering.
%   To divide the input data into k classes using the k-means algorithm.
%   
%   Idx = mykmeans(X,k)
%   Idx = mykmeans(X,k,DIM)
%   Idx = mykmeans(X,k,DIM,errdlt)
%   Idx = mykmeans(X,k,DIM,errdlt,replicates)
%   Idx = mykmeans(X,k,DIM,errdlt,replicates,Cin)
%   [Idx,C,sumD,D,Errlist] = mykmeans(...)
%   [...] = mykmeans(...,'Param1','Param2'...)  
% 
%   Input - 
%   X:          the input N*P matrix X with N points of P-dimension;
%   k:          the number of classes;
%   DIM:        1-the number of rows represents the number of points;
%               2-the number of columns represents the number of points;
%   errdlt:     the error between the last cluster and current cluster
%               that stops clustering;
%   replicates: the number of repeated clusters;
%   Cin:        the number of repeated clusters;
%   Param1:     distance
%   Val1:       sqEuclidean:    欧氏距离
%               cityblock:      曼哈顿距离
%               cosine:         余弦距离-针对向量
%               correlation:    相关距离
%               Hamming:        汉明距离-针对字符串和数字量(整数)
%   Param2:     start
%   Val2:       sample:         随机选取
%               plus  :         尽可能远选取-kmeans++
%               canopy:         (没有实现-因存在人为经验阈值故不适合)
%               matrix:         直接输入
%   Output - 
%   Idx:        a N*1 vector containing the cluster number of each point;
%   C:          a k*P matrix containing the coordinate of k cluster centers;
%   sumD:       a k*1 vector containing the sum of distances between every cluster
%               center and its within-cluster points;
%   D:          a N*k vector containing the distance between each point and each
%               cluster center;
%   Errlist:    a vector containing the clusting error after each round.

   从中可见我一共定义了8个输入参数、4个输出参数。其中输入参数有6个是可选的，输出参数都是可选的。用户可以选择聚类中心初始化的方式——包括随机选择、使用kmeans++方法选择以及指定初始中心三种，和聚类的距离测度——包括欧氏距离、曼哈顿距离、余弦距离、相关距离和汉明距离。当然其中某些选项存在限制。

   其他的一些输入输出参数我都是参照MATLAB自带的函数kmeans进行命名的，但是内部的代码两者差异巨大，风格也不一样，不过我始终觉得我的代码比较容易读懂一点hhh(此处似乎有点王婆卖瓜自卖自夸的嫌疑orz…)。

   这是一个有2个环节互相循环的算法，所以一定要先给一个初始化的条件。一般来说，会先给出一组聚类中心。下面是给出初始化聚类中心的代码。

%% 确定初始化矩阵-初始中心
if strcmpi(start,'matrix')
    % 使用特定的K个点
    C = Cin;
elseif strcmpi(start,'sample')
    % 随机选择K个点-default
    Idx = randperm(N);
    Idx = Idx(1:k);
    C = X(Idx,:);
elseif strcmpi(start,'plus')
    % 选择彼此距离尽可能远的K个点
    C = mycluster_plus(X,k);
elseif strcmpi(start,'canopy')
    % canopy算法初始化
    error('Error! Change another method.');        % emmm 这个方法暂时没有做
end

   接下来就是根据这一组中心确定各个点的所属，并求出初始条件下的聚类误差。注意，这里有多种距离测度，包括欧氏距离、曼哈顿距离、余弦距离等，用户可以在入口参数处进行选择。关于这些距离的内容，这个博客讲解得比较清楚。下面是确定初始分类，并求初始误差的代码。

%% 确定初始分类，并求初始误差
% 给X额外加了1列，在一次程序中只允许运行1次
if size(X,2)==P
    X = [X,zeros(N,1)];
else
    error('Error! X alreadly has %d columns.',P);
end
% 确定初始分类
for i=1:N
    temp = repmat(X(i,1:P),k,1);            % 拓展成k行方便相减
    dists = mydist(distance,temp,C);
    [~,X(i,P+1)] = min(dists);            % 取距离最小的,dists:k*1
end
% 求初始误差
err_init = myerrcal(distance,X,C);
fprintf('初始聚类误差为%d.\n',err_init);

   接下来是一个巨大的循环，要考虑到用户对循环次数、最小循环误差的设定，需要判断的情况还挺多，不过总的来说内容是确定的，就是进入“计算聚类中心-确定各点所属-计算聚类误差-判断是否结束”的循环。下面是循环聚类的代码。

%% 进入"中心-分类-求误差"循环
err = err_init;
T=1;
if limit_exist==0
    while(1)
        % 已知分类求新中心C-质心运算
        C = zeros(k,P);
        n = zeros(k,1);
        for i=1:N
            g_num = X(i,P+1);
            C(g_num,:)=( C(g_num,:)*n(g_num)+X(i,1:P) ) / (n(g_num)+1);
            n(g_num) = n(g_num)+1;
        end
        % 已知中心确定分类
        for i=1:N
            % 拓展成k行方便相减
            temp = repmat(X(i,1:P),k,1);          
            % 距离测度
            dists = mydist(distance,temp,C);
            % 取距离最小的
            [~,X(i,P+1)] = min(dists);            
        end
        
        % 确定分类后计算误差
        err_temp = myerrcal(distance,X,C);
        fprintf('第%d轮聚类误差为%d.\n',T,err_temp);
        T=T+1;
        
        % 绘制图像-仅用于调试，实际使用时为运算速度计应注释
        mydrawkmeans(X,C);
        % 误差列表增加一项
        err = [err;err_temp];
        % 设置退出条件
        if ( abs(err(end-1)-err(end))

   代码的主要部分其实就这些内容，其他还有需要注意的地方有：
   1-中间调用了其他8个文件里的函数，读者在使用时注意不要遗漏；
   2-输入输出参数比较复杂，还涉及字符串的输入，所以函数前部的准备代码也花了一百多行，读者如有兴趣也可以研究一下。

4 结果分析

   现在让我们来测试这个算法的性能。

4.1 随机生成初始聚类中心

   首先生成随机的数据点如图2所示：

图2 生成的245个随机数据点

 
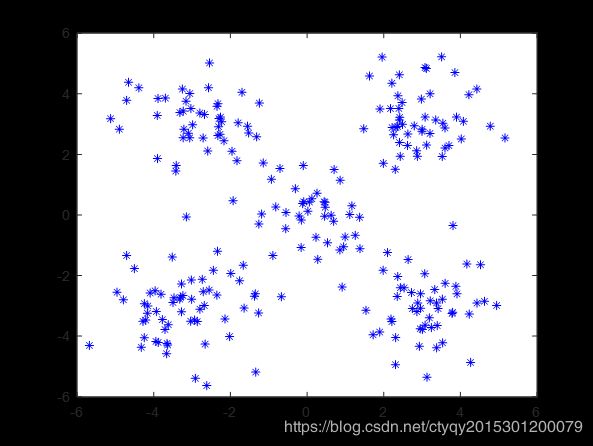
   显然，人眼看来这些点可以分为5簇，即左上、右上、左下、右下、中间。现在来看算法的表现，在将类别数设置为5、距离测度选为欧氏距离、随机选取初始聚类中心、不设聚类循环上限、设置最小误差变化为1的情况下，某一次聚类的过程如图3所示。

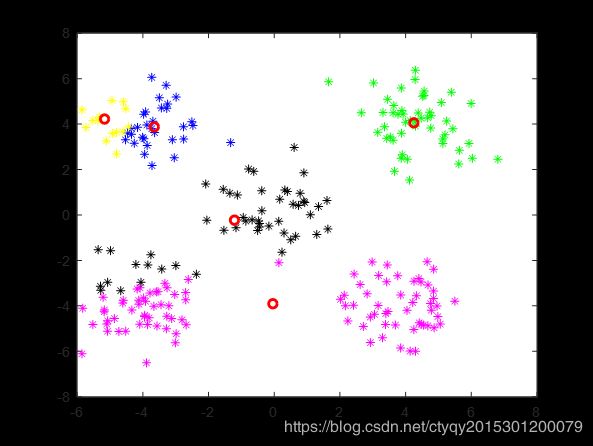第1轮

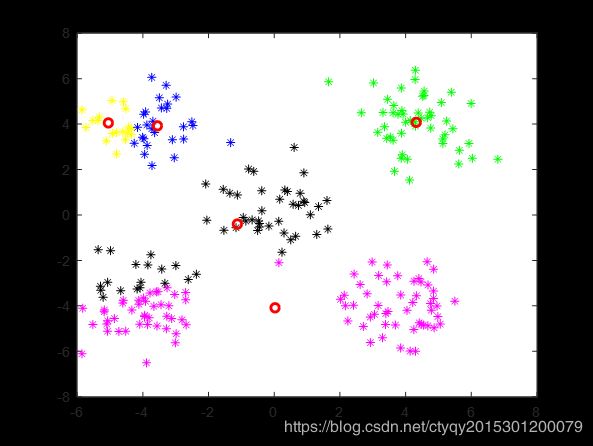第2轮

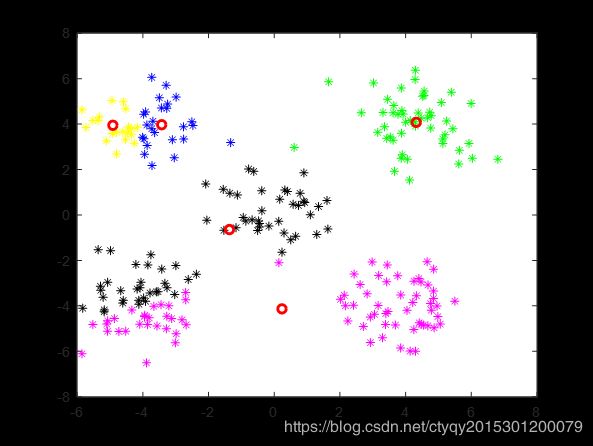第3轮

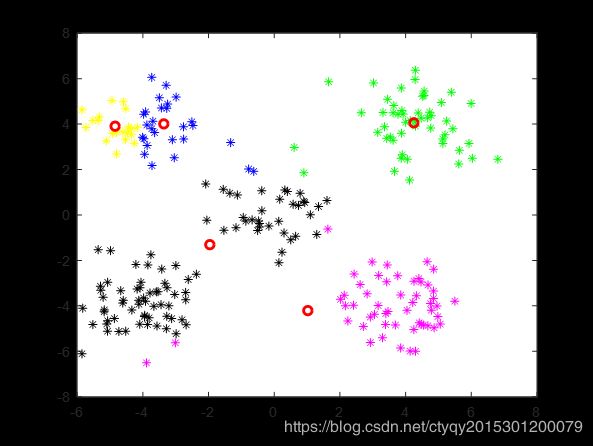第4轮

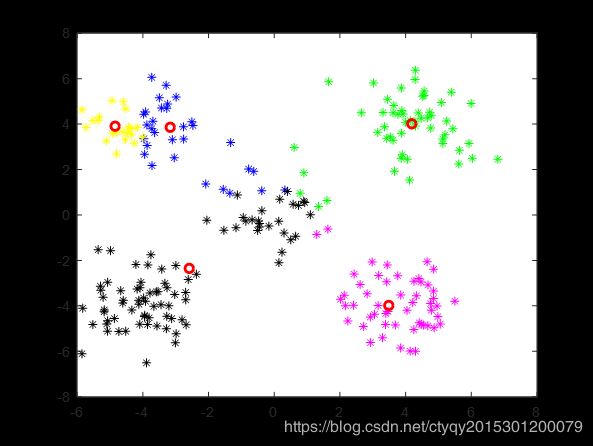第5轮

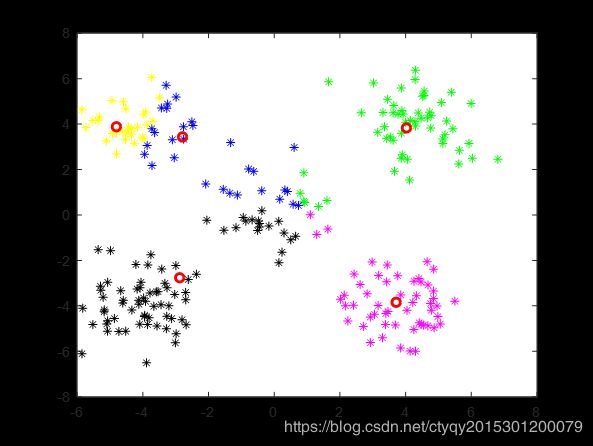第6轮

第7轮

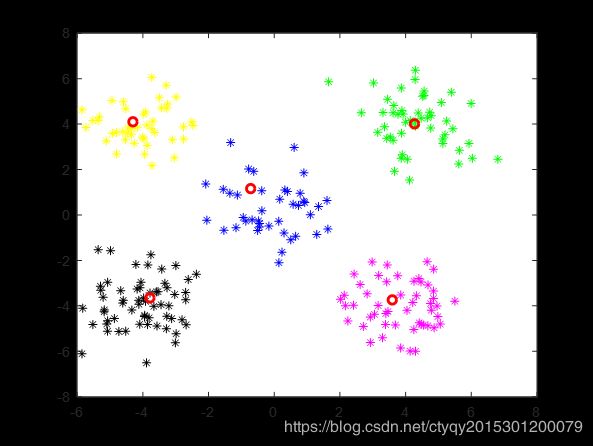第8轮

第9轮

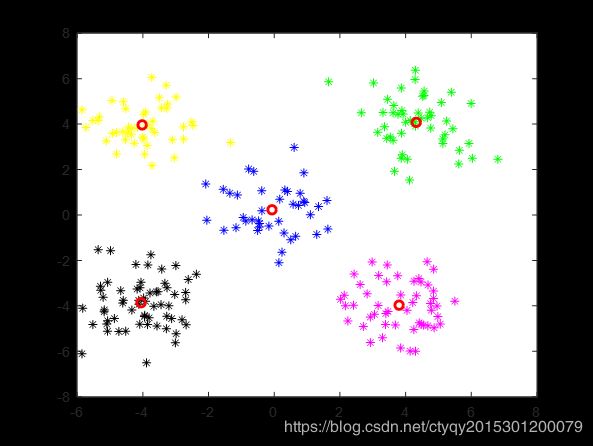第10轮

图3 某次聚类过程及结果

 
   算法在10轮后停止更新，即点数分组趋于稳定。通过图4的命令行窗口我们可以看到在这个过程中误差的变化。可见在第9轮和第10轮之间聚类误差的变化量小于1，说明已经基本达到了聚类的目的，再继续循环下去也没有了必要。

图4 聚类误差在每轮聚类后的变化

 

4.2 kmeans++算法生成初始聚类中心

   上面的结果是在随机选择初始化聚类中心的情况下进行的，根据我多次试验的发现，若采用kmeans++确定初始中心，那么聚类所需要的轮数会大大降低，大部分情况下5次以内即可解决战斗。某一次初始化中心如图5所示。

图5 kmeans算法生成的初始聚类中心

 
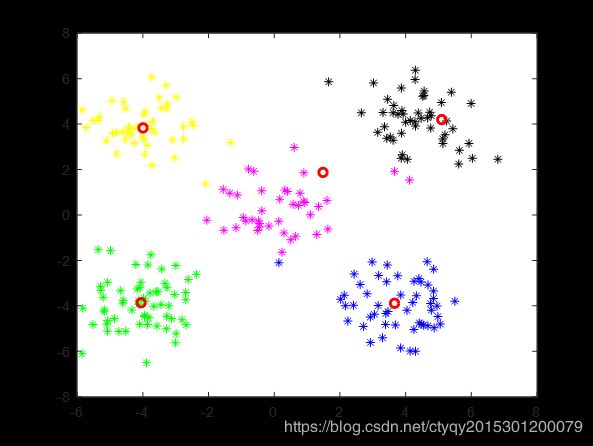
   可见初始聚类就已十分接近正确答案。这次实验仅3次聚类就得到了稳定的结果。

4.3 不正确的情形

   那么这样聚类会不会出现不正确的答案呢？答案是肯定的。图6展示了其中的2种情况翻了车的情况。值得一提的是这两次翻车都是出现在初始聚类中心随机选取的情况下，而用kmeans++获取的初始聚类中心则比较难以得到非正确结果，这又进一步表明了初始聚类中心选取的重要性。

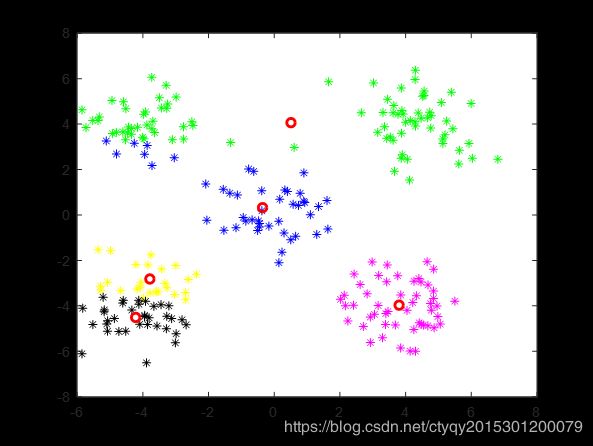情形一

情形二

图6 聚类结果不正确的情形

4.4 其他情形

   在这个实验中人眼明显感觉分成5类是正确的，可是很多情况下分类数 目是未知的，那就只能用各种方法去猜测。下面讨论分类数未知时kmeans算法的表现。

   对一个实际分类数为5的数据集，在分别猜测分类数目为3、4、6、7时的分类结果如图7所示。

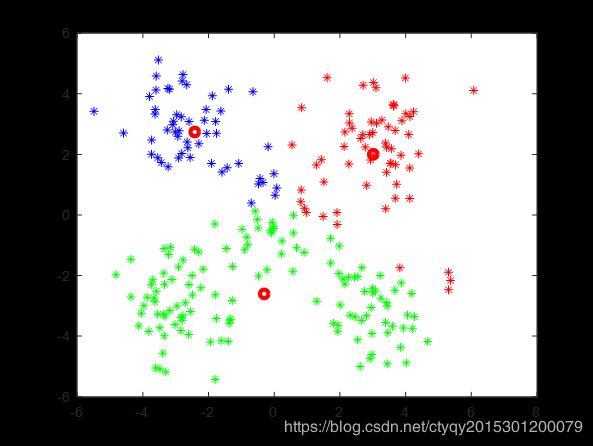猜测分类数目为3

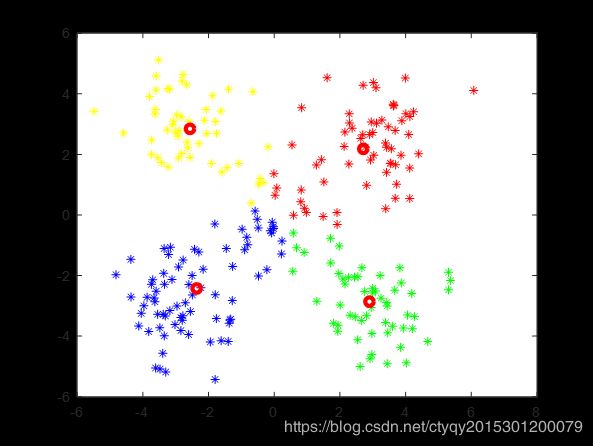猜测分类数目为4

猜测分类数目为6

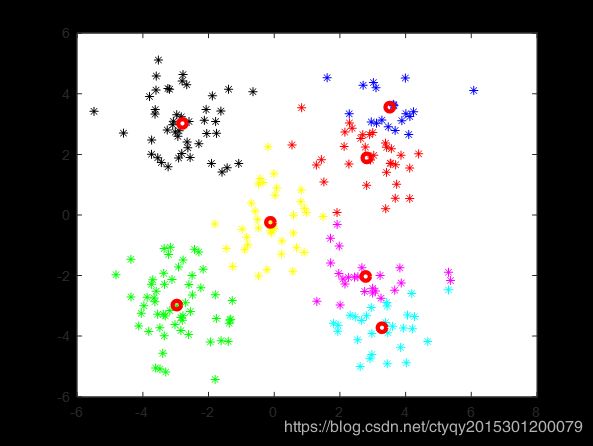猜测分类数目为7

图7 猜测分类数不等于实际分类数的情形

 
   甚至于在猜测分类数和实际分类数大相径庭时，kmeans算法也总能给出一个结果——不论这个给出的结果是否具有真正意义上的合理性。如图8所示。

图8 猜测分类数为15而实际分类数为5

 
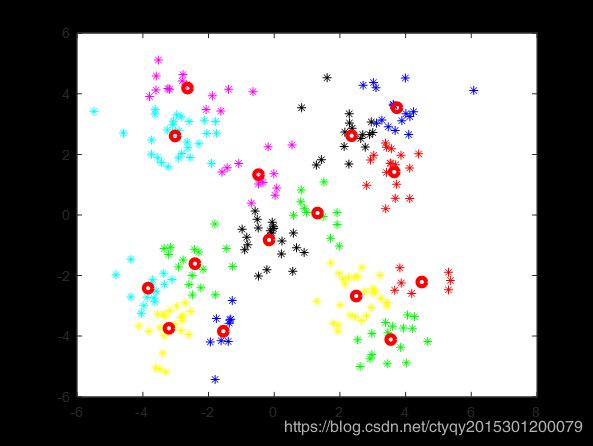
   很难说这到底算是优点还是缺点。因为一方面，在很多情况下先验知识不能告诉我们到底该分为几类，这时猜测的分类数和实际分类数难免不相同，所以需要在这种不相同情况下给出结果；但是另一方面，若猜测与实际偏差过大，这时kmeans算法所给出的结果往往就是带有误导性的，甚至是错误的。

   所以，kmeans一般情况下应用在分类数目已知的情况下，比如0-9手写体识别、语音性别识别、说话人数已知的说话人识别等。如果非要猜测，可以采用一个叫做canopy聚类的初始化方法，它可以在不知分类数目的情况下给出大致的初始化聚类中心，而且和实际的分类数目相差不多。canopy聚类的基本思想是，先把待分类对象按照疏密关系大致分为若干类，再在各类中随机抽出一个代表向量。但是，canopy聚类算法中有两个人为定义的经验阈值T1和T2，也都需要一定程度的先验知识。T1和T2简单来说就是度量类内疏密程度和类间疏密程度的两个参量，若要深入了解，可以去了解一下canopy聚类算法。

5 后记

   本文只是简单介绍了kmeans算法的原理和MATLAB实现，而且实验也只是对二维平面上的点做了聚类。接下来我将会把kmeans聚类的方法用在我之前做过的0-9数字手写体识别和语音性别识别这两个小项目上，这两个我之前都是用的朴素贝叶斯分类器来做的，之后我也将针对朴素贝叶斯和kmeans聚类这两种方法做一些分析和比较。

   转载时务必注明来源及作者。尊重知识产权从我做起。

   代码已上传至网络，欢迎下载，密码是xl94。