学习:词嵌入向量WordEmbedding
复制链接
词嵌入向量(WordEmbedding)是NLP里面一个重要的概念,我们可以利用WordEmbedding将一个单词转换成固定长度的向量表示,从而便于进行数学处理。本文将介绍WordEmbedding的使用方式,并讲解如何通过神经网络生成WordEmbedding。
WordEmbedding的使用
使用数学模型处理文本语料的第一步就是把文本转换成数学表示,有两种方法,第一种方法可以通过one-hot矩阵表示一个单词,one-hot矩阵是指每一行有且只有一个元素为1,其他元素都是0的矩阵。针对字典中的每个单词,我们分配一个编号,对某句话进行编码时,将里面的每个单词转换成字典里面这个单词编号对应的位置为1的one-hot矩阵就可以了。比如我们要表达“the cat sat on the mat”,可以使用如下的矩阵表示。
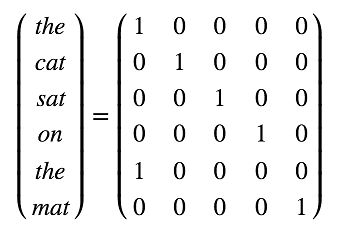
one-hot表示方式很直观,但是有两个缺点,第一,矩阵的每一维长度都是字典的长度,比如字典包含10000个单词,那么每个单词对应的one-hot向量就是1X10000的向量,而这个向量只有一个位置为1,其余都是0,浪费空间,不利于计算。第二,one-hot矩阵相当于简单的给每个单词编了个号,但是单词和单词之间的关系则完全体现不出来。比如“cat”和“mouse”的关联性要高于“cat”和“cellphone”,这种关系在one-hot表示法中就没有体现出来。
WordEmbedding解决了这两个问题。WordEmbedding矩阵给每个单词分配一个固定长度的向量表示,这个长度可以自行设定,比如300,实际上会远远小于字典长度(比如10000)。而且两个单词向量之间的夹角值可以作为他们之间关系的一个衡量。如下表示:
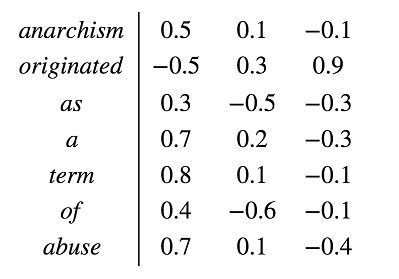
通过简单的余弦函数,我们就可以计算两个单词之间的相关性,简单高效:
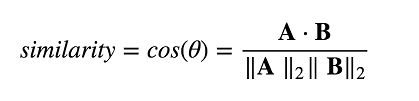
两个向量相关性计算
因为WordEmbedding 节省空间 和 便于计算 的特点,使得它广泛应用于NLP领域。接下来我们讲解如何通过神经网络生成WordEmbedding。
复制链接2
一、数学上的“嵌入”(Embedding)
Embed这个词,英文的释义为, fix (an object) firmly and deeply in a surrounding mass, 也就是“嵌入”之意。例如:One of the bullets passed through Andrea’s chest before embedding itself in a wall.
另外,这个词(的分词形式)在数学上也是一个专有名词,Embedding,它广泛存在于包括代数、拓扑与几何等诸多数学领域。它主要表征某个数学结构中的一个实例被包含在另外一个实例中,例如一个group它同时又是一个subgroup。
当我们说某个对象 X 被嵌入到另外一个对象 Y 中, 那么 embedding 就由一个单射的、结构保持的(structure-preserving)映射 f : X → Y 来给定的。此处的结构保持的具体含义要依赖于X 和 Y 是哪种数学结构的实例而定。
举个例子:我们可以把整数“嵌入”进有理数之中。显然,整数是一个group,同时它又是有理数的一个subgroup。整数集合中的每个整数,在有理数集合中都能找到一个唯一的对应(其实就是它本身)。同时,整数集合中的每个整数所具有的性质,在有理数中同样得到了保持。同理,我们也可以把有理数“嵌入”到实数中去。
二、词嵌入(Word Embedding)
前面我们之所以要讨论Embedding在数学上的意思,就是因为这名称其实特别具有一种误导性,尤其是在翻译成中文的时候会令汉语思维下的我们更加难于把握住它的本质。
Word Embedding并不是要把单词像贴瓷砖那样镶嵌进什么地方。更重要的是,我们在把单词嵌入进另外一个空间时,要做到单射和structure-preserving,或者说我们更专注的是映射关系,而最终得到每个单词在另外一个空间中的表达也仅仅是之前设计好的映射关系的很自然的表达。
Word embedding 是NLP中一组语言模型(language modeling)和特征学习技术(feature learning techniques)的总称,这些技术会把词汇表中的单词或者短语(words or phrases)映射成由实数构成的向量上。
最简单的一种Word Embedding方法,就是基于词袋(BOW)的One-Hot表示。这种方法,把词汇表中的词排成一列,对于某个单词 A,如果它出现在上述词汇序列中的位置为 k,那么它的向量表示就是“第 k 位为1,其他位置都为0 ”的一个向量。
例如,有语料库如下:
John likes to watch movies. Mary likes movies too.
John also likes to watch football games.
把上述语料中的词汇表整理出来并排序(具体的排序原则可以有很多,例如可以根据字母表顺序,也可以根据出现在语料库中的先后顺序)
假设我们的词汇表排序结果如下:
{“John”: 1, “likes”: 2, “to”: 3, “watch”: 4, “movies”: 5, “also”:6, “football”: 7, “games”: 8, “Mary”: 9, “too”: 10}
那么则有如下word的向量表示:
John: [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
likes: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
……
此时,你也可以进一步地把文档也表示成向量。方法就是直接将各词的词向量表示加和,于是则有原来的两句话的向量表示如下:
[1, 2, 1, 1, 2, 0, 0, 0, 1, 1]
[1, 1, 1, 1, 0, 1, 1, 1, 0, 0]
One-hot方法很简单,但是它的问题也很明显:
1)它没有考虑单词之间相对位置的关系;
2)词向量可能非常非常长!
针对第一个问题,你可能会想到n-gram方法,这确实是一个策略,但是它可能会导致计算量的急剧增长。因为n-gram已经在之前的文章中解释过了,下面我们来看另外一个方法:共现矩阵 (Cocurrence matrix)。
一个非常重要的思想是,我们认为某个词的意思跟它临近的单词是紧密相关的。这是我们可以设定一个窗口(大小一般是5~10),如下窗口大小是2,那么在这个窗口内,与rests 共同出现的单词就有life、he、in、peace。然后我们就利用这种共现关系来生成词向量。

例如,现在我们的语料库包括下面三份文档资料:
I like deep learning.
I like NLP.
I enjoy flying.
作为示例,我们设定的窗口大小为1,也就是只看某个单词周围紧邻着的那个单词。此时,将得到一个对称矩阵——共现矩阵。因为在我们的语料库中,I 和 like做为邻居同时出现在窗口中的次数是2,所以下表中I 和like相交的位置其值就是2。这样我们也实现了将word变成向量的设想,在共现矩阵每一行(或每一列)都是对应单词的一个向量表示。
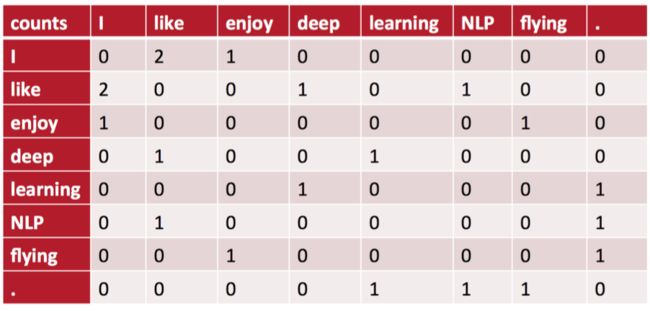
作为示例,我们设定的窗口大小为1,也就是只看某个单词周围紧邻着的那个单词。此时,将得到一个对称矩阵——共现矩阵。因为在我们的语料库中,I 和 like做为邻居同时出现在窗口中的次数是2,所以下表中I 和like相交的位置其值就是2。这样我们也实现了将word变成向量的设想,在共现矩阵每一行(或每一列)都是对应单词的一个向量表示。
虽然Cocurrence matrix一定程度上解决了单词间相对位置也应予以重视这个问题。但是它仍然面对维度灾难。也即是说一个word的向量表示长度太长了。这时,很自然地会想到SVD或者PCA等一些常用的降维方法。当然,这也会带来其他的一些问题,例如,我们的词汇表中有新词加入,那么就很难为他分配一个新的向量。但这并非本文要讨论的重点,我们不再赘述。
三、Word2Vec
我们已经见识了两种词嵌入的方式。而现在最常用、最流行的方法,就是Word2Vec。这是Tomas Mikolov在谷歌工作时发明的一类方法,也是由谷歌开源的一个工具包的名称。具体来说,Word2Vec中涉及到了两种算法,一个是CBOW一个是Skip-Gram。这也是因为深度学习流行起来之后,基于神经网络来完成的Word Embedding方法。
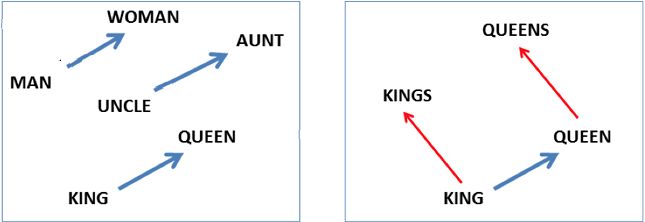
Word2Vec之所以现在这么流行,不同于之前的一些Word Embedding方法,它能够自动实现:1)单词语义相似性的度量;2)词汇的语义的类比。此处,语义的类比,反应的是类似下面这种关系:
- “国王” – “王后” ≈ “男” – “女”
- “英国” – “伦敦” ≈ “法国” – “巴黎” ≈ “首都”
如果用图形来表示,即如下图所示:
对于Skip-Gram模型来说,它是要Generates each word in context given centre word。如下图所示:

所以总概率定义为:
![]()
其中下标denotes position in running text. 对于每个单词而言,则有
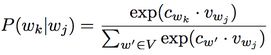
对于CBOW模型来说,Condition on context, and generate centre word。如下图所示:

要细抠Skip-Gram和CBOW的话,恐怕还需要很长篇幅和太多细节上的讨论,这一点留待后续文章中再来另行讨论。下面我们将在Python中实际使用一下Word2Vec,这就要简单许多了,因为我们可以直接使用gensim [1]。注意我们用来训练模型的语料库是NLTK中的Brown语料库。实际中要获得更高质量的模型,往往意味着需要更大的语料库,当然这也意味着更多的训练时间。