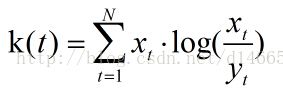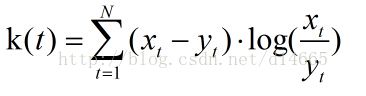模式识别中常用度量方式

1 欧式距离：

设X为N维列向量，y为其警戒距离，则：y=X‘*X。

 

2 Hausdorff距离：

设有两个向量集合，X={x1,x2,x3,x4,...xm}，Y={y1,y2,...yk}，其中集合内的每一个元素都是一个N维向量。

H(X,Y)代表集合X到集合Y的Hausdorff距离，它是一个单身距离。

H(X,Y)=max(x∈X) min(y∈Y) ||x-y||。

Hausdorff距离用如下步骤：（1）记录X集合中的每一个元素xi到离它最近的一个Y集合中的元素yi之间的距离；（2）找到这些距离的最大值。

需要注意的是：这个距离是单向的，即H(X,Y)！=H(Y,X)，如果想构造双向的Hausdorff距离，可以用如下形式：max(  H(X,Y),H(Y,X)  )。

PS：推荐使用双向的距离度量方式。

 

3 基于熵的度量：

设有两个向量X，Y。其中这两个向量都是N维的。

上述度量方式中是单向的，即X向量到Y向量的距离是不相同的。如果想构造双向的度量，可以用如下的公式：

 

4 Hanmming distance

汉明距离，即是两个字符串中，不同字符的个数，在图片检索中，通过粗量化，对图片特征进行聚类之后，可以再进行Hanmmind embedding算法，对同一个码字中的特征点，通过计算汉明距离，进行进一步量化。

 

5 直方图相交

假如有两个向量a = (a1,a2,a3,a4)，b = (b1,b2,b3,b4)。它们的直方图相关距离如下：

HI(a,b) = (min(a1,b1),min(a2,b2),min(a3,b3),min(a4,b4))。