图及其数据表示
文章目录
- 一、图形简介
- 1、图的相关概念
- (1)无向图
- (2)有向图
- 二、图的数据表示
- 1、邻接矩阵法
- 2、邻接表法
- 3、邻接矩阵法和邻接表法的demo:
一、图形简介
树状结构描述的是节点与节点之间的层次关系,但是图形结构主要是讨论两个节点之间“联通与否”的关系。
1、图的相关概念
图的定义:图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
(1)无向图
若顶点Vi到Vj之间的边没有方向,则称这条边为无向边,用无序偶对(Vi,Vj)来表示。如果图中任意两个顶点之间的边都是无向边,则称该图为无向图
。接下来介绍几个重要术语:
1. 完全图:任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2条边。
2. 路径:对于从顶点Vi到Vj的一条路径,是指由所经过顶点组成的连续数列。
3. 简单路径:如果路径最终回到起始点则称为环,当中不重复叫简单路径。
4. 路径长度:路径上包含边的总数。
5. 相邻:如果Vi和Vj是E(G)中的一条边。
6. 关联:如果Vi和Vj相邻,则(VI,Vj)关联与Vi和Vj。
7. 连通分支:相连在一起的最大分支。
8. 度数:一个顶点拥有边的总数。
(2)有向图
若从顶点Vi到Vj的边有方向,则称这条边为有向边,也称为弧。用有序偶(Vi,Vj)来表示,Vj称为弧尾,Vj称为弧头。如果图中任意两个顶点之间的边都是有向边,则称该图为有向图。接下来介绍几个重要术语:
1. 完全图:任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边。
2. 强联通:从Vi到Vj和从Vj到Vi都存在路径,则称G是强连通图。
3. 强联通分支:有向图中的极大强连通子图称作有向图的强连通分支。
4. 出度数:以v为尾的弧的数目称为v的出度数。
5. 入度数:以顶点V为头的弧的数目称为v的入度数。
二、图的数据表示
1、邻接矩阵法
邻接矩阵存储使用二维数组存储图的信息:两个顶点相邻则表示为1,否则表示为0:
(1)二维数组中的对角线为0,表示不存在顶点到自身的边。
(2)要知道某个点的出度,就是顶点Vi在第i行的元素之和,入度就是该顶点所在列的元素之和。
(3)顶点Vi的所有邻接点就是把矩阵中第i行元素扫描一遍。

(4)对于有权值的网,二维数组中的元素不再是0,1表示是否存在边,而是把元素值表示为权值。不存在的边,权值记录为∞;对角线上的权值为0。

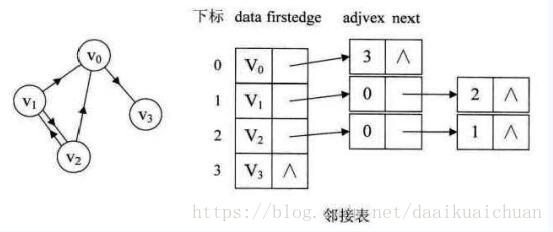
2、邻接表法
邻接矩阵对于顶点多而边数少的稀疏图造成存储空间的大量浪费。正如线性表的预先分配可能造成存储空间浪费,因此引入链式存储结构。同样可以考虑用链表存储边或弧。邻接表法表示了出度,但是查找入度就需要遍历整个图。
(1)图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过数组可以较容易地读取顶点信息,更加方便。另外,对于顶点数组中,每个数据元素还需要存储指向第一个邻接点的指针,以便于查找该顶点的边信息。
(2)图中每个顶点Vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以用单链表存储,无向图称为顶点Vi的边表,有向图则称为顶点Vi作为弧尾的出边表。
3、邻接矩阵法和邻接表法的demo:
#include
using namespace std;
struct Link
{
int val;
Link *next;
};
//邻接矩阵表示法
void Adjacency_Matrix(int data[][2])//传参的时候要指定第二个维度
{
int a[4][4] = { 0 };
for (int i = 0; i < 10; ++i)
{
a[data[i][0] - 1][data[i][1] - 1] = 1;//起点和终点间连一条边
}
for (int i = 0; i < 4; ++i)
{
for (int j = 0; j < 4; ++j)
cout << a[i][j] << " ";
cout << endl;
}
}
//邻接表表示法
void Adjacency_Map(int data[][2])
{
Link vec[4];
Link *newnode, *ptr;
for (int i = 0; i < 4; ++i)
{
vec[i].val = i + 1;
cout << vec[i].val << " : ";//把顶点值打印出来
vec[i].next = nullptr;
ptr = &vec[i];//暂存节点ptr
for (int j = 0; j < 10; ++j)
{
if (data[j][0] - 1 == i)//如果节点值=i,加入节点到链表头
{
newnode = new Link;
newnode->val = data[j][1] - 1;
//插入节点(相当于创建链表)
newnode->next = ptr->next;
ptr->next = newnode;
cout << newnode->val+1 << " ";
}
}
cout << endl;
}
}
//邻接表,使用标准库list
void Adjacency_Map2(int data[][2])
{
Link *newnode;
vector<list<Link*>> vec;
for (int i = 0; i < 4; ++i)
{
list<Link*> lst;
for (int j = 0; j < 10; ++j)
{
if (data[j][0] - 1 == i)//如果节点值=i,加入节点到链表头
{
newnode = new Link;
newnode->val = data[j][1] - 1;
newnode->next = nullptr;
lst.push_back(newnode);
}
}
vec.push_back(lst);
for (auto l : lst)
cout << l->val+1 << " ";
cout << endl;
}
}
int main(int argc, char const *argv[])
{
//图形各边的起点值和终点值(七桥问题)
int data[10][2] =
{
{ 1, 2 },{ 1, 3 },{ 1, 4 },{ 2, 1 },{ 2, 4 },
{ 3, 1 },{ 3, 4 },{ 4, 1 },{ 4, 2 },{ 4, 3 }
};
Adjacency_Matrix(data);
cout << endl;
Adjacency_Map(data);
cout << endl;
Adjacency_Map2(data);
return 0;
}
参考:https://www.cnblogs.com/weixuqin/p/6935290.html
https://www.cnblogs.com/moonlord/p/5938061.html