scipy库
from scipy import *
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import jn, yn, jn_zeros, yn_zeros
from scipy.integrate import quad, dblquad, tplquad
from numpy.fft import fftfreq
from scipy.fftpack import *
from scipy.linalg import *
from scipy import optimize
from scipy.interpolate import *
from scipy import stats
# 特殊函数
# scipy.special 包含了大量的贝塞尔函数# scipy
# 我们使用函数jn 和 yn, 它们是第一类和第二类实值贝塞尔函数
# jn_zeros 和 yn_zeros 代表了jn 和 yn 函数的零点
x = linspace(0, 10, 100)
fig, ax = plt.subplots()
for n in range(4):
ax.plot(x, jn(n, x), label=r"$J_%d(x)$" % n)
ax.legend()
# 积分
# 对f(x)从a到b的积分叫做数值积分，也叫简单积分。SciPy提供了一系列计算不同数值积分的函数，
# 包括quad,dblquad和tplquad，分别包含二重和三重积分。
# 对于简单函数而言，对于被积函数，我们可以用λ函数（无名称的函数）来代替清晰定义的函数：
val, abserr = quad(lambda x: exp(-x ** 2), -Inf, Inf)
print("numerical =", val, abserr)
def integrand(x, y):
return exp(-x**2-y**2)
x_lower = 0
x_upper = 10
y_lower = 0
y_upper = 10
# 注意，我们需要用λ函数对于y积分的极限，因为它们可以看做是x的函数。
val, abserr = dblquad(integrand, x_lower, x_upper, lambda x : y_lower, lambda x: y_upper)
print(val, abserr)
# 线性代数
# 线性代数部分包含了许多矩阵函数，包括线性方程的解，特征值的解，矩阵函数（例如矩阵指数函数），
# 许多不同的分解（SVD，LU，cholesky）等等。
A = array([[1,2,8], [3,7,6], [2,5,3]])
b = array([1,2,3])
x = solve(A, b)
print(x)
# 用eig计算特征值和特征向量
evals, evecs = eig(A)
print(evals)
print(evecs)
print(inv(A))
# 最优化
# 最优化问题（寻找函数的最大值或者最小值）是数学的一大领域，复杂函数的最优化问题，
# 或者多变量的最优化问题可能会非常复杂。
x = linspace(-5, 3, 100)
def f(x):
return 4*x**3 + (x-2)**2 + x**4
# 局部最小值
x_min_local = optimize.fmin_bfgs(f, 2)
print(x_min_local)
# 全局最小值
x_max_global = optimize.fminbound(f, -10, 10)
print(x_max_global)
# 插值
# 插值在SciPy中能够很容易和方便的实现：interpid函数，当描述X和Y的数据时，
# 返回值是被称之为x的任意值（X的范围）的函数，同时返回相应的插值y。
def f(x):
return sin(x)
n = arange(0, 10)
x = linspace(0, 9, 100)
y_meas = f(n) + 0.1 * randn(len(n)) # 噪声模拟测量
y_real = f(x)
# 线性插值
linear_interpolation = interp1d(n, y_meas)
y_interp1 = linear_interpolation(x)
# 三次样条差值
cubic_interpolation = interp1d(n, y_meas, kind='cubic')
y_interp2 = cubic_interpolation(x)
fig, ax = plt.subplots(figsize=(10,4))
ax.plot(n, y_meas, 'bs', label='noisy data')
ax.plot(x, y_real, 'k', lw=2, label='true function')
ax.plot(x, y_interp1, 'r', label='linear interp')
ax.plot(x, y_interp2, 'g', label='cubic interp')
ax.legend(loc=3);
# 统计
# scipy.stats包含了许多统计分布，统计函数和检验。
# 创建一个（离散）符合泊松分布的随机变量
X = stats.poisson(3.5) # 对于n = 3.5光子相干态的光子数分布
n = arange(0,15)
fig, axes = plt.subplots(3, 1, sharex=True)
# 绘制概率质量函数 (PMF)
axes[0].step(n, X.pmf(n))
# 绘制累计分布函数 (CDF)
axes[1].step(n, X.cdf(n))
# 绘制随机变量 X 的1000次随机实现的直方图
axes[2].hist(X.rvs(size=1000));
# 创建一个符合（连续）正态分布的随机变量
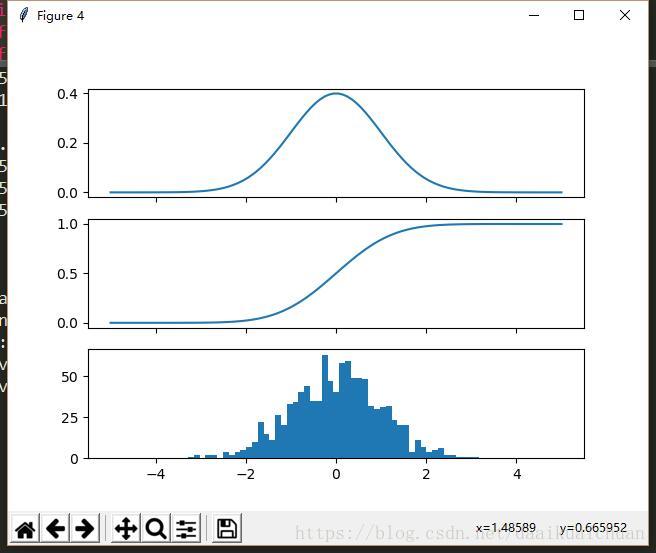
Y = stats.norm()
x = linspace(-5,5,100)
fig, axes = plt.subplots(3,1, sharex=True)
# 绘制概率分布函数 (PDF)
axes[0].plot(x, Y.pdf(x))
# 绘制累计分布函数 (CDF)
axes[1].plot(x, Y.cdf(x));
# 绘制随机变量 Y 的1000次随机实现的直方图
axes[2].hist(Y.rvs(size=1000), bins=50);
plt.show()
# 统计检验
# 检验两组（独立）随机数据是否来自同一个分布：
t_statistic, p_value = stats.ttest_ind(X.rvs(size=1000), X.rvs(size=1000))
print("t-statistic =", t_statistic)
print("p-value =", p_value) # 因为p值很大，我们不能拒绝原假设（两组随机数据有相同的均值）
