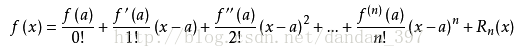详解Harris角点检测及代码实现
1. 首先,我们不禁要问什么是harris角点?
对于角点,到目前为止还没有明确的数学定义。但是你可以认为角点就是极值点,即在某方面属性特别突出的点。一般的角点检测都是对有具体定义的、或者是能够具体检测出来的兴趣点的检测。这意味着兴趣点可以是角点,是在某些属性上强度最大或者最小的孤立点、线段的终点,或者是曲线上局部曲率最大的点。
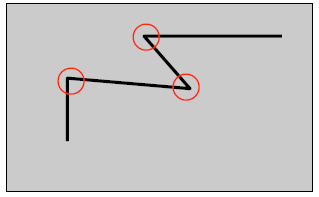
通俗的来说,在一副图像中,我们可以认为角点是物体轮廓线的连接点(见图1),当拍摄视角变化的时候,这些特征点仍能很好地保持稳定的属性。
图1 corner
角点在保留图像图形重要特征的同时,可以有效地减少信息的数据量,使其信息的含量很高,有效地提高了计算的速度,有利于图像的可靠匹配,使得实时处理成为可能。它的各种应用,这里我就不再赘述了。
2. 如何检测出harris角点?
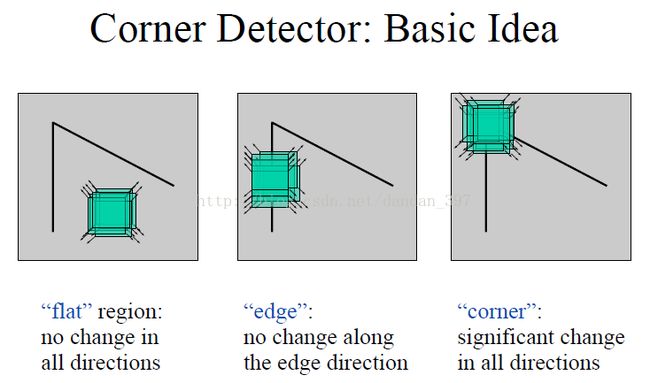
图2 角点检测的基本思想
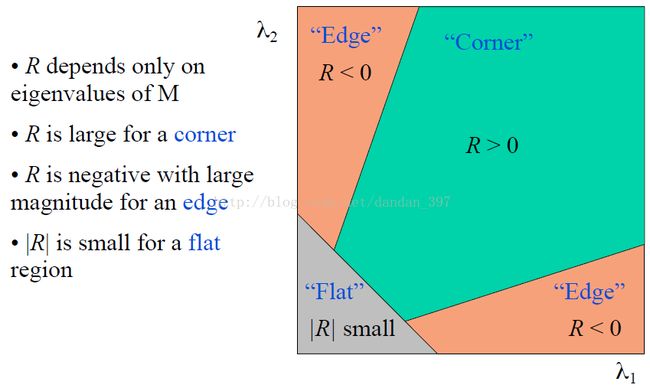
角点检测最原始的想法就是取某个像素的一个邻域窗口,当这个窗口在各个方向上进行小范围移动时,观察窗口内平均的像素灰度值的变化(即,E(u,v),Window-averaged change of intensity)。从上图可知,我们可以将一幅图像大致分为三个区域(‘flat’,‘edge’,‘corner’),这三个区域变化是不一样的。
其中,u,v是窗口在水平,竖直方向的偏移,
这里可以先简单复习一下泰勒级数展开的知识,因为马上就用到啦,
这是一维的情况,对于多元函数,也有类似的泰勒公式。
对I(x+u,y+v)进行二维泰勒级数展开,我们取一阶近似,有
图中蓝线圈出的部分我们称之为结构张量(structure tensor),用M表示。
讲到这里,先明确一点,我们的目的是什么?我们的目的是寻找这样的像素点,它使得我们的u,v无论怎样取值,E(u,v)都是变化比较大的,这个像素点就是我们要找的角点。不难观察,上式近似处理后的E(u,v)是一个二次型,而由下述定理可知,
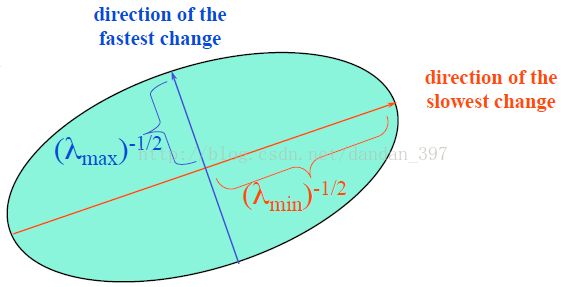
令E(u,v)=常数,我们可用一个椭圆来描绘这一函数。
椭圆的长短轴是与结构张量M的两个特征值![]() 相对应的量。通过判断
相对应的量。通过判断![]() 的情况我们就可以区分出‘flat’,‘edge’,‘corner’这三种区域,因为最直观的印象:
的情况我们就可以区分出‘flat’,‘edge’,‘corner’这三种区域,因为最直观的印象:
corner:在水平、竖直两个方向上变化均较大的点,即Ix、Iy都较大;
edge :仅在水平、或者仅在竖直方向有较大的点,即Ix和Iy只有其一较大 ;
flat : 在水平、竖直方向的变化量均较小的点,即Ix、Iy都较小;
而结构张量M是由Ix,Iy构成,它的特征值正好可以反映Ix,Iy的情况,下面我以一种更容易理解的方式来讲述椭圆的物理意义。
这样是不是更清楚了呢^_^......,因此我们可以得出结论:
当然,大牛们并没有止步于此,这样通过判断两个变量的值来判断角点毕竟不是很方便。于是他们想出了一种更好的方法,对,就是定义角点响应函数R(corner response function),
针对三种区域,R的取值如何呢?
至此,我们就可以通过判断R的值来判断某个点是不是角点了。
3. harris角点检测算法步骤
值得注意的是,在实际情况中,用来判断R的阈值依赖于实际图像的尺寸、纹理等因素,由于其不具有直观的物理意义,它的取值很难确定。通常我们采用间接的方法来判断R:通过选择图像中R值最大的前n个像素点作为特征点,再对提取到的特征点进行K*K邻域的非极大抑制处理就可以了。
4. Matlab 代码实现
clear;
% ori_im =double(imread('lena.jpg')); % 读取图像
ori_im = imread('pig.jpg');
% ori_im = imread('Baboon.bmp');
% figure,
% imshow(ori_im),
% title('the original image')
ori_gray = rgb2gray(ori_im);
% fx = [5 0 -5;8 0 -8;5 0 -5]; % 高斯函数一阶微分,x方向(用于改进的Harris角点提取算法)
fx = [-2 -1 0 1 2]; % x方向梯度算子(用于Harris角点提取算法)
Ix = filter2(fx,ori_gray); % x方向滤波
% fy = [5 8 5;0 0 0;-5 -8 -5]; % 高斯函数一阶微分,y方向(用于改进的Harris角点提取算法)
fy = [-2;-1;0;1;2]; % y方向梯度算子(用于Harris角点提取算法)
Iy = filter2(fy,ori_gray); % y方向滤波
Ix2 = Ix.^2;
Iy2 = Iy.^2;
Ixy = Ix.*Iy;
clear Ix;
clear Iy;
%% 考虑到图像一般情况下的噪声影响,采用高斯滤波去除噪声点
h= fspecial('gaussian',[7 7],2); % 产生7*7的高斯窗函数,sigma=2
Ix2 = filter2(h,Ix2);
Iy2 = filter2(h,Iy2);
Ixy = filter2(h,Ixy);
height = size(ori_gray,1);
width = size(ori_gray,2);
result = zeros(height,width); % 纪录角点位置,角点处值为1
%% 计算角点的响应函数R(即用一个值来衡量这个点是否是角点),并标记角点(R(i,j)>0.01*Rmax,且R(i,j)为3x3邻域局部最大值)
k=1;
lambda=zeros(height*width,2);
R = zeros(height,width);
for i = 1:height
for j = 1:width
M = [Ix2(i,j) Ixy(i,j);Ixy(i,j) Iy2(i,j)]; % auto correlation matrix
K = det(M); %求行列式
H = trace(M); %求迹
% R(i,j) = det(M)-0.06*(trace(M))^2;
R(i,j) = K-0.06*H^2;
lambda(k,:)=[K H];
k=k+1;
end;
end;
figure,
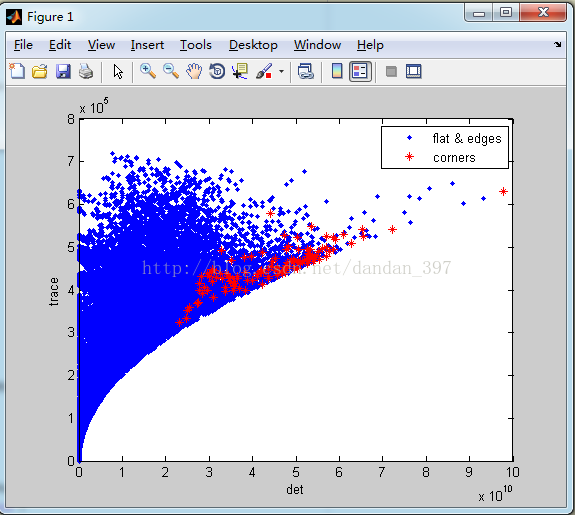
plot(lambda(:,1),lambda(:,2),'.');
ylabel('trace');xlabel('det');
%%
cnt = 0;
for i = 2:height-1
for j = 2:width-1
% 进行非极大抑制,窗口大小3*3
if R(i,j) > R(i-1,j-1) && R(i,j) > R(i-1,j) && R(i,j) > R(i-1,j+1) && R(i,j) > R(i,j-1) && R(i,j) > R(i,j+1) && R(i,j) > R(i+1,j-1) && R(i,j) > R(i+1,j) && R(i,j) > R(i+1,j+1)
result(i,j) = 1;
cnt = cnt+1;
end;
end;
end;
Rsort=zeros(cnt,1);
[posr, posc] = find(result == 1);
for i=1:cnt
Rsort(i)=R(posr(i),posc(i));
end;
[Rsort,ix]=sort(Rsort,1);
Rsort=flipud(Rsort);
ix=flipud(ix);
ps=120;
posr2=zeros(ps,1);
posc2=zeros(ps,1);
pos=zeros(ps,1);
for i=1:ps
posr2(i)=posr(ix(i));
posc2(i)=posc(ix(i));
pos(i)= (posr2(i)-1)*width+posc2(i);
end;
hold on,
plot(lambda(pos,1),lambda(pos,2),'r*');
legend('flat & edges','corners')
figure,
imshow(ori_im);
hold on;
plot(posc2,posr2,'g.');
实验结果:
再附一张中间结果图,det(M) 与trace(M)的分布图,便于大家更好地理解R,
我在上面做了一些标记,
欢迎大家一起学习交流!
C.Harris, M.Stephens. “A Combined Corner and Edge Detector”. 1988