关于八皇后问题的解法

八皇后问题是十九世纪著名的数学家高斯1850年提出：在8X8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

 

八皇后问题不是只用于这个有点无聊的数学问题上，不然就没什么研究意义了。在景观设计，道路布局，城市规划等方面有应用价值。比如布置景观时，要让N个景观互相不遮挡视线。

 

方案一  暴力法

最容易实现的，8层循环嵌套

当然OK，但它的复杂度惊人，O(nⁿ)，n为行列数

为了减少循环次数，针对该问题，最外层循环从第一列开始，向内层依次加1，最内层循环就从第八列开始了。

 

 

方案二  回溯法

八皇后问题是回溯法经典的例子

回溯法基本的思想是采用递归，并且分步解决问题

 

首先摆第一行的皇后（都是从第一列开始摆）

然后摆第二行的皇后，摆在第一列，发现不行；摆第二列，也不行；摆第三列，行了。

接下来再摆第三行，都是从第一列开始摆，如果不行就依次往后挪。

以此类推，对于某一行，如果这一行每列都不行，那么就得退回到上一行，（说明上一行的位置就已经不对了），上一行的皇后得往后再挪一格，如果已经是最后一格了，那就再退到上上一行……

如果摆到了最后一行，并且出现了一个解，那么将这个解输出后，同样再退回到上一行，将上一行的皇后往后挪一格……看看还有没有其他解，直到不可能再出现其他解为止。

 

棋盘信息，为了减少每次棋子调整带来的cost，我们可以用四个一维数组来表示。（传统上用一个二维数组表示的话，每次棋子调整要改变数组中很多个元素的值，而且相当混乱）

 

因为每个皇后的控制范围为一行、一列再加对角线，所以与之对应的，我们把棋盘分成8行、8列、15个左下斜对角线和15个右下斜对角线，每一项都用一个一维数组表示。每次摆一个皇后的时候，只需改变将与之对应的行、列、左下斜对角线和右下斜对角线数组中元素（说明此行、列、对角线上不能再放其他皇后了），也就是只需改变4个元素，而且这4个元素的在它们的数组中的下标与该皇后的横纵坐标有关（具体可以自己推算一下）。

 

类声明如下（cpp）

class ChessBoard

{

public:

         ChessBoard();

         ChessBoard(int);

         void findSolutions();

private:

         const bool available;  //表示行、列或对角线是否可用

         const int squares, norm;  //squares为行数，norm为squares-1（用于推算对角线的下标）

         bool *column, *leftDiagonal, *rightDiagonal;

         int *positionInRow;  //记录每一行皇后的下标（列号）

int howMany;  //已放好的皇后的个数

         void putQueen(int);

         void printBoard(ostream&);

         void initializeBoard();

};

 

关键方法的实现

void ChessBoard::putQueen(int row)

{

         int col;

         //对于每一行，都从第一格开始尝试摆

         for(col=0; col

         {

if(column[col]==available && leftDiagonal[row+col]==available && rightDiagonal[row-col+norm]==available)  //该格子可用

                   {

                            positionInRow[row]=col;

                            column[col]=!available;

                            leftDiagonal[row+col]=!available;

                            rightDiagonal[row-col+norm]=!available;

                  

                            if(row

                                     putQueen(row+1);  //进入下一行

                            else

                                     printBoard(cout);  //已找到一种解

                           

                            //由于下一行无法满足条件或者已找到一种解而退回来时

//恢复原来的状态，continue

column[col]=available;

                            leftDiagonal[row+col]=available;

                            rightDiagonal[row-col+norm]=available;

                   }

         }

}

 

其实用回溯法的话，也穷尽了每一种情况，也是exhaustive search，而且它的效率还不如暴力法，因为用了递归。

 

 

方案三 Best-First Search

由于我们最初的问题是求所有的摆法，所以不管怎样它一定是一个exhaustive search问题了。如果我们把问题改一下，对任意一种棋盘状态（八行里每行都只有一个皇后），怎样才能最快的调整为一个满足条件的状态。那这样的话，就不能再像之前那样盲目的去搜索了，得采用一定的策略了，就是Informed Search。Best-First Search、A*、Hill Climbing和Tabu Search等都能很好的解决该问题，我们以最基础的Best-First Search来讲述。

 

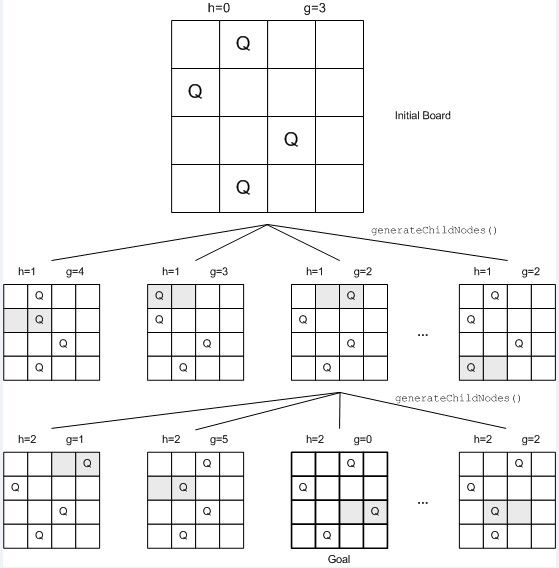
为了简化问题，我们先来看一个4X4的棋盘。

 

 

 

给定一个初始状态，我们每次都对它挪动一个棋子（也就是扩展后继节点）。第一张图中，第一行的棋子能朝左或右挪一格，第二行只能朝右挪一格，第三行第四行都能朝左或右挪一格。图中h表示深度，也就是调整的次数；g表示当前的Conflicts数，就是不符合的行、列和对角线总数。（图中可能h和g画反了，真正的h应该代表当前节点离目标节点的cost，也就是图中的g；真正的g应该代表初始节点到当前节点的cost，也就是图中的h）

根据Best-First Search算法，每次都将当前最好节点的所有后继节点都插入OPEN List中，每次都选择OPEN list中最好的节点进行扩展，直到选出的节点即为目标节点（图中的g=0）。每次都沿着当前最好的节点延伸，很快就能找到目标节点。