小波降噪详解

“小波”就是小的波形。所谓“小”是指它具有衰减性，而称之为“波”则是指它的波动性，其振幅正负相间的震荡形式。

小波在整个时间范围的幅度平均值是0，具有有限的持续时间和突变的频率和振幅，可以是不规则，也可以是不对称。

小波变换是时间（空间）频率的局部化分析，它通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。

傅里叶变换不具有局部性，而小波变换不但具有局部性，而且尺度参数a可以改变频谱结构和窗口的形状，起到“变焦”的作用，因此小波分析可达到多分辨率分析的效果。

参考资料：
http://blog.csdn.net/jbb0523/article/details/42028587

小波公式

对于任意实数对(a,b)，其中参数a必须为非零实数，称如下形式的函数：

为由小波母函数ψ(x)生成的依赖于参数(a,b)的连续小波函数，简称小波。小波母函数ψ(x)只有在原点的附近才会有明显偏离水平轴的波动，在远离原点的地方函数值将迅速衰减为零。所以对于任意参数(a,b)，小波函数ψa,b(x)在x=b附近存在明显的波动，远离x=b的地方迅速衰减到零（因为b是时移量，母小波是以原点为中心，时移就以b为中心了，如果有尺度变换的话再考虑进去就可以了）。

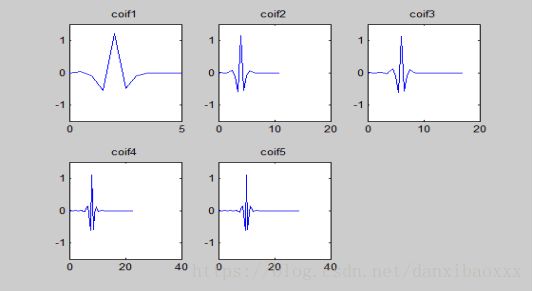
小波形状

db:

coif:

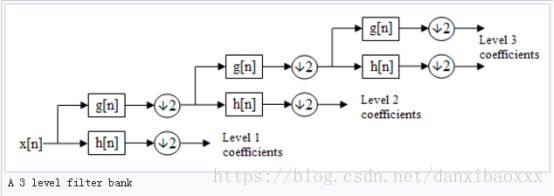
多尺度一维离散小波分解

the first step is

 

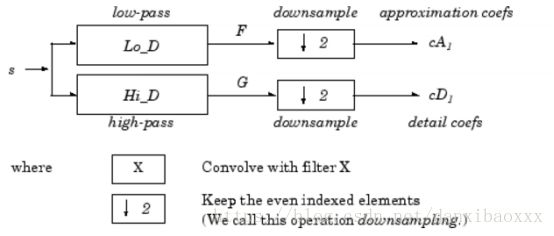
The length of each filter is equal to 2N. If n = length(s), the signals F and G are of length n + 2N −1 and the coefficients cA1 and cD1 are of length floor(n−12)+N.

The next step splits the approximation coefficients cA1 in two parts using the same scheme, replacing s by cA1, and producing cA2 andcD2, and so on.

The tree is known as a filter bank.

 

参考资料：
https://en.wikipedia.org/wiki/Discrete_wavelet_transform

 

小波去噪过程

去噪步骤
对原始信号进行小波分解，得到各细节分量（高频）与近似分量（低频）
对细节分量进行阈值处理
用处理后的各分量进行小波重构，得到去噪后的信号

去噪过程详解

依据MATLAB函数介绍整个去噪过程

函数原型

XD = wden(X,TPTR,SORH,SCAL,N,'wname')
[XD,CXD,LXD] = wden(...)

函数功能

wden is a one-dimensional de-noising function.
wden performs an automatic de-noising process of a one-dimensional signal using wavelets.
wden  returns a de-noised version XD of input signal X obtained by thresholding the wavelet coefficients.

参考资料
https://cn.mathworks.com/help/wavelet/ref/wden.html?searchHighlight=wden&s_tid=doc_srchtitle

1. 选择合适的小波，分解尺度

小波coif2，分解尺度N=4

2. 选择合适的计算阈值方法  

TPTR = 'rigrsure', adaptive threshold selection using principle of Stein's Unbiased Risk Estimate.
1)无偏似然估计原则(rigrsure): 是一种基于Stein无偏似然估计的自适应阈值选择。对于给定的阈值T，得到它的似然估计，再讲似然T最小化，就得到了所选的阈值，这是一种软件阈值估计。
TPTR = 'heursure', heuristic variant of the first option.
2)启发式阈值原则(heursure): 是无偏似然估计和固定阈值估计原则的折中。如果信噪比很小，按无偏似然估计原则处理的信号噪声较大，在这种情况下，就采用固定阈值形式。
TPTR = 'sqtwolog', threshold is sqrt(2*log(length(X))).
3)固定阈值原则(sqtwlolg): 固定阈值T的计算公式
TPTR = 'minimaxi', minimax thresholding.
4)极值阈值原则(minimax): 采用极大极小原理选择阈值，它产生一个最小均方误差的极值，而不是没有误差。统计学上，这种极值原理用来设计估计器。因为被消噪的信号可以看作与未知回归函数的估计器相似，这种极值估计器可在给定的函数中实现最大均方误差最小化。

参考资料
https://cn.mathworks.com/help/wavelet/ref/thselect.html

3. 阈值处理方法

SORH ('s' or 'h') is for soft or hard thresholding

 

 

 

硬阈值方法能够保留更多尖峰特征，软阈值方法使重建信号比较光滑。

参考资料
https://cn.mathworks.com/help/wavelet/ref/wthresh.html

4. 对细节信号做阈值处理

SCAL defines multiplicative threshold rescaling:
'one' for no rescaling
'sln' for rescaling using a single estimation of level noise based on first-level coefficients
'mln' for rescaling done using level-dependent estimation of level noise
Wnoisest returns estimates of the detail coefficients' standard deviation for levels
The estimator used is Median Absolute Deviation / 0.6745, well suited for zero mean Gaussian white noise in the de-noising one-dimensional model.

参考资料
https://cn.mathworks.com/help/wavelet/ref/wnoisest.html?searchHighlight=wnoisest&s_tid=doc_srchtitle