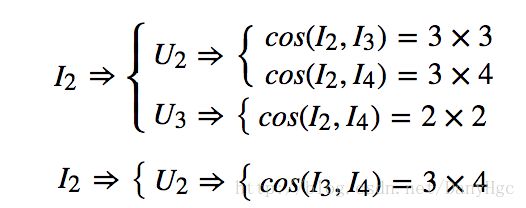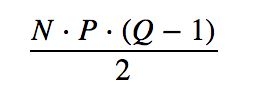举例讲解协同过滤中相似度的计算方式

协同过滤中相似度的计算很有技巧性，下面对比几种计算的方式。

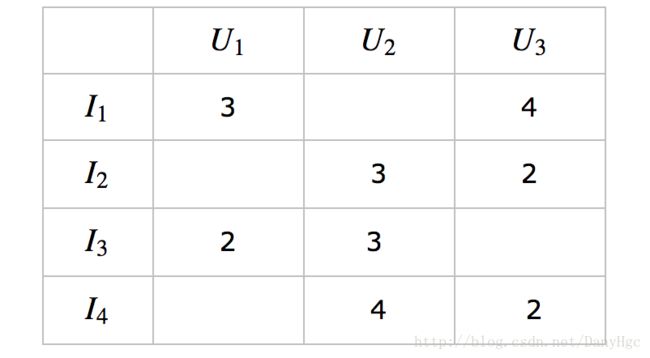
假设输入的Item-User矩阵为：

设用户共有M个，Item共有N个，在本例子中，M=3,N=4M=3,N=4。矩阵中为空的元素代表对应的用户对Item没有行为，也可以认为该用户对该Item的评分为0.

一、用二维数组依次计算

这种方式的实现步骤如下：

1、遍历User，依次取出U1,U2,U3U1,U2,U3。当取到U1U1的时候，计算所有item之间的相似度，此处以余弦方式度量相似度。因为相似度矩阵是一个对称矩阵，所以只计算上三角或者下三角即可。当计算U2U2的时候，需要累加U1U1的计算结果，U3U3同样要累加前面的计算结果，这样当user遍历完成之后，即可得到两个Item之间的内积，当然余弦相似度还要除以两个Item的模长的乘积。模长的计算可以在遍历User的时候同步计算。

计算内积的具体过程为：

2、用内积除以模长得到余弦相似度，这一步比较简单，不详细讨论。

现在来分析一下这种方法的时间复杂度。很明显要遍历User，上面已经假设User的数量为M，而对每一个User而言，要计算所有Item两两之间的相似度，因之需要计算相似度矩阵的上三角或下三角，所以其计算的次数为：

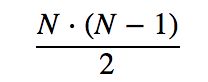
考虑所有的用户，还要在上面的基础上再乘以MM，所以最后的次数为：

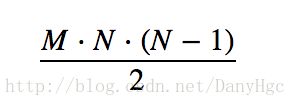
二、采用HashMap查找计算

这种方法只计算User-Item矩阵中值不为空的元素，对稀疏的矩阵而言，没有冗余的计算。但是需要额外构造一个ItemHashMap，从遍历ItemHashMap开始。

在ItemHashMap中，Item为key，User为value。

1、遍历ItemHashMap，依次取出I1,I2,I3,I4I1,I2,I3,I4。取到I1I1的时候，先从ItemHashMap中查找看过该Item的User有哪些，在本例子中为U1,U3U1,U3。然后再分别计算这些User中每个User看过的Item之间的相似度，这一步很重要，是为了避免计算User-Item矩阵中为空的元素。

2、用户U1U1看过的Item有I1,I3I1,I3，用户U3U3看过的Item有I1,I2,I4I1,I2,I4。那么作如下计算：

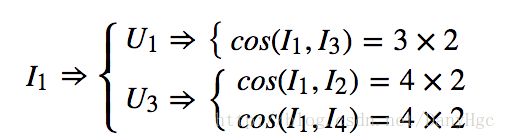
3、同理，可以这样计算I2,I3,I4I2,I3,I4。因为是对称矩阵，只需要计算相似度矩阵上三角或者下三角即可。如下所示：

假设平均每个Item被P个用户看过，平均每个用户看过Q个Item，那么应当有：

分析上面的过程，不难发现，这种方式的计算次数为：

在实际的数据中，User-Item矩阵必然是稀疏，如果User-Item矩阵一点都不稀疏，也即没有不为空的元素，那么也就失去了推荐的意义，因为对于每一个用户而言，他把所有的Item都看过了，那还给他推荐什么呢？正常情况下，应该有P≪MP≪M，所以这种算法是有意义的。

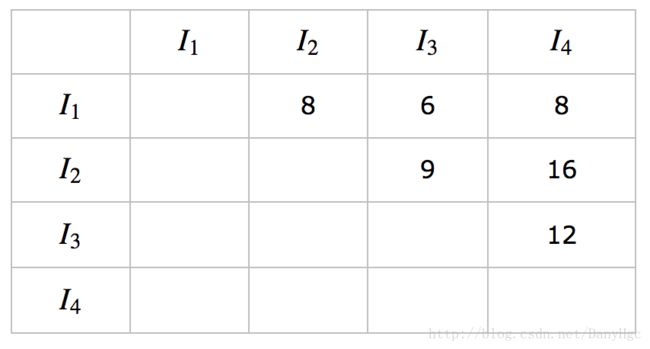
上面两种方法计算的相似度矩阵是一致的，如下所示：

三、只使用UserHashMap实现

这种方式在实现第二种方式达到的效果之外，还可以节省空间。大概的思想是，遍历UserHashMap，每取到一个User之后，先获取该User所看过的Item，然后计算这些看过的Item两两之间的相似度，然后将结果保存在相似度矩阵中，后面的User生成的相似度直接累加上去即可，这样最终的结果也就生成了。

更多文章参考https://www.cnblogs.com/lengyue365/p/5279435.html