线性回归

线性回归（Linear Regression）

标签 : 监督学习

@author : [email protected]
@time : 2016-06-19

对于一个的拥有 m 个观测的训练数据集 X 而言，回归的目的就是要对新的 n 维输入 x ，预测其对应的一个或者多个目标输出 t 。

线性回归模型的基本特性就是：模型是参数的线性函数。

最简单的线性回归模型当然是模型是参数的线性函数的同时，也是输入变量的线性函数，或者叫做线性组合。

如果我们想要获得更为强大的线性模型，可以通过使用一些输入向量 x 的基函数 f(x) 的线性组合来构建一个线性模型。这种模型，由于它是参数的线性函数，所以其数学分析相对较为简单，同时可以是输入变量的非线性函数。

从概率的角度来说，回归模型就是估计一个条件概率分布： p(t|x) 。因为这个分布可以反映出模型对每一个预测值 t 关于对应的 x 的不确定性。基于这个条件概率分布对输入 x 估计其对应的 t 的过程，就是最小化损失函数（loss function）的期望的过程。

对于线性模型而言，一般所选择的损失函数是平方损失。

由于模型是线性的，所以在模式识别和机器学习的实际应用中存在非常大的局限性，特别是当输入向量的维度特别高的时候，其局限性就更为明显。但同时，线性模型在数学分析上相对较为简单，进而成为了很多其他的复杂算法的基础。

一般线性回归

对于一个一般的线性模型而言，其目标就是要建立输入变量和输出变量之间的回归模型。该模型是既是参数的线性组合，同时也是输入变量的线性组合。从数学上来说，如果定义 y^ 为模型期望的输出，那么

y^(w,x)=w0+w1∗x1+w2∗x2+...+wn∗xn

这里，我们定义 ω={w0,w1,w2,...,wn} 为参数向量， 若取 x0=1 ，则输入向量 x={x0,x1,x2,...,xn} 是 n+1 维的。

在回归模型中，有一个比较特殊的回归模型： 逻辑回归(Logistic Regression)，这是一个用于分类的线性回归模型。

下面给出一份简单的线性回归的代码

#!/usr/bin/python
# -*- coding: utf-8 -*-

"""
author ： [email protected]
time : 2016-06-19-20-48

这个是线性回归的示例代码
使用一条直线对一个二维数据拟合

"""
print(__doc__)


import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model

# 加载用于回归模型的数据集
# 这个数据集中一共有442个样本，特征向量维度为10
# 特征向量每个变量为实数，变化范围（-.2 ，.2）
# 目标输出为实数，变化范围 （25 ，346）
diabetes = datasets.load_diabetes()

# 查看数据集的基本信息
print diabetes.data.shape
print diabetes.data.dtype
print diabetes.target.shape
print diabetes.target.dtype

# 为了便于画图显示
# 仅仅使用一维数据作为训练用的X
# 这里使用np.newaxis的目的是让行向量变成列向量
# 这样diabetes_X每一项都代表一个样本
diabetes_X = diabetes.data[:, np.newaxis, 2]

# 此时diabetes_X的shape是(442L, 1L)
# 如果上面一行代码是：diabetes_X = diabetes.data[:, 2]
# 则diabetes_X的shape是(442L，)，是一个行向量
print diabetes_X.shape

# 人工将输入数据划分为训练集和测试集
# 前400个样本作为训练用，后20个样本作为测试用
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]

# 初始化一个线性回归模型
regr = linear_model.LinearRegression()

# 基于训练数据，对线性回归模型进行训练
regr.fit(diabetes_X_train, diabetes_y_train)

# 模型的参数
print '模型参数：', regr.coef_
print '模型截距：', regr.intercept_

# 模型在测试集上的均方差（mean square error）
print("测试集上的均方差: %.2f"
      % np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# 模型在测试集上的得分，得分结果在0到1之间，数值越大，说明模型越好
print('模型得分: %.2f' % regr.score(diabetes_X_test, diabetes_y_test))

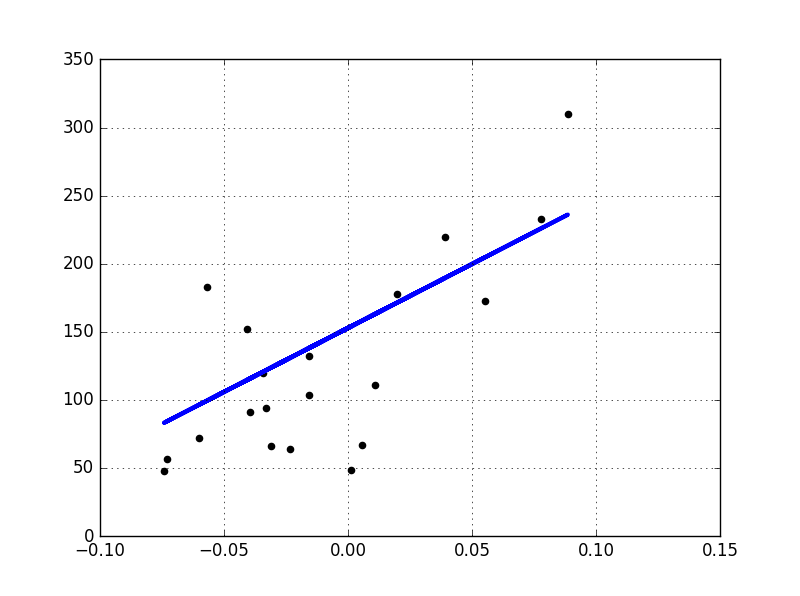
# 绘制模型在测试集上的效果
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test), color='blue',
         linewidth=3)

plt.grid()
plt.show()

最小二乘法（Ordinary Least Squares）

线性回归（Linear Regression）通过寻找合适的 ω={w0,w1,w2,...,wn} ，使得观测样本集合 X （这里观测样本集合 X 在很多的外文书籍中比如RPML，叫做设计矩阵（design matrix）），和目标输出 y 之间的残差平方和最小(residual sum of squares)，从数学上来说，其的目标问题或者叫做损失函数是：

J(w)=minw∥Xw−y∥2

最小乘法的证明

对于上面的损失函数而言， J(w) 显然是非负的，其去最小值的充要条件就是 ∥Xw−y∥2 的倒数为0时的 w 的取值，从矩阵的角度来写这个式子：

∥Xw−y∥2=(Xw−y)T(Xw−y)

容易得到其关于 w 的导数为：

XT(Xw−y)+XT(Xw−y)=0

即：

w=(XTX)−1XTy

这里，我们将 X+≡(XTX)−1XT 定义为X的伪逆矩阵。

这个是一个非常好的结果，它说明使用最小二乘法，从数学上是可以直接通过公式来求解出参数 w 的。

注意：最小二乘法对 ω 的估计，是基于模型中变量之间相互独立的基本假设的，即输入向量 x 中的任意两项 xi 和 xj 之间是相互独立的。如果输入矩阵 X 中存在线性相关或者近似线性相关的列，那么输入矩阵 X 就会变成或者近似变成奇异矩阵（singular matrix）。这是一种病态矩阵，矩阵中任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化。这将导致最小二乘法对观测数据的随机误差极为敏感，进而使得最后的线性模型产生非常大的方差，这个在数学上称为多重共线性（multicollinearity）。在实际数据中，变量之间的多重共线性是一个非常普遍的现象，其产生机理及相关解决方案在“特征选择和评估”中有介绍。

基于基函数的线性回归模型

前面已经提到过，线性回归模型的基本特征就是，模型是参数向量 ω={w0,w1,w2,...,wn} 的线性函数，上面的那个例子模型同时也是输入变量 x 的线性函数，这极大地限制了模型的适用性。这里使用基函数（basis function）对上面的线性模型进行拓展，即：线性回归模型是一组输入变量 x 的非线性基函数的线性组合，在数学上其形式如下：

y(x,w)=w0+∑j=1Mωjϕj(x)

这里 ϕj(x) 就是前面提到的基函数，总共的基函数的数目为 M 个，如果定义 ϕ0(x)=1 的话，那个上面的式子就可以简单的表示为：

y(x,w)=∑j=0Mωjϕj(x)=wTϕ(x)

w=(w0,w1,w2,...,wM)

ϕ=(ϕ0,ϕ1,ϕ2,...,ϕM)

在“特征选择和评估”中，实际拿到手的数据，由于各种原因，往往不能直接应用到机器学习算法中，需要对原始数据做一些预处理或者是特征提取的操作，而那些从原始输入向量 x 中提取出来的特征， 就是这一个个的 ϕj(x) .

通过使用非线性的基函数，我们可以使得线性模型 y(x,w) 成为输入向量 x 的非线性函数。

下面举一些基于不同基函数的线性模型 y(x,w) 的例子:

1. ϕj(x)=xj
   这里取 M=n ,那么就可以很容易的得到：
   

   y(x,w)=w0+∑j=1Mωjϕj(x)=w0+w1∗x1+w2∗x2+...+wn∗xn

2. ϕj(x)=xj
   这里就是典型的多项式曲线拟合（Polynomial Curve Fitting），其中 M 是输入变量 x 的最高次数，同时也是模型的复杂度。多项式曲线拟合的一个缺陷就是这个模型是一个输入变量的全局函数，这使得对输入空间的一个区间的改动会影响到其他的区间，这个问题可以通过将输入空间切分成不同的区域，对不同的区域各自在各自的区域中做曲线拟合来解决，这个方法就是经典的样条函数（spline function）。笔记中有专门的一节详细的论述了多项式曲线拟合相关的特性。
   

   y(x,w)=w0+∑j=1Mωjϕj(x)=∑j=0Mωjxj

3. ϕj(x)=exp{−(x−μj)22s2}
   这里 μj 表示的是该基函数在输入空间中的位置，参数 s 控制的是基函数的空间尺度，这个基函数往往会被称为高斯基函数（Gaussian basis function）。需要强调一点，这里的高斯函数并不是输入空间的概率分布，其并没有概率意义。由于每个基函数前面都有一个比例系数 ωj ，所以，对参数的归一化（coefficient normalization）并不是必需的。
   

   y(x,w)=w0+∑j=1Mωjϕj(x)=w0+∑j=1Mωjexp{−(x−μj)22s2}

4. ϕj(x)=σ(x−μjs)
   这个基函数叫做 sigmoid 函数，其定义为：
   

   σ(a)=11+exp(−a)
   
   与这个函数拥有相同效果的一个函数叫做 tach 函数，其定义为：
   
   tanh(a)=2σ(a)−1

   在神经网络中，这两个基函数有着非常广泛的应用。其实从根本上来讲，神经网络的每一层，也是一些基函数的线性组合，神经网络之所以能处理非线性问题，其根本也是由于采用了合适的非线性基函数。

y(x,w)=w0+∑j=1Mωjϕj(x)=w0+∑j=1Mωj11+exp(−a)

线性回归的在线学习算法

在《多项式回归》中，介绍了线性模型的极大似然估计解释：对于训练数据 {X,t} 而言，可以使用极大似然估计来计算参数 w 和 σ2 ，其中 w 是 y(xn,w) 的参数；而 σ2 是噪声的方差：

p(t|X,w,σ2)=∏n=1NN(tn|y(xn,w),σ2)

像OLS算法这种，一次性就将训练数据集中的 N 个数据全部都用于 p(t|X,w,σ2) 的估计中，然后通过求导得到参数的估计结果。这种算法的模型，称为批处理技术（Batch techniques），在Andrew Ng的机器学习课程视频中，对这个有说明。其主要缺点就在于，面对大的数据集的时候，其计算成本会非常的大。

当数据集特别大的时候，这种批处理技术就不再适用，就有一种称为序列学习算法（Sequential learning），也叫作在线算法（on-line algorithms）的算法得到了广泛的应用。

说得简单一点，序列学习算法就是将数据的样本点，看成在时间上有序的，即，数据集合不是一次性得到全部的数据，而是一个样本一个样本采集得到的。那么，在训练算法的时候，也就可以一个样本一个样本的输入的训练算法的中，利用新的样本不断的改进模型，进而达到学习的目的。

梯度下降法

有前面可以知道，线性回归的损失函数为:

J(w)=minw∥Xw−y∥2

其关于参数 w 梯度为：

∇J(w)=2XT(Xw−y)

梯度下降法就是：

wk=wk−1−ρk∇J(w)

通过迭代，求得 wk

随机梯度下降法

随机梯度下降法，就是这里要说的在线学习算法，它不像上面的梯度下降法，每次迭代都使用了全部的数据集，这里每次迭代仅仅使用一个样本：

wk=wk−1−ρkxk(xTkwk−1−yk)

这里需要说明的是， ρk 必须满足两个条件：

∑k=1∞ρk→∞∑k=1∞ρ2k<∞

这个过程，其实是根据新的输入样本，对 wk 的一个不断的修正的过程，一般来说，我们会把 ρk 后面的式子称为修正量。

折两个条件，保证了在迭代过程中估计的修正值，会趋近于零。因此，对于足够大的 k 而言，迭代会突然停止，但是，由于有第一个条件的存在，这个停止不会发生的太早，并且不会再离结果非常远的时候，就停止了迭代。上面的第二个条件保证了，对于变量的随机性噪声，噪声的累积保持有限。