流行排序和佩奇排序简述（manifold rank & Page rank）

流行排序和佩奇排序简述（manifold rank & Page rank）

最近看了一篇文章，其中用到了流行排序（manifold ranking），于是就重新补查了一下流行排序，又因为流行排序中的收敛性用到了佩奇排序（page rank），所以这里就简单的叙述一下page rank和manifold rank。希望大家能有所收获。由于manifold rank中用到了page rank的思想，因此此博客就先叙述page rank，再进而叙述manifold rank。

佩奇排序（Page rank）

佩奇排序因其英文名字是page rank，并且最早应用于搜索网页的排序，所以佩奇排序也被叫做页排序。

实际上Page rank之所以得名是因为google创始人之一的拉里佩奇（Lawrence Page）有关，他也是page rank的提出者，这一算法被用于解决网页排序的问题。如下图所示，我们使用不同的搜索引擎，往往会得到不同的结果。那么google最初是如何实现网页的排序的呢？那就是page rank啦。

page rank的基本思想是利用马尔科夫过程中的马尔科夫稳定性（markoff stability），其算法步骤也是十分的简单：

（1）假设我们正在上网，我们会随便的选一个网页待上一会儿，然后再随机的跳转到该网页连接的另外的网页，通过上述的方式，我们就能得到状态转移矩阵。

（2）然后一直重复上次操作，直到收敛（其收敛是由于马尔科夫的稳定性）。

（3）最后通过比较上网者浏览所有网页的概率分布，对网页进行排序。概率越大的网页，排序越靠前。

--》--》

如上图所述，首先作为一个随机的上网者，我们访问ABCD四个网站的概率都是1/4，网站A有分别以1/3的概率跳转到BCD，以此类推，我们就可以得到状态状态转移矩阵M，其中第1列就表示网站A跳转到BCD的概率，又因为先假设A不能够自己跳转到自己所以A到A的跳转概率是0。因此经过一次跳转的结果便是V1,以此类推，我们继续用M*V1便可以得到第二部跳转的状态转移矩阵。我们就这样一直在网页间进行跳转，由于马尔科夫的稳定性，我们知道这样的跳转最终会导致收敛，最后的用户浏览A,B,C,D的概率分布就为3/9,2/9,2/9,2/9，最后我们按照这个概率分布的大小对网页进行排序，这就是page rank啦！

但是这个原始的page ranking是存在bug的，也就是会有一些先验假设:如，1.不能存在某个网页不跳转到任何的网页，也就是上面的terminal point的问题，这会使得最后A,B,C,D的概率分布都为0。2.也不能存在某个网页自己跳转到自己，也就是上面的 trap problem的问题，这会使得A,B,C,D的概率在有自己跳转的网页上的概率为1，而其他的概率为0。

有没有什么方法解决这一问题呢？答案是肯定的。

那就是在状态转移方程中加入扰动项，即红框中的内容。这样我们就能使浏览者以一定的概率跳出terminal point和trap problem的问题使得状态转移能够收敛。

流行排序（Manifold ranking）

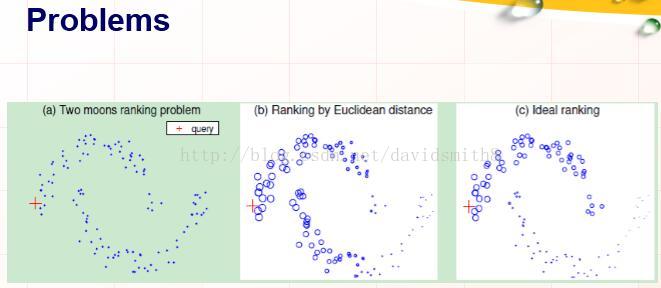
流行排序出处是Dengyong Zhou的“Ranking on Data Manifolds” NIPS(2003)，其要解决的问题是如何实现如下数据的排序：

其中红色十字被称为是问询点（query），我们想通过问询问询点实现对数据的排序，使得数据的排序像(c)图中展现的那样，如果我们只是单纯的使用欧氏距离对这些数据点进行排序则会得到图(b)所示的结果，但是我们希望得到的排序是像图(c)一样的排序。这时我们该如何处理呢？

Dengyong Zhou的做法是：

（1）先衡量数据点和问询点之间，以及这些数据点之间的距离，并将这些点两两之间的距离按照升序进行排列，同时将这两点进行连接，重复实现这两点之间的连接直到生成一个连接图。（连接图在下面的图中会有所展示）。

（2）根据生成的连接图和边的长度（两点之间的距离）设置边的权重，权重的公式是采用的e指数的形式，如上图2步所示。如果没有连接，即没有边，则权重为零。这样我们就得到了一个权重矩阵W。

（3）用一个对角矩阵D对W进行归一化处理，D的对角线上的元素是W中所对应的行的元素的加和。

（4）与前面将的改进的page ranking相似，令“浏览者”在这个图上进行随机浏览，也可称之为迭代传播，直至收敛。

（5）最后使用收敛后的排序值的大小f*最为最后排序的依据。

可赞的是，作者还给出了收敛性的证明，以及收敛的值。

如上图3中的结果就是最后收敛的值，但是最后作者还给出了建议，由于直接计算最后收敛的结果在数据很多的情况下是不可行的，所以还是建议大家使用迭代的方式进行计算。

最后给出流行排序的迭代步骤和结果图。

如上图1中所示的就是，所生成的连接图。

关于流行排序我就写到这里了，仅为了记录一下我看过的东西，备忘一下，也希望能够对大家有所帮助。