【机器学习】交叉验证、正则化实例Python代码实现

前言

机器学习常用的数据集网址：数据集
运行环境：python3.6（这里我用的anaconda的jupyter notebook）

1. 对比不同模型的交叉验证的结果

数据集来源：红酒数据集

这份数据集包含来自3种不同起源的葡萄酒的共178条记录。13个属性是葡萄酒的13种化学成分。通过化学分析可以来推断葡萄酒的起源。值得一提的是所有属性变量都是连续变量。

from sklearn import datasets   # 用于调用sklearn自带的数据集

# 用load_wine方法导入数据
wine_data = datasets.load_wine()
print(wine_data.feature_names)  # 输出的就是13个属性名

data_input = wine_data.data  # 输入输出数据
data_output = wine_data.target

from sklearn.ensemble import RandomForestClassifier   # 随即森林模型
from sklearn.linear_model import LogisticRegression   # 逻辑回归模型
from sklearn import svm     # 支持向量机
from sklearn.model_selection import cross_val_score

# 模型重命名   
rf_class = RandomForestClassifier(n_estimators=10) 
log_class = LogisticRegression()
svm_class = svm.LinearSVC()

# 把数据分为四分，并计算每次交叉验证的结果，并返回
print(cross_val_score(rf_class, data_input, data_output, scoring='accuracy', cv = 4))

# 这里的cross_val_score将交叉验证的整个过程连接起来，不用再进行手动的分割数据
# cv参数用于规定将原始数据分成多少份
accuracy = cross_val_score(rf_class, data_input, data_output, scoring='accuracy', cv = 4).mean() * 100
print("Accuracy of Random Forests is: " , accuracy)

accuracy = cross_val_score(log_class, data_input, data_output, scoring='accuracy', cv = 4).mean() * 100
print("Accuracy of logistic is: " , accuracy)

accuracy = cross_val_score(svm_class, data_input, data_output, scoring='accuracy', cv = 4).mean() * 100
print("Accuracy of SVM is: " , accuracy)

2. 正则化（regularization）

数据准备

import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 10

x = np.array([1.4*i*np.pi/180 for i in range(0,300,4)])
np.random.seed(20)  #随机数
y = np.sin(x) + np.random.normal(0,0.2,len(x))  # 加噪音
data = pd.DataFrame(np.column_stack([x,y]),columns=['x','y'])
plt.plot(data['x'],data['y'],'.')

# 模型复杂度设置
for i in range(2,16):  
    colname = 'x_%d'%i      # 变量名变为 x_i形式
    data[colname] = data['x']**i
    print(data.head()) # 显示五行

LinearRegression(normalize=True) 加入正则化的线性回归

# 模型复杂度可变
from sklearn.linear_model import LinearRegression
def linear_regression(data, power, models_to_plot):
    # 初始化预测器
    predictors=['x']
    if power>=2:
        predictors.extend(['x_%d'%i for i in range(2,power+1)])

    # 模型训练
    linreg = LinearRegression(normalize=True)
    linreg.fit(data[predictors],data['y'])

    # 预测
    y_pred = linreg.predict(data[predictors])

    # 是否要画图（复杂度是否在models_to_plot中）为了便于比较选择性画图
    if power in models_to_plot:
        plt.subplot(models_to_plot[power])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for power: %d'%power)

    # 返回结果
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([linreg.intercept_])
    ret.extend(linreg.coef_)
    return ret

col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['model_pow_%d'%i for i in range(1,16)]
coef_matrix_simple = pd.DataFrame(index=ind, columns=col)

# 定义作图的位置与模型的复杂度
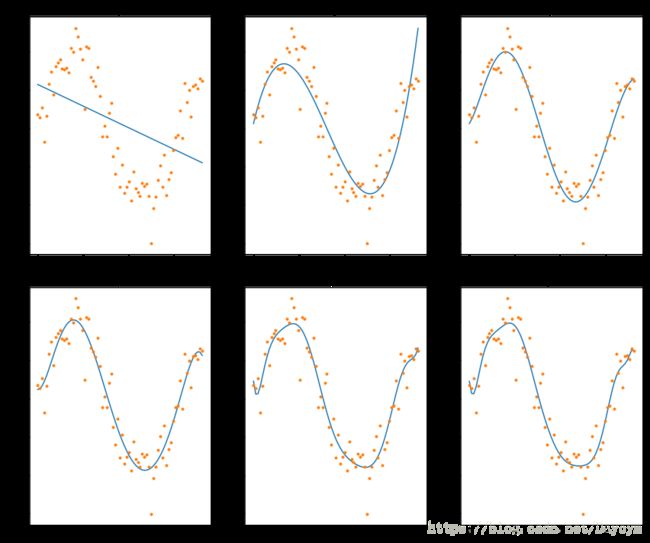
models_to_plot = {1:231,3:232,6:233,8:234,11:235,14:236}

# 画图
for i in range(1,16):
    coef_matrix_simple.iloc[i-1,0:i+2] = linear_regression(data, power=i, models_to_plot=models_to_plot)

Ridge（L2-norm）

from sklearn.linear_model import Ridge

def ridge_regression(data, predictors, alpha, models_to_plot={}):
    # 模型训练
    ridgereg = Ridge(alpha=alpha,normalize=True)
    ridgereg.fit(data[predictors],data['y'])

    # 预测
    y_pred = ridgereg.predict(data[predictors])

    # 选择alpha值画图
    if alpha in models_to_plot:
        plt.subplot(models_to_plot[alpha])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for alpha: %.3g'%alpha)

    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([ridgereg.intercept_])
    ret.extend(ridgereg.coef_)
    return ret


predictors=['x']
predictors.extend(['x_%d'%i for i in range(2,16)])

# 定义alpha值
alpha_ridge = [1e-15, 1e-10, 1e-8, 1e-4, 1e-3,1e-2, 1, 5, 10, 20]

col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['alpha_%.2g'%alpha_ridge[i] for i in range(0,10)]
coef_matrix_ridge = pd.DataFrame(index=ind, columns=col)

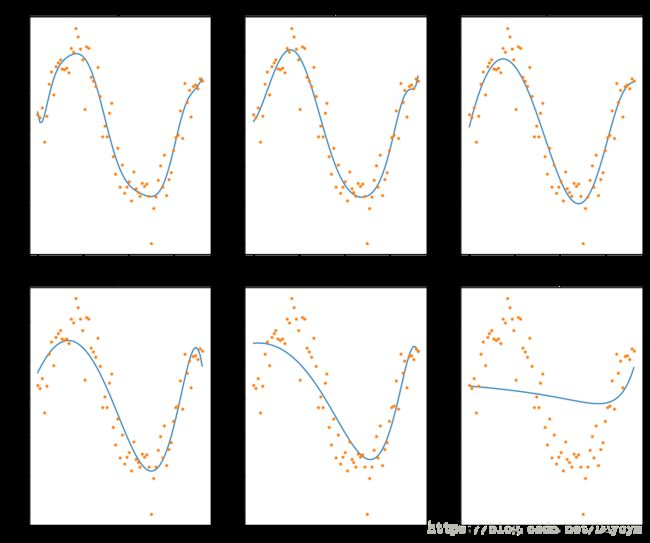
models_to_plot = {1e-15:231, 1e-10:232, 1e-4:233, 1e-3:234, 1e-2:235, 5:236}
for i in range(10):
    coef_matrix_ridge.iloc[i,] = ridge_regression(data, predictors, alpha_ridge[i], models_to_plot)

Lasso（L1-norm）

from sklearn.linear_model import Lasso
def lasso_regression(data, predictors, alpha, models_to_plot={}):
    #Fit the model
    lassoreg = Lasso(alpha=alpha,normalize=True, max_iter=1e5)
    lassoreg.fit(data[predictors],data['y'])
    y_pred = lassoreg.predict(data[predictors])

    #Check if a plot is to be made for the entered alpha
    if alpha in models_to_plot:
        plt.subplot(models_to_plot[alpha])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for alpha: %.3g'%alpha)

    #Return the result in pre-defined format
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([lassoreg.intercept_])
    ret.extend(lassoreg.coef_)
    return ret

predictors=['x']
predictors.extend(['x_%d'%i for i in range(2,16)])

# 定义alpha值去测试
alpha_lasso = [1e-15, 1e-10, 1e-8, 1e-5,1e-4, 1e-3,1e-2, 1, 5, 10]

col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,16)]
ind = ['alpha_%.2g'%alpha_lasso[i] for i in range(0,10)]
coef_matrix_lasso = pd.DataFrame(index=ind, columns=col)

# 定义画图的模式
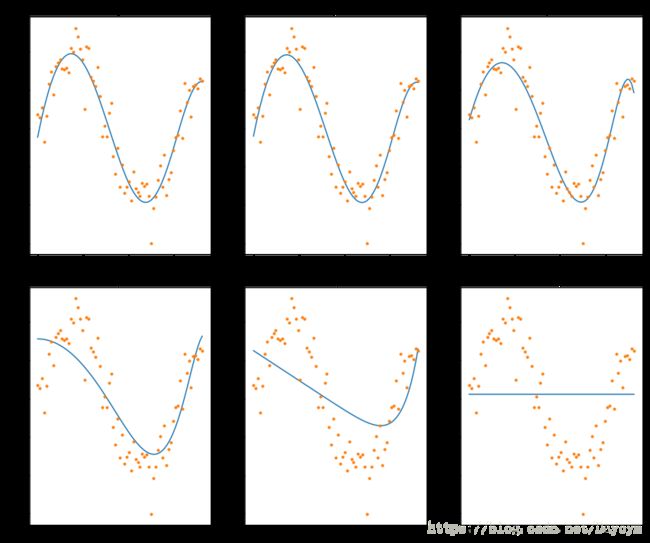
models_to_plot = {1e-10:231, 1e-5:232,1e-4:233, 1e-3:234, 1e-2:235, 1:236}

#迭代10个alpha值:
for i in range(10):
    coef_matrix_lasso.iloc[i,] = lasso_regression(data, predictors, alpha_lasso[i], models_to_plot)