数据结构第十二周项目--验证算法

/*  
*Copyright(c)2017,烟台大学计算机与控制工程学院  
*All rights reserved.  
*作    者：李哲  
*版 本 号：v1.0  
*问题描述：验证算法 
*/  

（1）Prim算法的验证

#include 
#include 
#include "graph.h"

void Prim(MGraph g,int v)
{
    int lowcost[MAXV];          //顶点i是否在U中
    int min;
    int closest[MAXV],i,j,k;
    for (i=0; i

（2）Kruskal算法的验证

#include 
#include 
#include "graph.h"
#define MaxSize 100
typedef struct
{
    int u;     //边的起始顶点
    int v;     //边的终止顶点
    int w;     //边的权值
} Edge;

void InsertSort(Edge E[],int n) //对E[0..n-1]按递增有序进行直接插入排序
{
    int i,j;
    Edge temp;
    for (i=1; i=0 && temp.w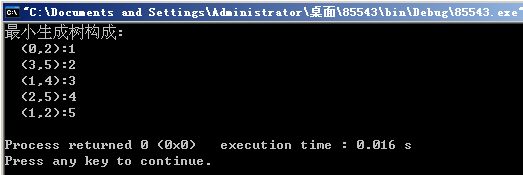

（3）Dijkstra算法的验证

#include 
#include 
#include "graph.h"
#define MaxSize 100
void Ppath(int path[],int i,int v)  //前向递归查找路径上的顶点
{
    int k;
    k=path[i];
    if (k==v)  return;          //找到了起点则返回
    Ppath(path,k,v);            //找顶点k的前一个顶点
    printf("%d,",k);            //输出顶点k
}
void Dispath(int dist[],int path[],int s[],int n,int v)
{
    int i;
    for (i=0; i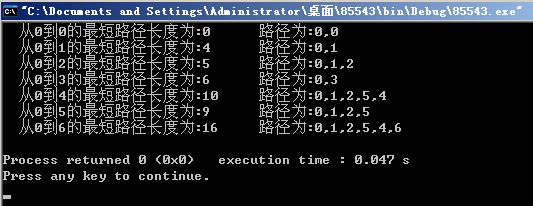

（4）Floyd算法验证

#include 
#include 
#include "graph.h"
#define MaxSize 100
void Ppath(int path[][MAXV],int i,int j)  //前向递归查找路径上的顶点
{
    int k;
    k=path[i][j];
    if (k==-1) return;  //找到了起点则返回
    Ppath(path,i,k);    //找顶点i的前一个顶点k
    printf("%d,",k);
    Ppath(path,k,j);    //找顶点k的前一个顶点j
}
void Dispath(int A[][MAXV],int path[][MAXV],int n)
{
    int i,j;
    for (i=0; i路径长度:%d 路径:",i,j,A[i][j]);
                printf("%d,",i);    //输出路径上的起点
                Ppath(path,i,j);    //输出路径上的中间点
                printf("%d\n",j);   //输出路径上的终点
            }
        }
}
void Floyd(MGraph g)
{
    int A[MAXV][MAXV],path[MAXV][MAXV];
    int i,j,k;
    for (i=0; iA[i][k]+A[k][j])
                {
                    A[i][j]=A[i][k]+A[k][j];
                    path[i][j]=k;
                }
    }
    Dispath(A,path,g.n);   //输出最短路径
}
int main()
{
    MGraph g;
    int A[4][4]=
    {
        {0,  5,INF,7},
        {INF,0,  4,2},
        {3,  3,  0,2},
        {INF,INF,1,0}
    };
    ArrayToMat(A[0], 4, g);
    Floyd(g);
    return 0;
}

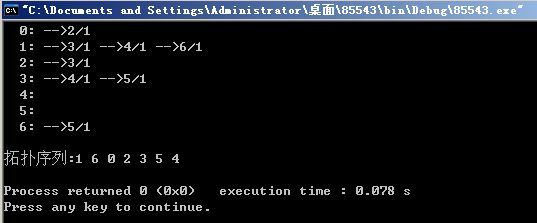
（5）拓扑排序算法验证

#include 
#include 
#include "graph.h"

void TopSort(ALGraph *G)
{
    int i,j;
    int St[MAXV],top=-1;            //栈St的指针为top
    ArcNode *p;
    for (i=0; in; i++)          //入度置初值0
        G->adjlist[i].count=0;
    for (i=0; in; i++)          //求所有顶点的入度
    {
        p=G->adjlist[i].firstarc;
        while (p!=NULL)
        {
            G->adjlist[p->adjvex].count++;
            p=p->nextarc;
        }
    }
    for (i=0; in; i++)
        if (G->adjlist[i].count==0)  //入度为0的顶点进栈
        {
            top++;
            St[top]=i;
        }
    while (top>-1)                  //栈不为空时循环
    {
        i=St[top];
        top--;              //出栈
        printf("%d ",i);            //输出顶点
        p=G->adjlist[i].firstarc;   //找第一个相邻顶点
        while (p!=NULL)
        {
            j=p->adjvex;
            G->adjlist[j].count--;
            if (G->adjlist[j].count==0)//入度为0的相邻顶点进栈
            {
                top++;
                St[top]=j;
            }
            p=p->nextarc;       //找下一个相邻顶点
        }
    }
}

int main()
{
    ALGraph *G;
    int A[7][7]=
    {
        {0,0,1,0,0,0,0},
        {0,0,0,1,1,0,1},
        {0,0,0,1,0,0,0},
        {0,0,0,0,1,1,0},
        {0,0,0,0,0,0,0},
        {0,0,0,0,0,0,0},
        {0,0,0,0,0,1,0}
    };
    ArrayToList(A[0], 7, G);
    DispAdj(G);
    printf("\n");
    printf("拓扑序列:");
    TopSort(G);
    printf("\n");
    return 0;
}