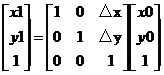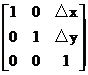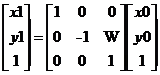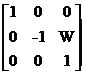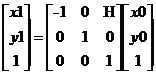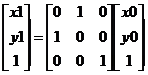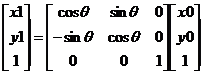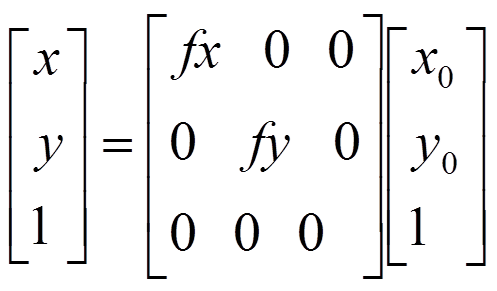【数字图像处理】几何变换

 

目录

图像的平移变换

图像的镜像变换

图像的转置变换

图像的旋转

图像的转置变换

 

一、图像的平移变换

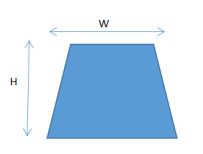
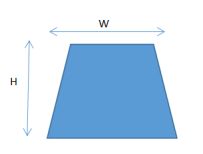
　　设图像的高度为H，宽度为W，如下所示：

          　　　　　　　　　　　　　　　　

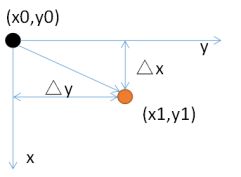
我们知道，图像是由像素组成的，而像素的集合就相当于一个二维的矩阵，每一个像素都有一个“位置”，也就是像素都有一个坐标。假设原来的像素的位置坐标为（x0,y0），经过平移量（△x，△y）后，坐标变为（x1,y1），如下所示：

 　　　　　　　　　　　　　　　　　　　　

用数学式子表示可以表示为：

　　　　　　　　　　　　　　x1 = x0 + △x,

　　　　　　　　　　　　　　y1 = y0 + △y；

用矩阵表示为：

            　　　　　　

本来使用二维矩阵就可以了的，但是为了适应像素、拓展适应性，这里使用三位的向量。

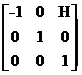
式子中，矩阵：

        　　　　　  　

称为平移变换矩阵（因子），△x和△y为平移量。

这里将变换矩阵变为三行三列可以满足所有几何变换要求。

 

 

 

 

矩阵：称为坐标系矩阵，将二维图像变为三维图像，多常数1。

此外，我们也知道了，图像的高度H其实也就是像素的行数，对于坐标1≤X≤H；图像的长度也就是像素的列数，对应坐标1≤Y≤W。

对于原图中被移出图像显示区域的点通常也有两种处理方法：直接丢弃或者通过加目标图像的尺寸〈将新生成的图像宽度增加TxTx，高度增加TyTy〉的方法使新图像中能够包含这些点。

 

二、图像的镜像变换

　　图像的镜像变换分为水平镜像和垂直镜像。水平镜像即将图像左半部分和右半部分以图像坚直中轴线为中心轴进行对换；而竖直镜像则是将图像上半部分和下半部分以图像水平中轴线为中心轴进行对换.

下面分别进行这两种镜像的介绍，首先说明一下，无论是水平镜像还是垂直镜像，镜像后高度和宽度都不变。

               　　　　　　　　　

       　　　　　　 H图像的高度，关联x          W：图像的宽度，关联y

　　·水平镜像操作：以原图像的垂直中轴线为中心，将图像分为左右两部分进行对称变换。示意图如下所示：

 　　　　　　　　　　　　　　　　　　

　　水平镜像中，原图中的（x0,y0）经过水平镜像后，坐标变成了（x0,W-y0），用数学公式表达就是：

　　　　　　　　　　x1 = x0,

　　　　　　　　　　y1 = W-y0 ;

写成矩阵就是：

                　　　　

也就是说，水平镜像变换矩阵（因子）为：

                        　　

 

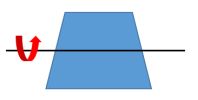
　·垂直镜像操作：以原图像的水平中轴线为中心，将图像分为上下两部分进行对称变换。示意图如下所示：

 　　　　　　　　　　　　

　　垂直镜像中，原图中的（x0,y0）经过垂直镜像后，坐标变成了（H-x0,y0），用数学公式表达就是：

　　　　　　　　x1 = H - x0,

　　　　　　　　y1 = y0 ;

写成矩阵就是：

                　　　　

也就是说，垂直镜像变换矩阵（因子）为：

                        

 

三、图像的转置变换

　　图像的转置就是将图像像素的x坐标和y坐标互换。这样将改变图像的高度和宽度，转置后图像的高度和宽度也将互换。

图像的转置用数学公式描述就是：

   　　　　　　x1 = y0,

                            y1 = x0;

写出矩阵如下所示：

 　　　　　　　　

 

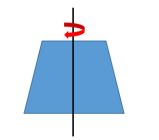
四、图像的旋转

　　一般情况下，旋转操作会有一个旋转中心，这个旋转中心一般为图像的中心，旋转之后图像的大小一般会发生改变。图像像素原来的坐标为（x0,y0），（顺时针）选择Θ角度后得到（x1,y1），用数学公式表达如下所示：

             x1 = x0·cosΘ + y0·sinΘ，

             y1 = -x0·sinΘ + y0·cosΘ；

用矩阵表示如下所示：

 　　　　

 

五、图像的缩放

图像的比例缩放变换是指给定的图像在x轴方向按比例缩放f_x倍，在y轴方向缩放f_y倍，从而获得一幅新的图象。比例缩放前后两点P₀(x₀,y₀)、P(x,y)之间的关系用矩阵形式可以表现为：

数学公式表达：

       x1 = x0·Fx，

       y1 = -y0·Fy；

在图像放大的正变换中，会出现很多的空格。因此，需要对放大后所多出来的空格填入适当的像素值。一般采用最邻近插值和线性插值法。

refer：

数字图像处理笔记与体会（三）——图像的几何变换

图像的几何变换