神经网络模型介绍
本文在介绍神经网络算法模型基础知识的同时,详细阐述了正向传播神经网络的计算过程。
斯坦福大学教授Andrew Ng(吴恩达)在Coursera网课平台上开设的Machine Learning课程,非常适合机器学习新手入门,看过之后有种豁然开朗的感觉。但这门课程是英文讲解的,况且对于快速理解神经网络算法来讲,观看视频课程全面学习Machine Learning的知识体系,效率自然不如阅读专题文章。这是我花费精力写这篇文章的主要原因。本文结构与算法描述方式也主要借鉴于Andrew Ng的课程。只是在细节的地方做了些调整和补充。在这里提前做出说明,避免误被控诉为抄袭。
写本文之前,我查阅了大量网络上相关的文章。发现这些文章大多存在两个极端:一部分太注重于解释神经网络的感性理解,忽略了数学基础,太过简单;另一部分则又过于学术化,大量的复杂公式推导,让很多感兴趣的读者望而却步。我以为,尽管神经网络听上去很深奥,但其实要理解并掌握它的算法原理,并非那么困难。因此,本文想要从感性理解和理性认知两者中间找到合适的平衡,暂且跳过复杂的参数求解过程,从简单的理论出发,一步步阐述神经网络的基本计算方式,让读者可以快速对神经网络算法有个比较直观的认识。
建议英文基础较好,并且有精力的读者学习Andrew的这门课程,我将链接附在这里:https://www.coursera.org/learn/machine-learning
1.神经网络算法的创造缘由
在基础机器学习中,Linear Regression和Logistic Regression都能够拟合输入和输出之间的定量关系,并根据新的输入预测输出值或者进行分类。那为什么还需要神经网络这样的复杂算法呢?主要有两方面的原因:一是现实生活中的很多问题并非线性的。二是在Linear Regression和Logistic Regression模型中,当输入特征的数量比较大时,模型参数的解算效率会非常低。并且随着输入特征数量的增长,参数解算效率以指数形式降低,非常不利于模型学习和应用。
1.1 非线性问题
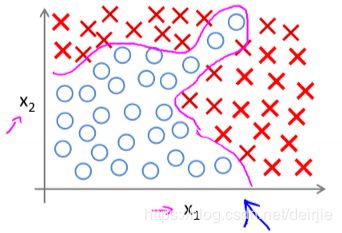
非线性问题比线性问题要复杂的多,但却是现实世界中的最常见的问题形式。对于非线性问题,Linear Regression和Logistic Regression不能达到很好的效果。简单举个例子。假设有两个输入要素,分别是 x 1 , x 2 ∈ R x_1, x_2 ∈ R x1,x2∈R,下图表示了 x 1 x_1 x1和 x 2 x_2 x2构成的两个不同类别的点分布情况。可以看到,这两个类别是没有办法用一条直线进行分割的。现为了区分开这两个类别,在Logistic Regression模型中,就需要引入高阶变量,例如 x 1 x 2 , x 1 2 x 2 , x 1 x 2 2 x_1x_2, x_1^2x_2, x_1x_2^2 x1x2,x12x2,x1x22等等作为新的输入要素加入模型,这首先会带来输入要素的数量增加,且高阶变量自然会让模型变得更加复杂,同时容易引起Overfitting的问题。
1.2 大量特征带来的问题
除了上面讲到的非线性问题导致的特征数量增多的情况,现实生活中的很多问题,其特征本来就是非常多的。计算机视觉问题就是典型的例子。图像通过像素矩阵来表示现实世界的物体,像素矩阵中的点往往非常多,将这些像素点的值作为特征输入模型,庞大的特征数量是显而易见的。而当特征数量上升时,线性回归和逻辑回归模型会让求解变得非常慢。事实上,这个关系根据使用的输入特征阶数的不同,线性回归和逻辑回归模型的参数求解会有 O ( n 2 ) 、 O ( n 3 ) O(n^2)、O(n^3) O(n2)、O(n3)等时间复杂度。传统的输入特征为1~1000时尚可接受,而一个普通 50 ∗ 50 50*50 50∗50的灰度图像像素矩阵,输入特征都是2500个,更别说更大、更复杂的图像了,

2.神经网络模型表示
2.1 神经网络的结构和数学定义
(1)模型结构
神经网络模型包含三个部分:input layer(输入层)、hidden layer(中间层或隐藏层)、output layer(输出层)。其中,hidden layer的层数不固定,在某些简单问题中,hidden layer的层数可能为0,仅有input layer和output layer;在复杂问题中,hidden layer的层数也可能成百上千。

模型中每一层的节点称为“神经元”。位于input layer的神经元对应着训练数据的特征。hidden layer和output layer中的神经元由activation function(激活函数)表达,我们用字母 g g g表示。Activation function有很多种类型,最常用是sigmoid函数,它的表达式如下:
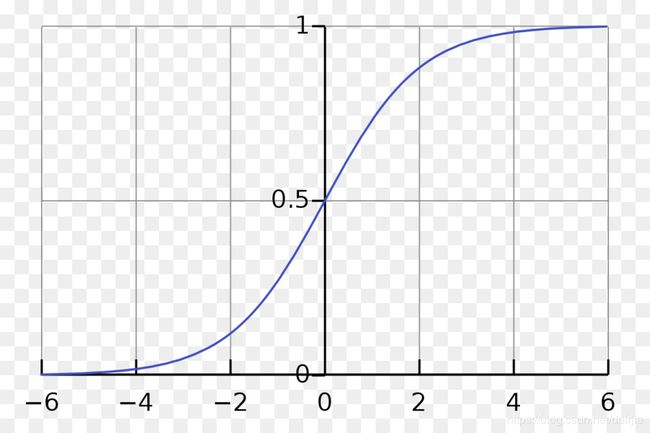
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
sigmoid函数图像如下图所示。当 x > > 0 x>>0 x>>0时, f ( x ) f(x) f(x)无限逼近于1;当 x < < 0 x<<0 x<<0时, f ( x ) f(x) f(x)无限逼近于0;当 x = 0 x=0 x=0时, f ( x ) = 0.5 f(x)=0.5 f(x)=0.5。
(2)训练样本数据
为了深入阐述神经网络模型算法过程,我们来定义一些需要用到的数学变量和符号。
我们用 x x x表示输入的特征向量, x i x_i xi表示单独的特征变量。 y y y表示真实类别标签向量, y i y_i yi对应单独的真实类别,为了简单起见,我们先从二元分类讲起,也就是说 y ∈ { 0 , 1 } y∈\{0,1\} y∈{0,1}。假如,我们想训练一个神经网络模型,根据房子的某些特征自动判断该房子是否为别墅,那么特征向量 x x x就可以表示为:
x = [ x 1 = 卧 室 数 目 x 2 = 客 厅 面 积 x 3 = 总 体 面 积 . . . ] x=\begin{bmatrix}x_1=卧室数目\\x_2=客厅面积\\x_3=总体面积\\...\end{bmatrix} x=⎣⎢⎢⎡x1=卧室数目x2=客厅面积x3=总体面积...⎦⎥⎥⎤
其中,卧室数目、客厅面积、总体面积等等数据都是特征变量,它们共同衡量了房子的属性。并且,我们定义当 y = 1 y=1 y=1时,表示该房子为别墅;当 y = 0 y=0 y=0时,表示房子为其他类型。这样,我们就可以收集整理一些如下表所示的训练样本数据:
| 卧室数目( x 1 x_1 x1) | 客厅面积( x 2 x_2 x2 ) | 总体面积( x 3 x_3 x3) | … | 别墅? |
|---|---|---|---|---|
| 8 | 60 | 300 | … | 1 |
| 2 | 20 | 90 | … | 0 |
| … | … | … | … | … |
| 10 | 80 | 400 | … | 1 |
(3)模型数学表示
为了方便使用数学表示,我们不单独为input layer、hidden layer和output layer定义数学表示,而是使用 a = { a ( 1 ) , a ( 2 ) , a ( 3 ) , . . . , a ( n ) } a=\{a^{(1)}, a^{(2)}, a^{(3)},...,a^{(n)}\} a={a(1),a(2),a(3),...,a(n)}来表示从左到右的各个层。例如在简单的三层神经网络模型中, a ( 1 ) a^{(1)} a(1)表示输入层, a ( 2 ) a^{(2)} a(2)表示中间层, a ( 3 ) a^{(3)} a(3)表示输出层。用 θ j ( i ) \theta_j^{(i)} θj(i)来表示各层对应的权重参数, i i i表示层号, j j j表示该层中的神经元。由此,一个简单的三层神经网络模型中,各个结构的数学可以表示如下图:

2.2 Forward Propagation
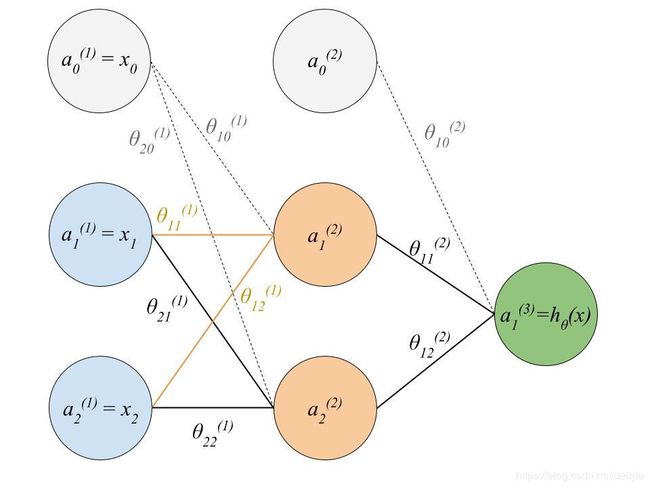
我们以Forward Propagation(正向传递)计算过程为例,详细介绍神经网络模型当中的数学计算。为了简单起见,我们以下图中展示的神经网络模型为例。这里我们先暂时不介绍模型参数求解相关方法,而是假设已经计算得到了所有的模型参数值。

在这个模型中,第一层有2个神经元,分别用 x 1 , x 2 x_1, x_2 x1,x2表示;第二层包含2个神经元,分别用 a 1 ( 2 ) , a 2 ( 2 ) a_1^{(2)}, a_2^{(2)} a1(2),a2(2)表示;第三层只有1个神经元,用 h θ ( x ) h_\theta(x) hθ(x)表示(我们用 y y y表示了数据的真实类型,这里便用 h θ ( x ) h_\theta(x) hθ(x)表示模型的输出值,以示区别);各神经元之间的连接权重参数 θ \theta θ在图中有详细表示。
由于神经网络模型计算需要使用到Linear Regression的参数乘积运算,而在参数乘积运算中:
h θ ( x ) = θ T x = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n 其 中 , x = [ x 1 x 2 ] , θ = [ θ 0 θ 1 θ 2 ] h_\theta(x)=\theta^Tx=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n\\ 其中,\\ x=\begin{bmatrix}x_1\\x_2\end{bmatrix}, \theta=\begin{bmatrix}\theta_0\\\theta_1\\\theta_2\end{bmatrix} hθ(x)=θTx=θ0+θ1x1+θ2x2+...+θnxn其中,x=[x1x2],θ=⎣⎡θ0θ1θ2⎦⎤
为了让 x x x和 θ \theta θ两个向量“对齐”,便于方便地使用向量运算方法表示计算过程,我们人为加入值为1的常量 x 0 x_0 x0,于是上面的式子就变为:
h θ ( x ) = θ T x = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n 其 中 , x = [ x 0 x 1 x 2 ] , θ = [ θ 0 θ 1 θ 2 ] h_\theta(x)=\theta^Tx=\theta_0x_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n\\ 其中,\\ x=\begin{bmatrix}x_0\\x_1\\x_2\end{bmatrix}, \theta=\begin{bmatrix}\theta_0\\\theta_1\\\theta_2\end{bmatrix} hθ(x)=θTx=θ0x0+θ1x1+θ2x2+...+θnxn其中,x=⎣⎡x0x1x2⎦⎤,θ=⎣⎡θ0θ1θ2⎦⎤
同样,我们也在神经网络模型中,需要进行参数乘积运算的地方加入bias神经元,如下图所示:
最后,我们假设使用的activation function为sigmoid函数,也就是 g ( x ) = s i g m o i d ( x ) g(x)=sigmoid(x) g(x)=sigmoid(x),于是Forward Propagation的计算过程如下:
-
计算第一层变量与对应参数的乘积,作为第二层的输入。
( θ 1 ( 1 ) ) T x = θ 10 ( 1 ) x 0 + θ 11 ( 1 ) x 1 + θ 12 ( 1 ) x 2 ( θ 2 ( 1 ) ) T x = θ 20 ( 2 ) x 0 + θ 21 ( 1 ) x 1 + θ 22 ( 1 ) x 2 (\theta_1^{(1)})^Tx=\theta_{10}^{(1)}x_0+\theta_{11}^{(1)}x_1+\theta_{12}^{(1)}x_2 \\ (\theta_2^{(1)})^Tx=\theta_{20}^{(2)}x_0+\theta_{21}^{(1)}x_1+\theta_{22}^{(1)}x_2 (θ1(1))Tx=θ10(1)x0+θ11(1)x1+θ12(1)x2(θ2(1))Tx=θ20(2)x0+θ21(1)x1+θ22(1)x2 -
使用sigmoid函数计算第二层中各神经元的值:
s i g m o i d ( θ T x ) = 1 1 + e − θ T x a 1 ( 2 ) = s i g m o i d ( θ 1 ( 1 ) ) T x a 2 ( 2 ) = s i g m o i d ( θ 2 ( 1 ) ) T x sigmoid(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} \\ a_1^{(2)}=sigmoid(\theta_1^{(1)})^Tx \\ a_2^{(2)}=sigmoid(\theta_2^{(1)})^Tx sigmoid(θTx)=1+e−θTx1a1(2)=sigmoid(θ1(1))Txa2(2)=sigmoid(θ2(1))Tx -
将第二层计算结果与对应参数的乘积,作为第三层的输入:
( θ 1 ( 2 ) ) T a = θ 10 ( 2 ) a 0 ( 2 ) + θ 11 ( 2 ) a 1 ( 2 ) + θ 12 ( 2 ) a 2 ( 2 ) (\theta_1^{(2)})^Ta=\theta_{10}^{(2)}a_0^{(2)}+\theta_{11}^{(2)}a_1^{(2)}+\theta_{12}^{(2)}a_2^{(2)} (θ1(2))Ta=θ10(2)a0(2)+θ11(2)a1(2)+θ12(2)a2(2) -
使用sigmoid函数计算第三层的值:
h θ ( x ) = s i g m o i d ( ( θ 1 ( 2 ) ) T a ) = 1 1 + e − ( θ 1 ( 2 ) ) T a h_\theta(x)=sigmoid((\theta_1^{(2)})^Ta)=\frac{1}{1+e^{-(\theta_1^{(2)})^Ta}} hθ(x)=sigmoid((θ1(2))Ta)=1+e−(θ1(2))Ta1 -
根据 h θ ( x ) h_\theta(x) hθ(x)的值,做出判断。
是的,尽管神经元增加了以后,整个运算会看起来很复杂,但是模型当中的计算过程实际上就是这么简单。使用不同的activation function,只需要替换以上算法过程中的sigmoid函数就可以。增加hidden layer的层数,也不过是重复以上迭代过程而已。
2.3 神经网络模型表示逻辑关系
为什么神经网络模型按照上文介绍的计算方法,就能够表示非线性问题?下面我们通过神经网络模型表示逻辑关系的例子,来看看神经网络模型的“奇妙”之处。
逻辑关系包含“AND”、“OR”、“NOT”、“XOR”4种简单运算。现实世界中错综复杂的问题,常常可以用这些简单逻辑运算的排列组合来表达。
(1)“AND”关系的表示
“AND”关系定义为:
x 1 , x 2 ∈ { 0 , 1 } , y = x 1 A N D x 2 x_1, x_2 ∈ \{0,1\},\ \ \ \ y=x_1\ AND\ x_2 x1,x2∈{0,1}, y=x1 AND x2
只有 x 1 x_1 x1和 x 2 x_2 x2同时为1时, h θ ( x ) h_\theta(x) hθ(x)才为1,否则 h θ ( x ) h_\theta(x) hθ(x)为0。
用下图所示的神经网络就可以表示“AND”关系:
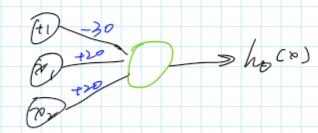
图中表示的参数并不是唯一的。根据Forward Propagation,这个神经网络的计算结果可以表示为:
h θ ( x ) = g ( − 30 + 20 x 1 + 20 x 2 ) h_\theta(x)=g(-30+20x_1+20x_2) hθ(x)=g(−30+20x1+20x2)
实际上,这样的简单神经网络模型等同于logistic regression。代入 x 1 , x 2 x_1,x_2 x1,x2的值检验一下模型计算结果,可以得到如下表所示关系:
| x 1 x_1 x1 | x 2 x_2 x2 | h θ ( x ) h_\theta(x) hθ(x) |
|---|---|---|
| 0 | 0 | g ( − 30 ) ≈ 0 g(-30)≈0 g(−30)≈0 |
| 0 | 1 | g ( − 10 ) ≈ 0 g(-10)≈0 g(−10)≈0 |
| 1 | 0 | g ( − 10 ) ≈ 0 g(-10)≈0 g(−10)≈0 |
| 1 | 1 | g ( + 10 ) ≈ 1 g(+10)≈1 g(+10)≈1 |
可以看到,只有 x 1 , x 2 x_1,x_2 x1,x2同时为1时, h ( θ ) h(\theta) h(θ)才能等于1。因此,这个神经网络模型正确表示出了“AND”逻辑运算。
(2)“OR”关系的表示
“OR”关系定义为:
x 1 , x 2 ∈ { 0 , 1 } , y = x 1 O R x 2 x_1, x_2 ∈ \{0,1\},\ \ \ \ y=x_1\ OR\ x_2 x1,x2∈{0,1}, y=x1 OR x2
当 x 1 x_1 x1和 x 2 x_2 x2有一个等于1时, y y y就等于1,否则 y y y等于0。
这个模型同样简单,可以表示为:
h θ ( x ) = g ( − 10 + 20 x 1 + 20 x 2 ) h_\theta(x)=g(-10+20x_1+20x_2) hθ(x)=g(−10+20x1+20x2)
代入 x 1 , x 2 x_1,x_2 x1,x2,可以发现该模型能正确表示“OR”逻辑运算。具体计算结果如下表所示:
| x 1 x_1 x1 | x 2 x_2 x2 | h θ ( x ) h_\theta(x) hθ(x) |
|---|---|---|
| 0 | 0 | g ( − 10 ) ≈ 0 g(-10)≈0 g(−10)≈0 |
| 0 | 1 | g ( + 10 ) ≈ 1 g(+10)≈1 g(+10)≈1 |
| 1 | 0 | g ( + 10 ) ≈ 1 g(+10)≈1 g(+10)≈1 |
| 1 | 1 | g ( + 10 ) ≈ 1 g(+10)≈1 g(+10)≈1 |
(3)“NOT”关系的表示
“NOT”即“非”或“否”,关系表示为:
x 1 ∈ { 0 , 1 } , y = N O T x 1 x_1∈ \{0,1\},\ \ \ \ y=NOT\ x_1 x1∈{0,1}, y=NOT x1
也就是当 y y y值总是 x x x值的反面。用神经网络模型表示“NOT”关系就更容易了,如下图所示:
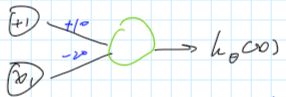
这个神经网络可以表示为:
h θ ( x ) = g ( 10 − 20 x 1 ) h_\theta(x)=g(10-20x_1) hθ(x)=g(10−20x1)
代入 x 1 x_1 x1的值,可以发现该模型能正确表示“NOT”逻辑运算。具体计算结果如下表所示:
| x 1 x_1 x1 | h θ ( x ) h_\theta(x) hθ(x) |
|---|---|
| 0 | g ( + 10 ) ≈ 1 g(+10) ≈ 1 g(+10)≈1 |
| 1 | g ( − 20 ) ≈ 0 g(-20) ≈ 0 g(−20)≈0 |
(4)“XNOR”关系的表示
“XNOR”在中文中常被翻译为“异或”,它的数学定义如下:
x 1 , x 2 ∈ { 0 , 1 } , y = x 1 X O R x 2 x_1, x_2 ∈ \{0,1\},\ \ \ \ y=x_1\ XOR\ x_2 x1,x2∈{0,1}, y=x1 XOR x2
当 x 1 , x 2 x_1, x_2 x1,x2同为0或者同为1时, y = 1 y=1 y=1;当 x 1 , x 2 x_1, x_2 x1,x2中有一个为1,另一个为0时, y = 0 y=0 y=0。
在表示“AND”、“OR”和“NOT”关系时,我们都仅仅使用了结构非常简单的神经网络模型。而在表示“XNOR”关系时,以上的简单神经网络模型就不够用了,需要加入其他的神经元。如下图所示:
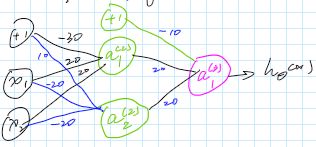
我们来计算一下:
a 1 ( 2 ) = g ( − 30 + 20 x 1 + 20 x 2 ) a 2 ( 2 ) = g ( 10 − 20 x 1 − 20 x 2 ) 并 且 h θ ( x ) = a 1 ( 3 ) = g ( − 10 + 20 a 1 ( 2 ) + 20 a 1 ( 2 ) ) a_1^{(2)} = g(-30+20x_1+20x_2) \\ a_2^{(2)} = g(10-20x_1-20x_2) \\ 并且\\ h_\theta(x) =a_1^{(3)}= g(-10+20a_1^{(2)}+20a_1^{(2)}) a1(2)=g(−30+20x1+20x2)a2(2)=g(10−20x1−20x2)并且hθ(x)=a1(3)=g(−10+20a1(2)+20a1(2))
同样,用表格的形式分别代入 x 1 , x 2 x_1, x_2 x1,x2的值,对应关系如下:
| x 1 x_{1} x1 | x 2 x_2 x2 | a 1 ( 2 ) a_1^{(2)} a1(2) | a 2 ( 2 ) a_2^{(2)} a2(2) | h θ ( x ) h_\theta(x) hθ(x) |
|---|---|---|---|---|
| 0 | 0 | g ( − 30 ) ≈ 0 g(-30) ≈ 0 g(−30)≈0 | g ( + 10 ) ≈ 1 g(+10) ≈ 1 g(+10)≈1 | g ( + 10 ) ≈ 1 g(+10) ≈ 1 g(+10)≈1 |
| 0 | 1 | g ( − 10 ) ≈ 0 g(-10)≈0 g(−10)≈0 | g ( − 10 ) ≈ 0 g(-10)≈0 g(−10)≈0 | g ( − 10 ) ≈ 0 g(-10)≈ 0 g(−10)≈0 |
| 1 | 0 | g ( − 10 ) ≈ 0 g(-10)≈ 0 g(−10)≈0 | g ( − 10 ) ≈ 0 g(-10) ≈ 0 g(−10)≈0 | g ( − 10 ) ≈ 0 g(-10) ≈ 0 g(−10)≈0 |
| 1 | 1 | g ( + 10 ) ≈ 1 g(+10) ≈ 1 g(+10)≈1 | g ( − 30 ) ≈ 0 g(-30) ≈ 0 g(−30)≈0 | g ( + 10 ) ≈ 1 g(+10) ≈ 1 g(+10)≈1 |
通过上面的几个神经网络实现逻辑运算的例子可以看出,即便是不使用中间层,神经网络就能够正确表示出“AND”、“OR”和“NOT”逻辑运算关系。“XNOR”关系的表达也仅仅只需要引入两个中间层的神经元而已。那么,当中间层的数目不断增加,神经元的数量不断增加,这些简单逻辑关系不断组合,就能够表达出错综复杂的“非线性”关系。这正是神经网络模型的奥妙之处。当然,这并不表示神经元越多、结构越复杂,就一定越好。结构越复杂,运算所需要的代价就越大。面向不同的应用、不同的数据,选择“最优”的神经网络模型结构,才是最佳策略。选择“最优”的过程实际上就是神经网络的参数调节过程,常被称为“调参”。具体如何对神经网络模型进行“调参”,本文就不作展开了,感兴趣的朋友可以通过机器学习课程,或者网络上的学习资源进行深入研究。
3. 多类别分类
上面我们讨论的都是二元分类问题,输出层只有一个神经元,输出结果要么是1,要么是0。现实世界中的分类应用要复杂的多。例如,一幅图片有可能被分类为猫、狗、大象等等类别。那么,如何用一个神经网络模型来同时得出多种不同的分类结果呢?
事实上,我们采用的策略非常简单,即在输出层中设置多个神经元,每个输出层代表一个类别。如下图所示。
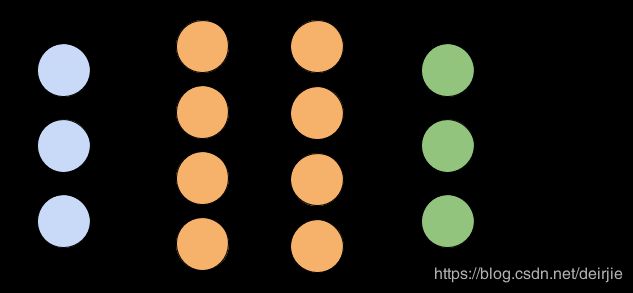
在上图所示的神经网络结构中,输出层中的每个神经元都会有一个计算结果,我们综合比较每个结果数值,选择值最大的那个神经元所对应的类别,作为最终的计算类别。例如,假设我们输入某个新图像 x i x_i xi,模型计算得到如下结果:
h ( θ ) = [ 0.2 0.3 0.7 ] h(\theta)=\begin{bmatrix}0.2\\0.3\\0.7\\\end{bmatrix} h(θ)=⎣⎡0.20.30.7⎦⎤
那么,我们就取0.7那个神经元所对应的类别,作为图像 x i x_i xi的类别。这里这个类别为“大象”。
本文暂且假设所有参数已知,详细介绍了神经网络内部是如何进行运算并作出类别判断的。具体涉及的cost function, gradient descent等参数求解的算法,将在未来作出补充。有较好英文基础的朋友,也可以直接学习Andrew Ng的课程视频。