Boost Graph Library 快速入门

Boost Graph Library 快速入门

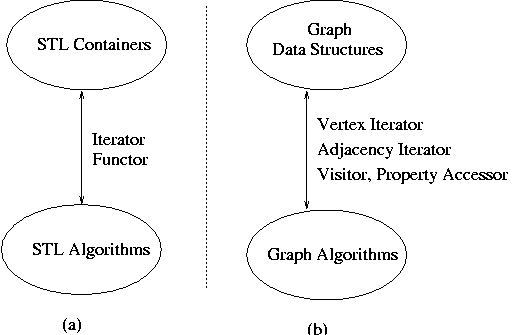
   图领域的数据结构和算法在某些方面比容器更为复杂，图算法在图中移动有着众多的路线，而STL使用的抽象迭代器接口不能有效的支持这些。作为替换，我们为图提供了一个的抽象的结构，其与容器迭代器的目的类似（尽管迭代器扮演着更大的角色）。图1 描述了STL 和BGL 之间的对比
                        图1: The analogy between the STL and the BGL.

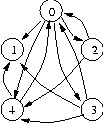
  图由一系列顶点vertices，以及连接顶点的边edges组成. 如图2描述了一个拥有5个顶点和11条边的有向图directed graph. 离开一个顶的边称为该点的out-edges。边 {(0,1),(0,2),(0,3),(0,4)} 都是节点0的out-edges ,进入一个顶点的边称为该点的in-edges , 边{(0,4),(2,4),(3,4)} 是节点0的in-edges

                             图2 一个有向图例子

在后面的章节中，我们使用BGL构造上图并展示各种操作。全部的代码可以在examples/quick_tour.cpp  中找到，下面每个章节都是这个例子文件的一个片断。

构造一个图

在这个例子中，我们将使用BGL 邻接表adjacency_list 类来示范BGL接口中的主要概念.adjacency_list类提供了典型邻接表数据结构的一个泛型版本. adjacency_list 是一个拥有6个模板参数的模板类。但我们只使用了前3个参数，剩余的3个使用默认参数。头两个模板参数(vecS, vecS)分别用来描述离开顶点的out-edges边和图中顶点的集合所使用的数据结构，(阅读 Choosing the Edgelist and VertexList 章节可以获得更多关于平衡不同数据结构的信息) 第三个参数, 使用bidirectionalS表示选择一个可访问出、入边的有向图，directedS 为选择一个仅提供出边的有向图。undirectedS 表示选择一个无向图

  一旦我们选定了图的类型，我们可以创建一个图2所示的图。声明一个图对象，使用 MutableGraph 接口中的add_edge() 函数来填充边，在这个例子中我们简单的使用 pairs 数组edge_array来建立边在这个例子中我们简单的使用 pairs 数组edge_array来建立边

#include // for std::cout
#include // for std::pair
#include // for std::for_each
#include
#include
#include
using namespace boost;

int main(int,char*[])
{
    typedef adjacency_list Graph;
    // Make convenient labels for the vertices
    enum { A, B, C, D, E, N }; //代表 0 ，1，2，3，4 顶点
    const int num_vertices = N;
    const char* name = "ABCDE";
    //图中的边
    typedef std::pair Edge;
    Edge edge_array[] = { Edge(A,B), Edge(A,D), Edge(C,A), Edge(D,C),
                            Edge(C,E), Edge(B,D), Edge(D,E) };
    const int num_edges = sizeof(edge_array)/sizeof(edge_array[0]);
    // 创建一个拥有5个顶点的图对象
    Graph g(num_vertices);
    // 给图对象添加边
    for (int i = 0; i < num_edges; ++i)
      add_edge(edge_array[i].first, edge_array[i].second, g);
   return 0;
}

  我们可以使用图的edge iterator constructor 构造函数来代替为每个边调用add_edge()函数，这种方法
更具代表性比add_edge()更有效率, edge_array 指针可以被视为迭代器,所以我们可以传递数组开始和结束的指针给图构造函数
Graph g(edge_array, edge_array + sizeof(edge_array) / sizeof(Edge), num_vertices);
同样可以使用 MutableGraph 接口的add_vertex()和remove_vertex() 来为图添加和删除顶点，
而不是一开始就创建一个拥有一定数目顶点的图

访问顶点集合

  现在我们创建了一个图，我们可以使用图接口访问图数据，首先我们可以通过 VertexListGraph 接口的vertices() 函数来访问图中所有的顶点。这个函数返回一个顶点迭代器的std::pair 类型（第一个迭代器指向顶点的开始，第二个迭代器指向顶点的结束）。提领一个顶点迭代器放回一个顶点对象。顶点迭代器的类型可由graph_traits 类取得，值得注意的是不同的图类型可能有不同的顶点迭代器类型，这也是为什么我们需要graph_traits 类的原因。给定一个图类型，graph_traits类能提供该图的vertex_iterator类型，下面的例子打印了图中每个顶点的索引。所有的顶点和边属性，以及索引，可以通过property map 对象访问。property_map 类可用来获得指定属性(通过指定BGL预定义的vertex_index_t来取得索引)的property map 类型，通过调用函数get(vertex_index, g) 来获得图当前的property map对象
int main(int,char*[])
{
    //获得顶点索引的 property map
    typedef property_map::type IndexMap;
    IndexMap index = get(vertex_index, g);

    std::cout << "vertices(g) = ";
    typedef graph_traits::vertex_iterator vertex_iter;
    std::pair vp;
    for (vp = vertices(g); vp.first != vp.second; ++vp.first)
            std::cout << index[*vp.first] << " ";
    std::cout << std::endl;
    return 0;
}
输出结果:
vertices(g) = 0 1 2 3 4

访问边集合

   一个图的边集合可以使用 EdgeListGraph接口中的 edges()函数访问。与vertices() 函数类似，这个函数也返回一对迭代器，但在这里的迭代器是边迭代器edge iterators。提领边迭代器可以获得一个边对象，调用source()和target()函数可以取得边连接的两个顶点。这次我们使用tie()辅助函数,而不是为迭代器声明一个pair类型，这个便利的函数可以用来分开std::pair 到两个分离的变量，这里是ei 和 ei_end,这样比创建一个std::pair 类型方便。这也是我们为BGL选择的方法

int main(int,char*[])
{
    std::cout << "edges(g) = ";
    graph_traits::edge_iterator ei, ei_end;
    for (tie(ei, ei_end) = edges(g); ei != ei_end; ++ei)
    std::cout << "(" << index[source(*ei, g)]<< "," << index[target(*ei, g)] << ") ";
    std::cout << std::endl;
    return 0;
}
输出结果:
edges(g) = (0,1) (0,2) (0,3) (0,4) (2,0) (2,4) (3,0)(3,1) (3,4) (4,0) (4,1)

邻接结构

   在下面的例子中我们通过观察一个特殊的顶点来展示图的邻接结构，我们将看到顶点的 in-edges, out-edges, 以及他的邻接点adjacent vertices. 我们将这些封装到一个"exercise vertex" 函数对象，并针对图的每个顶点调用它。为了示范BGL同STL协作的能力, 我们使用STL的for_each() 函数迭代每个顶点并调用此函数.
int main(int,char*[])
{
    std::for_each(vertices(g).first, vertices(g).second,
    exercise_vertex(g));
    return 0;
}
 当我们访问每个顶点的信息时需要使用到图对象，所以我们把exercise_vertex写成一个函数对象而不是函数，在std::for_each()执行期间，使用函数对象可以给我们提供了一个位置来保持对图对象的引用。为了能够处理不同的图对象，我们将此函数对象模板化。这里是exercise_vertex 函数对象的开始
template struct exercise_vertex
{
    exercise_vertex(Graph& g_) : g(g_) {}
    Graph& g;
};

顶点描述符

 在撰写函数对象operator()方法时，我们首先要知道的是图中顶点对象的类型。顶点类型用来声明operator()中的参数。确切的说，我们实际上并不处理顶点对象，而是使用顶点描述符vertex descriptors. 许多图结构（如邻接表adjacency lists）并不需要存储顶点对象，而另一些存储(例如 pointer-linked graphs)，这些不同将被顶点描述符对象的黑箱操作所隐藏。顶点描述符由图类型提供，在后面章节将介绍通过对操作符调用函数out_edges(), in_edges(), adjacent_vertices(),和property map来访问图信息。顶点描述符类型可以通过graph_traits类获得,下面语句中的typename 关键字是必须的，因为在范围操作符::左边(graph_traits类型)由模板参数（Graph类型）确定。下面是我们定义的函数对象
template struct exercise_vertex
{
    typedef typename graph_traits::vertex_descriptor Vertex;
    void operator()(const Vertex& v) const
    {
    }
};

Out-Edges, In-Edges, 和Edge 描述符

   可以通过IncidenceGraph接口中的out_edges()函数来访问一个顶点的out-edges, 这个函数需要两个参数：第一个参数是顶点，第二个是图对象。函数返回一对迭代器，来提供对一个顶点所有out-edges的访问（与vertices()函数返回pair对象类似）。这些迭代器称为out-edge iterators， 提领这些迭代器将返回一个边描述符对象，边描述符跟顶点描述符扮演类似性质的角色,也是图类型提供的黑盒,后面的代码片断按source-target顺序打印了顶点v对应的每个out-edge边上的两个点
template struct exercise_vertex
{
    void operator()(const Vertex& v) const
    {
         //......
        typedef graph_traits GraphTraits;
        typename property_map::type
        index = get(vertex_index, g);

        std::cout << "out-edges: ";
        typename GraphTraits::out_edge_iterator out_i, out_end;
        typename GraphTraits::edge_descriptor e;
        for (tie(out_i, out_end) = out_edges(v, g);out_i != out_end; ++out_i)
        {
            e = *out_i;
            Vertex src = source(e, g), targ = target(e, g);
            std::cout << "(" << index[src] << "," << index[targ] << ") ";
        }
        std::cout << std::endl;
    }
};
对于顶点0 输出结果是:
out-edges: (0,1) (0,2) (0,3) (0,4)

in_edges()  函数位于BidirectionalGraph接口中,此函数可以通过in-edge迭代器访问一个顶点所有的in-edges。 只有当邻接表的Directed(第三个)模板参数设为bidirectionalS 才能使用此函数. 而指定bidirectionalS代替directedS时将会花费更多的空间
template struct exercise_vertex
{
    void operator()(const Vertex& v) const
    {
        //....... 省略与上面重复代码
        std::cout << "in-edges: ";
        typedef typename graph_traits GraphTraits;
        typename GraphTraits::in_edge_iterator in_i, in_end;
        for (tie(in_i, in_end) = in_edges(v,g); in_i != in_end; ++in_i)
        {
            e = *in_i;
            Vertex src = source(e, g), targ = target(e, g);
            std::cout << "(" << index[src] << "," << index[targ] << ") ";
        }
        std::cout << std::endl;
    }
};
对于顶点 0 输出是:
in-edges: (2,0) (3,0) (4,0)

邻接点

 当给出一个顶点的所有的out-edges边时，这些边上的目标点对于源点邻接。有时一个算法不需要关注一个图的边，而是仅关心顶点。因此图形接口AdjacencyGraph 提供了adjacent_vertices()函数来直接访问邻接点。此函数返回一对adjacency iterators ，提领一个邻接点迭代器将会得到领接顶点的顶点描述符。
template struct exercise_vertex
{
    void operator()(Vertex v) const
    {
        //.......
        std::cout << "adjacent vertices: ";
        typename graph_traits::adjacency_iterator ai;
        typename graph_traits::adjacency_iterator ai_end;
        for (tie(ai, ai_end) = adjacent_vertices(v, g);ai != ai_end; ++ai)
               std::cout << index[*ai] << " ";
        std::cout << std::endl;
    }
};

给你的图添加一些颜色

  BGL实现尽可能灵活地适应图的附加属性，举个例子，属性如边的权重存在于在图对象的整个生命周期都，因此让图对象管理这个属性的存储将会带来很多便利；另外，属性如顶点颜色只在某个算法的运行期内需要，将此属性和图对象分开存储将会更好。第一种属性称为内在存储属性，而第二种称为外在存储属性。BGL 在图算法中为两种属性提供了一致的访问接口property map，此接口在章节Property Map Concepts中有详细描述。另外，PropertyGraph 配接器也为获得一个内在存储属性的property map 对象定义了接口

  BGL 邻接表类允许用户通过设置图对象模版参数来指定内在存储属性，如何实现这些在Internal Properties 章节有详细论述。外在存储属性有多种创建方法，尽管他们基本上作为分离参数传递给图算法。一个简单存储外在属性的办法是通过顶点或边的索引来创建一个索引数组。如邻接表中的VertexList模版参数指定为vecS，每个顶点的索引将会自动建立。通过指定vertex_index_t作为模版参数的property map对象来访问这些索引。每个边虽不能自动建立索引。但是可以通过使用属性机制把索引和边联系起来，来索引其他的外在存储属性。

  在下面的例子中，我们创建一个图并执行dijkstra_shortest_paths()算法，完整的源代码在例子examples/dijkstra-example.cpp中。Dijkstra 算法用来计算从起始顶点到其他顶点的最短路径。Dijkstra 算法要求设置每个边的权重和每个顶点的距离，这里我们把权重做为一个内在属性，距离作为外在属性。对于权重属性，我们创建属性类并指定int 作为权重类型，edge_weight_t 作为属性标记(一个BGL预定义的属性标记)。此权重属性类将作为邻接表adjacency_list 的一个模版参数

  选择listS或者vecS类型取决于我要在邻接表中使用的数据结构(可以看 Choosing the Edgelist and VertexList章节)。directedS 类型指定图为有向图（相对的是无向图）。后面的代码展示了一个图类型的声明和初始化，以及带权重属性的边如何传递给（使用迭代器作为参数的）图构造函数（要求随机迭代器）
typedef adjacency_list no_property, property > Graph;
typedef graph_traits::vertex_descriptor Vertex;
typedef std::pair E;

const int num_nodes = 5;
E edges[] = { E(0,2),
E(1,1), E(1,3), E(1,4),
E(2,1), E(2,3),
E(3,4),
E(4,0), E(4,1) };
int weights[] = { 1, 2, 1, 2, 7, 3, 1, 1, 1};
Graph G(edges + sizeof(edges) / sizeof(E), weights, num_nodes);

 对于外部距离属性，我们使用std::vector 来存储， BGL 算法视随机迭代器为property maps。所以我们能够传递距离数组vector迭代器到Dijkstra's 算法。紧接上面的例子，下面的代码创建了一个distance vector, 然后调用Dijkstra's 算法(内部使用了权重属性)，输出结果:
// vector for storing distance property
std::vector d(num_vertices(G));
// get the first vertex
Vertex s = *(vertices(G).first);
// invoke variant 2 of Dijkstra's algorithm
dijkstra_shortest_paths(G, s, distance_map(&d[0]));

std::cout << "distances from start vertex:" << std::endl;
graph_traits::vertex_iterator vi;
for(vi = vertices(G).first; vi != vertices(G).second; ++vi)
std::cout << "distance(" << index(*vi) << ") = "
<< d[*vi] << std::endl;
std::cout << std::endl;

结果是:
distances from start vertex:
distance(0) = 0
distance(1) = 6
distance(2) = 1
distance(3) = 4
distance(4) = 5

使用Visitors扩充图算法

  通常一个库中的算法能够满足你大部分的需求，但事无绝对，例如在前面的章节中，我们使用Dijkstra's 算法来计算到每个顶点的最短路径，但可能我们想记录路径最短的树，可以通过在记录最短路径树中记录每个节点的前驱来实现。
  当然我们最好能够避免重写Dijkstra's 算法，并且只增加记录前辈节点的额外需求[1]，在STL中，可以使用仿函数作为算法的可选参数来提供这种伸缩性。在BGL中，visitors 扮演着类似的角色。Visitor 类似stl仿函数。仿函数只有一个执行函数，但Visitor 拥有更多的方法，每个方法将在明确定义的算法点被调用。Visitor 函数在Visitor Concepts章节有详细说明。BGL 为通常的任务提供了几种visitor，包括记录前驱节点的visitor.作为扩充BGL的一种方法鼓励用户写自己的visitor.这里我们将迅速浏览实现和使用前驱记录 ， 由于我们使用dijkstra_shortest_paths()算法，所以我们创建的visitor也必须是一个Dijkstra Visitor.

  record_predecessors visitor 的泛函性分成两部分。我们使用一个property map来存储和访问前驱属性。前驱 visitor 只负责记录前驱节点。为了实现这些，我们创建一个使用模版参数的record_predecessors类。由于这个visitor将在一个visitor方法中被填充，我们从一个提供空方法的dijkstra_visitor类继承。predecessor_recorder 类的构造函数将接受一个property map 对象，并把他保存在数据成员中。
template
class record_predecessors : public dijkstra_visitor<>
{
public:
record_predecessors(PredecessorMap p)
: m_predecessor(p) { }

template
void edge_relaxed(Edge e, Graph& g) {
// set the parent of the target(e) to source(e)
put(m_predecessor, target(e, g), source(e, g));
}
protected:
PredecessorMap m_predecessor;
};
  记录前驱节点的工作十分简单，当Dijkstra's algorithm算法释放一个边的时候（添加他到最短路径树中） 我们记录源顶点作为目标顶点的前驱。稍后，如果边再次释放前驱属性将被新的前驱重写，这里我们使用put() 函数在property map中记录前驱。Visitor的edge_filter将告诉算法什么时候调用explore()方法。我们希望边在最短路径树中被通知，所以我们指定tree_edge_tag标记

  最后，我们创建一个辅助函数来更方便的创建predecessor visitors，所有的BGL visitor 都有一个类似的辅助函数。
template record_predecessors
make_predecessor_recorder(PredecessorMap p)
{
    return record_predecessors(p);
}
现在我们准备在Dijkstra's 算法中使用record_predecessors。BGL 的Dijkstra's 算法配备了一个vistitors句柄，所以我们只需要传入我们新的visitor即可。 在这个例子中我们只需要使用1个visitor，尽管BGL在算法中配置了多visitors句柄参数？？(参见Visitor Concepts章).
using std::vector;
using std::cout;
using std::endl;
vector p(num_vertices(G)); //the predecessor 数组
dijkstra_shortest_paths(G, s, distance_map(&d[0]).
visitor(make_predecessor_recorder(&p[0])));

cout << "parents in the tree of shortest paths:" << endl;
for(vi = vertices(G).first; vi != vertices(G).second; ++vi) {
cout << "parent(" << *vi;
if (p[*vi] == Vertex())
cout << ") = no parent" << endl;
else
cout << ") = " << p[*vi] << endl;
}
输出结果:
parents in the tree of shortest paths:
parent(0) = no parent
parent(1) = 4
parent(2) = 0
parent(3) = 2
parent(4) = 3

注意:
新版本Dijkstra's algorithm包括了一个用来记录前驱的指定参数，所以前驱visitor 并不需要。但上面仍不失为一个好的例子。