基于α-β剪枝算法的智能五子棋

一、基本介绍

 

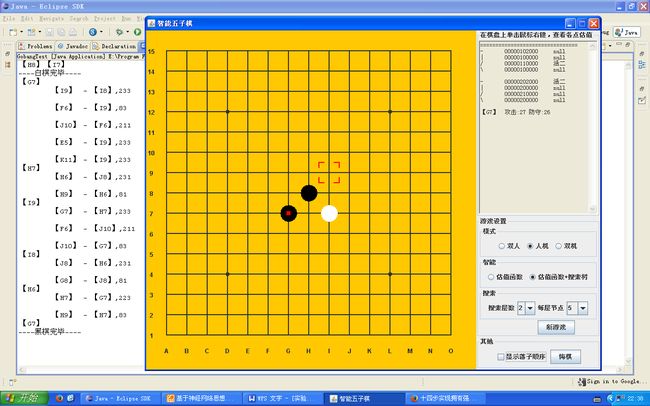
游戏界面：使用了Java Swing进行开发，如图所示。

 

 

游戏步骤：

1. 先设置游戏的参数，可以选择模式（双人、单人、双机），智能（估值函数、估值函数+搜索树），搜索树（层数、每层节点），再开始游戏；

2. 在棋盘上单击鼠标左键，落下棋子；

3. 在棋盘上单击鼠标右键，查看该点的估值；

4. 可以显示落子顺序和悔棋；

5. 使用搜索树AI时，控制台显示搜索过程；

6. 某方胜利后，游戏结束。

 

 

二、棋型确定

 

问题：

1．五子棋棋型的定义十分模糊，如网上对活二、眠三、死四的定义经常自相矛盾。

2．在大部分论文中，考虑的棋型非常少，如对活三的典型棋型列举不够完整，且常把眠三当死三。

 

正确、完全的棋型：

以上问题，令我奔溃了很久，最后对比了N个文献，才确定了比较可信的参考，棋型整理如下：

棋型	定义	表达式 （1黑，2白，0空）	图例（来自五子棋贴吧）
长连	至少五颗同色棋子连在一起	11111
活四	有两个连五点（即有两个点可以形成五），图中白点即为连五点	011110
冲四	有一个连五点	011112 0101110 0110110
活三	可以形成活四的三	01110 010110
眠三	只能够形成冲四的三	001112 010112 011012 10011 10101 2011102
活二	能够形成活三的二	00110 01010 010010
眠二	能够形成眠三的二	000112 001012 010012 10001 2010102 2011002	（图不全）
死四	两头都被封堵的四	211112	（图缺）
死三	两头都被封堵的三	21112	（图缺）
死二	两头都被封堵的二	2112	（图缺）

 

 

棋型判断：

由于棋型比较多，判断起来不太有规律。我就直接取出某点的横、竖、撇、捺四个方向的字串，用正则表达式判断棋型了，这样的效率应该还不错。

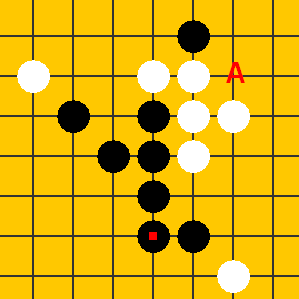
例如对下图A点，如果放白子，可以在横向形成“20022200000”活三，如果放黑子，可以在捺向形成“00001100000”活二。

     

 

 

 

三、落子估值方式

 

分析：棋子落在哪里最好？

1. 需要考虑落下后会在四个方向各形成什么棋型，是否形成组合棋型，然后进行初步打分；

2. 同时还要考虑落子位置，一般同分情况下越中心的点越好；

3. 可以分析对攻击效果、防守效果、综合效果。

 

初步打分：

就是按照威胁程度给每种棋型打分，在理解棋型后，试验了多组估分方式，最后确定效果最好的一组打分方式如下：

棋型（含组合棋型）	分值
长连	100000
活4、双冲4、冲4活3	10000
双活3	5000
活3眠3	1000
眠4	500
活3	200
双活2	100
眠3	50
活2眠2	10
活2	5
眠2	3
死4	-5
死3	-5
死2	-5

 

再统计在四个方向各形成什么棋型，是否形成组合棋型，取最高分为初步打分的结果。

 

落子位置：

根据棋盘分布问题，越中心的点分值应当越高。

private static int[][] position = {

{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },

{ 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0 },

{ 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0 },

{ 0, 1, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 4, 4, 4, 4, 4, 4, 4, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 4, 5, 5, 5, 5, 5, 4, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 4, 5, 6, 6, 6, 5, 4, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 4, 5, 6, 6, 6, 5, 4, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 4, 5, 5, 5, 5, 5, 4, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 4, 4, 4, 4, 4, 4, 4, 3, 2, 1, 0 },

{ 0, 1, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 1, 0 },

{ 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0 },

{ 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0 },

{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } };

 

例如，对下图A点，如果放白子，在四个方向分别会形成活3、活2、眠2，形成两种棋型（组合棋型）活3和活2眠2，最高分为活3对应的200分，再加上位置分值6分，就是206分；如果放黑子，同理是25分。因此，当要在J9落下白子时，可获得攻击分206，防守分25，综合分231。

     

 

 

 

四、棋局估值函数

 

函数描述：

有了落子估值方式后，可以针对某一棋局，分析一定棋盘范围内的各个可落子点的落子估值，将最大综合分作为该棋局的估值。

 

简单智能:

利用估值函数，即可实现简单智能，即只考虑当前局面下的最佳落子点，并落子。

例如，人机对战：

 

优点是速度快，眼前胜利绝不放过，缺点也是显而易见的，对于埋伏了多步的杀法，这种只顾“近忧”的智能无能为力。因此，就需要搜索算法增加“远虑”。

 

 

 

五、搜索算法

 

极大极小搜索：

分析：要想得更远的，棋子落在哪里最好？

1. 在对弈中，可利用棋局估值函数对任何一个局面进行估值，估值越大表明对当前玩家越有利，估分越小则表明越不利；

2. 选择落子时，要考虑对自己第一步越有利的，对对手下一步越不利的，对自己第二步越有利的，以此类推；

3. 这样选择落子时就表现为一棵极大极小搜索树，逐层搜索，对自己轮的层就选最大值的局面，对对手轮就选最小值的局面，直到一定深度。

 

但测试后发现该算法速度比较慢，对15×15的棋盘，搜索第一层有15×15=225个结点，第二层就约有15×15×15×15=50625个节点，完全是指数爆炸。

 

 

α-β剪枝算法:

在搜索的过程中，实际上有搜索很多点是多余的。经过α-β剪枝，可以极大的减少搜索的数量。在查阅资料的过程中，发现α-β剪枝算法是一个基础而经典的算法，还有很多风格、很多变式，值得深入学习。

 

伪代码（建立在MinMax算法基础上）：

alpha-beta(player,board,alpha,beta)

    if(game over in current board position)

        return winner

    children = all legal moves for player from this board

    if(max's turn)

        for each child

            score = alpha-beta(other player,child,alpha,beta)

            (we have found a better best move....)

           if score > alpha then alpha = score           (cut off...)

            if alpha >= beta then return alpha

        return alpha (this is our best move)

    else (min's turn)

        for each child

            score = alpha-beta(other player,child,alpha,beta)

            (opponent has found a better worse move.....)

            if score < beta then beta = score

            (cut off....)

            if alpha >= beta then return beta

        return beta (this is the opponent's best move)

 

以上述伪代码为原型，我尝试实现五子棋AI的α-β剪枝算法。但是试验后发现该原型还有很多不足，比如速率仍然不快，尤其是开局落子时，比如经常忽视近层的绝杀，还需根据五子棋的特点继续优化算法。

 

 

 

六、算法优化

 

速率提高：

1. 限制落子范围：在当前棋局的所有棋子的最左、最右、最上、最下点的5格之内，不超过棋盘边界。这样在棋子较少的时候，搜索结点的数量大大减少。

2. 减少每层的搜索结点：在一方落子后，程序自动对新棋局下的可落子点进行落子估值，保存估值前几名的落子点，在拓展搜索树时，只考虑这些落子点作为新层结点，并进行下一步搜索，大大减少搜索范围。

 

近层绝杀：

在递归过程中，如果发现某落子后可能形成活4、双冲4、冲4活3这些对方无法防守的棋局，则将该落子点的估分人为设成一个无穷大值，即优先这种走法。同时，如果己方和对方同时出现活4、双冲4、冲4活3的棋局，则以己方的攻击为先。

 

综上，最后的α-β算法代码如下（更多详细内容，可见源代码的注解）：

 

public int alpha_beta(int depth, Board board, int alpha, int beta) {

if (depth == level || board.isGameOver() != 0) {

Chess[] sorted = board.getSorted();

Chess move = board.getData()[sorted[0].x][sorted[0].y];

return move.getSum();// 局面估分

}

Board temp = new Board(board);

Chess[] sorted = temp.getSorted();

int score;

for (int i = 0; i < node; i++) {

int x = sorted[i].x;

int y = sorted[i].y;

if (!temp.putChess(x, y))

continue;

if (sorted[i].getOffense() >= Board.Level.ALIVE_4.score) {

score = INFINITY + 1;

} else if (sorted[i].getDefence() >= Board.Level.ALIVE_4.score) {

score = INFINITY;

} else {

score = alpha_beta(depth + 1, temp, alpha, beta);

}

temp = new Board(board);

if (depth % 2 == 0) {// MAX

if (score > alpha) {

alpha = score;

if (depth == 0) {

movex = x;

movey = y;

}

}

if (alpha >= beta)

return alpha;

} else {// MIN

if (score < beta)

beta = score;

if (alpha >= beta)

return beta;

}

}

return depth%2==0?alpha:beta;

}

 

 

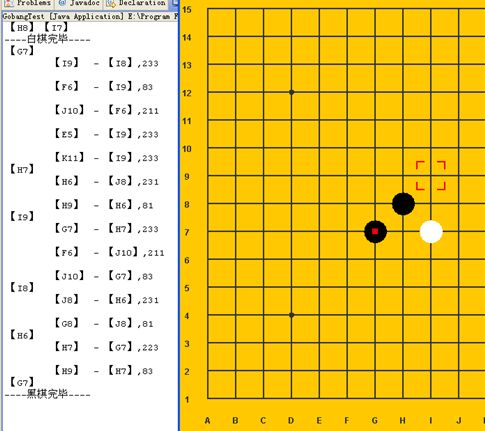
例如，深度为2，每层5个结点，H8黑、I7白后考虑落下黑子，依次拓展落子估值前5大的点G7、H7、I9、I8、H6，根据深度优先搜索，先假设落下G7黑，则再次拓展5个结点I9、F6、J10、E5、K11，其中落子I9白（即共四子）后的棋局（I8是该棋局的最大落子估值点）估值为233，以此类推。根据剪枝原理，最后可得最佳落子点。

 

 

 

 

更多优化的思考：

1. 考虑利用多线程，让算法实现并行计算，每个线程负责不同子树，可提高速率；

2. 落子的影响范围有限，搜索过程中很多点的估值并没有改变，可以考虑把一些点的估值记录下来，以后只要遇到搜索到的节点，就可以直接得到结果，可提高速率；

3. 由于算法的固定性，所以一担玩家一次获胜，按照相同的走法，必然会再次获胜。但除了必杀招或者必防招，一个局面很多时候没有绝对最好的走法，而是有一些都不错的走法。考虑把这些评分差不多走法汇集起来，然后随机选择它们中的一种走法，避免走法的固定。

4. 可利用神经网络思想来提高速率，存储结点信息，增加学习功能，避免再次犯错。

 

 

七、结语

 

感悟：

花了约一周的时间，网上并没有满意的源码参考来作为基础，基本都是自己完成的，挺有成就感，但是也误了时间，非常抱歉！

整个过程中有几个坎，一是资料混乱，棋型很难确定，二是得弄清楚落子估值和棋局估值函数的联系和区别，这个没有找到明确描述的资料，是我自己分析猜测的，三是写完α-β算法不是万事大吉，要做个高智商的AI还很有欠缺。

 

参考：

（界面设计）

http://slab.sinaapp.com/gomoku/

（基本棋型、专业术语）

http://www.rifchina.com/Article/ShowArticle.asp?ArticleID=1038

http://www.rifchina.com/Article/ShowArticle.asp?ArticleID=1038

（α-β剪枝算法）

http://www.cnblogs.com/Blog_SivenZhang/archive/2010/06/13/1757677.html

http://www.cnblogs.com/speeding/archive/2012/09/20/2694704.html

http://blog.csdn.net/allenlsy/article/details/5324441

http://www.xqbase.com/computer/stepbystep3.htm

http://blog.sina.com.cn/s/blog_5d9ee55e0100uuy2.html

（相关论文）

唐永强,汪波.基于神经网络思想及α-β方法的五子棋算法设计.《电脑应用技术》二零零九总第七十二期

简越.基于UML的五子棋人机对弈.本科毕业论文