FFT C语言 修改了matlab
目录
- FFT修改
- FFT-dit的算法讨论
- 程序
- c结果:
- matlab的程序结果:
- 修改了,matlab的程序
FFT修改
FFT-dit的算法讨论
级的概念
M = l o g 2 N M=log_2N M=log2N,所以N点DFT可分成M级。
下图为8点FFT时间抽取算法信号流程图,方框分别为m=0,m=1,m=2;
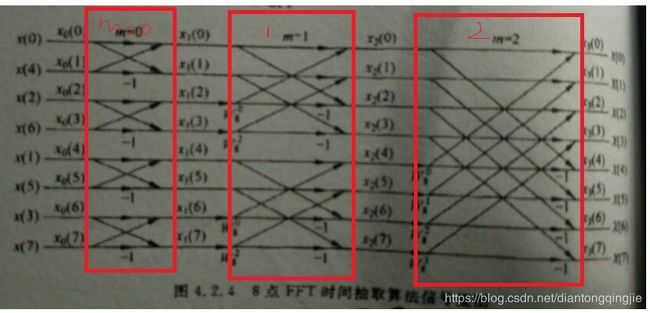
码位倒置
交换后输出序列x(k)依照正序排列,但输入序列x(n)的次序不再是原来的自然次序,这是由于将x(n)按奇,偶分开产生的。
雷德算法: 对于自然顺序(二进制)我们是在低位加 1 得到下一位数,对于倒位序我们是在高位加 1 向低位进位。比如已知一个倒位序数是J求其下一个倒位序数,N位总数 ,把J与N/2比较若J
参考:https://blog.csdn.net/corcplusplusorjava/article/details/17119567
Rader参考程序:
#include
#include
#include
int main(void)
{
int array[8]={0,1,2,3,4,5,6,7};
int i,j,k;
int N = 8;
int temp;
j = 0;
for(i = 0; i < N -1; i ++)
{
if(i < j)
{
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
k = N >> 1;
while( k <= j)
{
j = j - k;
k >>= 1;
}
j = j + k;
}
for( i = 0; i < N; i ++)
printf("%d %d\n",i,array[i]);
printf("\n");
return 0;
}
结果:
W r W^r Wr因子的分布
规律:第m级, W 2 m + 1 r W_{2^{m+1}}^r W2m+1r
在fft中,乘法主要来自旋转因子。因为 W r = c o s ( 2 π r N ) − j s i n ( 2 π r N ) , 所 以 在 对 W r W^r=cos(\frac{2{\pi}r}{N})-jsin(\frac{2{\pi}r}{N}),所以在对W^r Wr=cos(N2πr)−jsin(N2πr),所以在对Wr相乘时,必须产生相应的正,余弦函数。编程时,产生正,余弦函数两个方法,一个是在每一步直接产生,二是在程序开始前预先计算W^r存于一个数组中,等效一个正,余弦函数的“表”。
蝶形单元
第m级,有
X m + 1 ( p ) = x m ( p ) + W N r X m ( q ) X_{m+1}(p)=x_{m}(p)+W_N^{r}X_m(q) Xm+1(p)=xm(p)+WNrXm(q)
X m + 1 ( q ) = x m ( p ) − W N r X m ( q ) X_{m+1}(q)=x_{m}(p)-W_N^{r}X_m(q) Xm+1(q)=xm(p)−WNrXm(q)
"组"的概念
每一级的N/2个蝶形单元可以分成若干组,每一组有着相同的结构及W^r因子分布。
第m级的组数是 N / 2 m + 1 N/2^{m+1} N/2m+1.
程序
A.1< B.FFT蝶形算法使用三重循环,下一层的数据都是由上一层计算得到的。 对比结果还是有差异。 FFT过程中,对C理解还不够,对蝶形运算算法还不理解,对三重循环还不熟悉 。#include c结果:
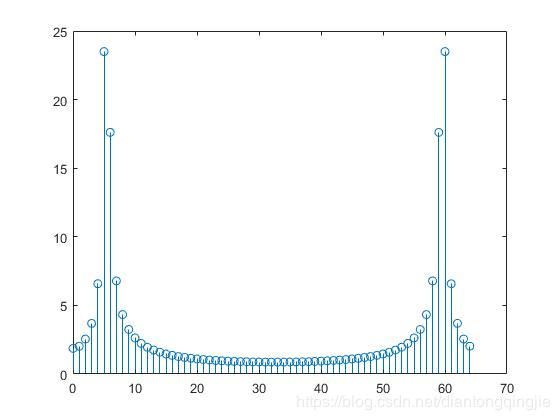
matlab的程序结果:
N=64;
n=0:1:N;
x=cos(n*pi/6);
X=fft(x);
figure
stem(n,abs(X))
修改了,matlab的程序
>> n=0:1:63;
>> x=cos(n*pi/6);
>> y=fft(x);
>> figure
>> stem(n,abs(y))