语音幅度统计-matlab-有问题

语音信号的统计特性

幅度分布的概率密度

归一化：均值为0，方差为1.

可实现归一化的matlab函数 zscore: z-score 标准化(正太标准化)是基于原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。将A的原始值x使用z-score标准化到x’。

（matlab的归一化函数为mapminmax，此处以A=[100 200 300 400 500]为例，使用mapminmax函数进行归一化，调用格式为[A1,PS]=mapminmax(A)。A1为归一化后的数值。PS是一种对应关系，包含数据的最大值最小值等，如下图所示。归一化函数的对应关系为y=(ymax-ymin)*(x-xmin)/(xmax-xmin)+ymin。此处以200验证某一个元素的值，那么y=2*(200-100)/(500-100)+(-1)=-1/2=-0.5）

均值 mean

方差 var

标准差 std

幅度分布

${\alpha }_X$是语音信号的标准差

x是语音信号的幅度

1.修正伽玛（Gamma)概率密度
$$P_G(x)=\frac{\sqrt{k}}{2\sqrt{\pi }}\cdot \frac{e^{-k|x|}}{\sqrt{|x|}}$$

$$k=\frac{\sqrt{3}}{2{\alpha }_X}$$

2.拉普拉斯（Laplacian）分布
$$P_L(x)=0.5\alpha e^{-\alpha |x|}$$
$\alpha $是语音信号的标准差$\alpha_x$决定的常数
$$\alpha =\frac{\sqrt{2}}{{\sigma }_x}$$
3.高斯密度分布
$$P_g(x)=\frac{1}{\sqrt{2\pi }{\sigma }_x}exp(-\frac{x^2}{2{\sigma }_x^2})$$
x是语音信号的幅度，${\alpha }_x$是语音信号的标准差

matlab

画出语音信号的幅度概率密度图

1.画出直方图

用函数hist()可以得出每个区间的频数

[n,x]=hist(data1,100);%计算小区间内的频数及区间中点值

2.在画出幅度概率密度函数图

用每个区间的频数除以数据，可以得出每个区间的频率

3.matlab代码

close all;
clear;
clc;
[data1,fs]=audioread('soo2.wav');
data=abs(data1);
% %histogram(data1);
 hold on
% u=mean(data);%均值
% v=std(data);%标准差
% h=max(data)-min(data);%极差
% d=0.01;%根据直方图，得到每个区间的长度为0.1
 [n,x]=hist(data1,100);%计算小区间内的频数及区间中点值
% hold on
% plot(x,n);
% hold on
% % xlabel('每个区间中点值');
subplot(211)
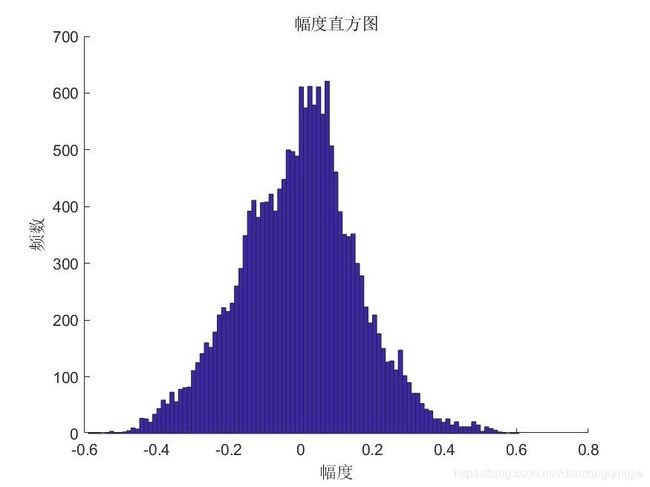
 hist(data1,100)%画出直方图，
 xlabel('幅度');
ylabel('频数');
 title('幅度直方图');
 hold on
% ylabel('频数');
%  n为每个区间内的频数
%f=data/length(data);%计算频率
%f1=f/d;%频率除以分割区间的长度
% x1=min(data):0.01:max(data);
% y=normpdf(x1,u,v);
% plot(x1,y,'r','linewidth',2);
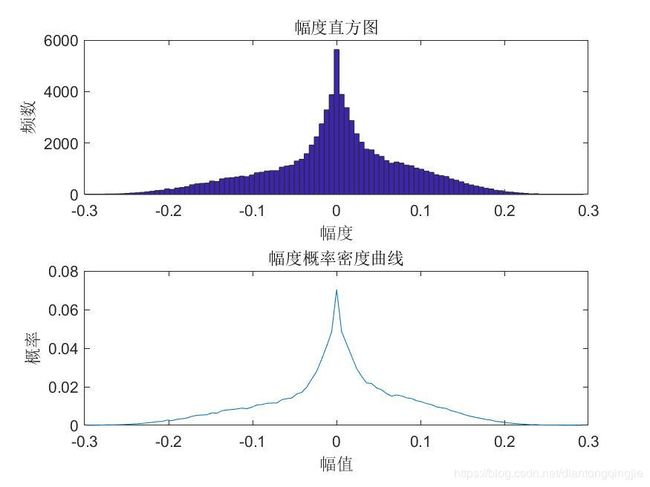
subplot(212)
fi=n/sum(n);
plot( x,fi);
xlabel('幅值');
ylabel('概率');
title('幅度概率密度曲线');
hold on

4.导入不同的类型的音频对比

man

women

music

speak

带入其他概率密度曲线对比

只导入语音信号（即只有讲话的声音speak.wav）

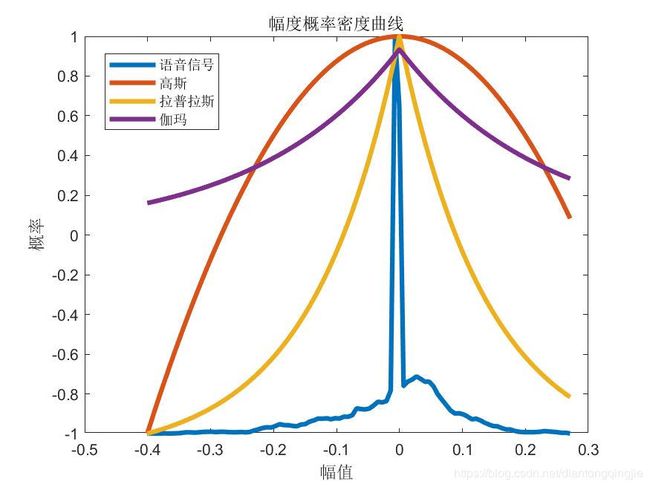
分别用高斯，拉普拉斯，伽玛带入对比。

没法把数据归一化为均值为0，方差为1的数据。

都是字均值为0的附近，方差为1的附近。

man

musci

women

speak

完全说话-普通话标准考试说话

对比起来，拉普拉斯好像好点

代码：

clear;
clc
[data1,fs]=audioread('man.wav');
[n,x]=hist(data1,100);%计算小区间内的频数及区间中点值
v=std(x);%标准差
j=abs(x);%绝对值
fi=n/sum(n);
y=mapminmax(fi);
plot( x,y,'linewidth',3);
xlabel('幅值');
ylabel('概率');
title('幅度概率密度曲线');
hold on
%gasi
gs=(1/sqrt(2pi)v)exp(-1x.^2/2v^2);
g=mapminmax(gs);
plot(x,g,'linewidth',3);
hold on
%la
a=sqrt(2)/v;%公式
pl=0.5aexp(-aj);%公式
p2=zscore(pl);
plot(x,p2,'linewidth',3);
%gama
j=j';
k=sqrt(3)/(2v);
gm1=sqrt(k)/(2sqrt(pi));
gm2=exp(-kj)/sqrt(j);
gm=gm1gm2;
gam=zscore(gm);
plot(x,gm(:,1),'linewidth',3);
%这里因为计算时j只被当成一个数，算出来的gm2为一个数
%转制了j，使得为一列数据
%得出的结果只取第一列,函数为a(:,1)
%man.wav,数据为最后一列，即为第一百列
hold on
legend('语音信号','高斯','拉普拉斯','伽玛');

#问题
1.数据太少？
2.乖乖的？