AlignedReID论文学习
AlignedReID论文学习
论文：《AlignedReID: Surpassing Human-Level Performance in Person Re-Identification》
下载链接：https://arxiv.org/abs/1711.08184v1
这篇论文将局部特征对齐引入到行人重识别的任务中，结合局部特征和全局特征计算损失函数，得到了非常好的结果（据说超越人类识别水平！！！）
需要提前掌握的知识点：
- 度量学习（Metric Learning）
- 特征对齐（Feature Alignments）
- 交互学习（Mutual Learning）
- 重排（Re-Ranking）
AlignedReID 框架
直接上图：
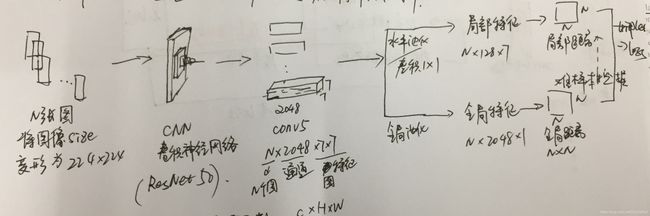
首先 N 张图进入到卷积神经网络（ResNet50），得到 2048 × \times × 7 × \times × 7 的特征图，此时开始分化：特征图经过全局池化得到 2048 × \times × 1 的全局特征（图中下面一路）；特征图经过水平池化+ 1 × \times × 1 的卷积层后得到 128 × \times × 7 的局部特征（图中上面一路），这里 1 × \times × 1 的卷积层是为了改变输出特征的通道数。
距离计算：
全局特征：L2距离
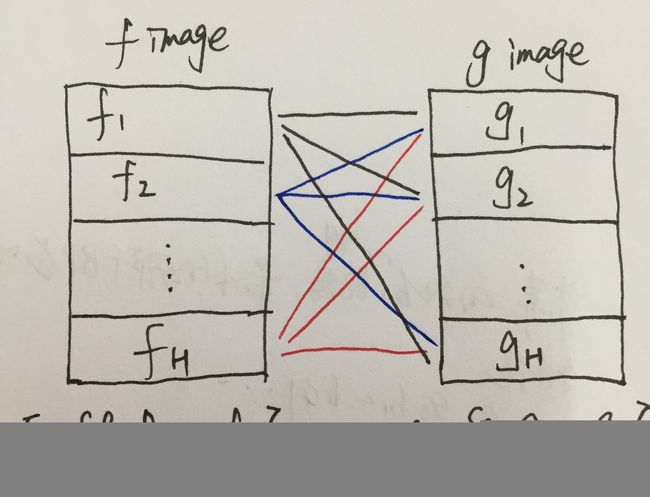
局部特征：对两个特征图在水平方向上进行划分，然后通过从顶部到底部的搜索方法来进行特征匹配，如下图所示：
即第一张图像的第 i i i 个垂直部分与第二张图像的第 j j j 个垂直部分之间的距离 d i , j d_{i, j} di,j 计算为：
d i , j = e ∥ f i − g j ∥ 2 − 1 e ∥ f i − g j ∥ 2 + 1 i , j ∈ 1 , 2 , 3 … , H d_{i, j}=\frac{e^{\left\|f_{i}-g_{j}\right\|_{2}}-1}{e^{\left\|f_{i}-g_{j}\right\|_{2}}+1} \quad i, j \in 1,2,3 \ldots, H di,j=e∥fi−gj∥2+1e∥fi−gj∥2−1i,j∈1,2,3…,H
两个图像的距离矩阵 D D D 为：
D = [ d 1 , 1 d 2 , 1 ⋯ d H , 1 d 1 , 2 d 2 , 2 ⋯ d H , 2 ⋮ ⋮ ⋱ ⋮ d 1 , H d 2 , H ⋯ d H , H ] H × H D=\left[ \begin{array}{cccc}{d_{1,1}} & {d_{2,1}} & {\cdots} & {d_{H, 1}} \\ {d_{1,2}} & {d_{2,2}} & {\cdots} & {d_{H, 2}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {d_{1, H}} & {d_{2, H}} & {\cdots} & {d_{H, H}}\end{array}\right]_{H \times H} D=⎣⎢⎢⎢⎡d1,1d1,2⋮d1,Hd2,1d2,2⋮d2,H⋯⋯⋱⋯dH,1dH,2⋮dH,H⎦⎥⎥⎥⎤H×H
局部特征距离即为矩阵 D D D中从（1，1）到（H，H）的最短总距离 S S S， S S S由动态规划方法计算。
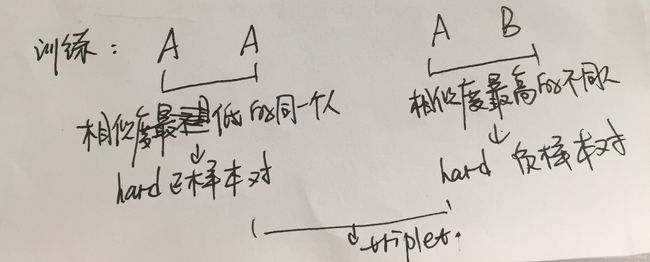
在训练阶段采用TriHard loss 作为度量学习的loss：
交互学习
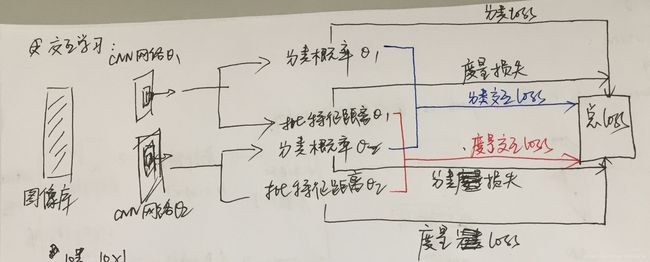
交互学习的框架如下图所示：
- 度量loss：由全局和局部距离决定；
- 分类交互loss：由分类的KL差异指标决定；
- 度量交互loss：仅由全局距离决定。