神经网络训练的一些建议（方差和偏差的问题：正则化）

参数和超参数

算法中的learning rate a（学习率）、iterations(梯度下降法循环的数量)、L（隐藏层数目）、n（隐藏层单元数目）、choice of activation function（激活函数的选择）都需要你来设置，这些数字实际上控制了最后的参数W和b的值，所以它们被称作超参数。

实际上深度学习有很多不同的超参数，之后我们也会介绍一些其他的超参数，如momentum、mini batch size、regularization parameters等等

超参数需要人为设定的，参数是模型训练的，所以超参数的设定对神经网络的训练是很重要的。

训练，验证，测试集（Train / Dev / Test sets）

划分原则
在机器学习发展的小数据量时代，常见做法是将所有数据三七分，就是人们常说的70%验证集，30%测试集，如果没有明确设置验证集，也可以按照60%训练，20%验证和20%测试集来划分。这是前几年机器学习领域普遍认可的最好的实践方法。
如果只有100条，1000条或者1万条数据，那么上述比例划分是非常合理的。

数据集规模较大的，验证集和测试集要小于数据总量的20%或10%。

要确保验证集和测试集的数据来自同一分布。

偏差和方差

（主要看图，一目了然）
假设这就是数据集，如果给这个数据集拟合一条直线，可能得到一个逻辑回归拟合，但它并不能很好地拟合该数据，这是高偏差（high bias）的情况，我们称为“欠拟合”（underfitting）。
相反的如果我们拟合一个非常复杂的分类器，比如深度神经网络或含有隐藏单元的神经网络，可能就非常适用于这个数据集，但是这看起来也不是一种很好的拟合方式分类器方差较高（high variance），数据过度拟合（overfitting）。
在两者之间，可能还有一些像图中这样的，复杂程度适中，数据拟合适度的分类器，这个数据拟合看起来更加合理，我们称之为“适度拟合”（just right）是介于过度拟合和欠拟合中间的一类。

几个方差和偏差的例子（如果需要快速了解可以略过）
假设训练集误差是15%，我们把训练集误差写在首行，验证集误差是16%，假设该案例中人的错误率几乎为0%，人们浏览这些图片，分辨出是不是猫。算法并没有在训练集中得到很好训练，如果训练数据的拟合度不高，就是数据欠拟合，就可以说这种算法偏差比较高。相反，它对于验证集产生的结果却是合理的，验证集中的错误率只比训练集的多了1%，所以这种算法偏差高，因为它甚至不能拟合训练集，这与上一张幻灯片最左边的图片相似。
再举一个例子，训练集误差是15%，偏差相当高，但是，验证集的评估结果更糟糕，错误率达到30%，在这种情况下，我会认为这种算法偏差高，因为它在训练集上结果不理想，而且方差也很高，这是方差偏差都很糟糕的情况。
再看最后一个例子，训练集误差是0.5%，验证集误差是1%，用户看到这样的结果会很开心，猫咪分类器只有1%的错误率，偏差和方差都很低。

为什么要关注方差和偏差

当我们训练一个神经网络，我们需要知道这个算法偏差高不高
如果偏差较高，典型的欠拟合状态，试着评估训练集或训练数据的性能。如果偏差的确很高，甚至无法拟合训练集，那么你要做的就是选择一个新的网络，比如含有更多隐藏层或者隐藏单元的网络，或者花费更多时间来训练网络，或者尝试更先进的优化算法

评估方差主要看验证集的性能
如果方差高，最好的解决办法就是采用更多数据，如果你能做到，会有一定的帮助，但有时候，我们无法获得更多数据，我们也可以尝试通过正则化来减少过拟合

解决高方差的方法

深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。

正则化

如果用的是L1正则化，w最终会是稀疏的，也就是说w向量中有很多0，有人说这样有利于压缩模型，因为集合中参数均为0，存储模型所占用的内存更少。实际上，虽然L1正则化使模型变得稀疏，却没有降低太多存储内存，所以我认为这并不是L1正则化的目的，至少不是为了压缩模型，人们在训练网络时，越来越倾向于使用L2正则化，L2正则化也被称为“权重衰减”。

正则化为什么能解决过拟合

直觉上，L2的超参数设置的比较大，会让很多神经元的权值接近零，消除很多神经元的影响，使整个网络变得简单，减少过拟合，如下图所示，超参数的大小调节有一个过渡的状态，从右到左。

dropout正则化

除了L2正则化，还有一个非常实用的正则化方法——“Dropout（随机失活）”，我们来看看它的工作原理。

假设你在训练上图这样的神经网络，它存在过拟合，这就是dropout所要处理的，我们复制这个神经网络，dropout会遍历网络的每一层，并设置消除神经网络中节点的概率。假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率都是0.5，设置完节点概率，我们会消除一些节点，然后删除掉从该节点进出的连线，最后得到一个节点更少，规模更小的网络，然后用backprop方法进行训练。

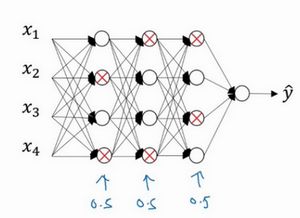
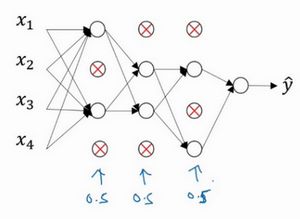
这是网络节点精简后的一个样本，对于其它样本，我们照旧以抛硬币的方式设置概率，保留一类节点集合，删除其它类型的节点集合。对于每个训练样本，我们都将采用一个精简后神经网络来训练它，这种方法似乎有点怪，单纯遍历节点，编码也是随机的，可它真的有效。不过可想而知，我们针对每个训练样本训练规模极小的网络，最后你可能会认识到为什么要正则化网络，因为我们在训练极小的网络。

注意：drop掉的神经元都需要备份，测试的时候每一个神经元都要与它选中的概率相乘完成相应的还原。
在图像领域应用很多，其他领域可能并不是那么适用

early stopping

在训练过程中，我们希望训练误差，代价函数J都在下降，通过early stopping，我们不但可以绘制上面这些内容，还可以绘制验证集误差，它可以是验证集上的分类误差，或验证集上的代价函数，逻辑损失和对数损失等，你会发现，验证集误差通常会先呈下降趋势，然后在某个节点处开始上升，early stopping的作用是，你会说，神经网络已经在这个迭代过程中表现得很好了，我们在此停止训练吧，得到验证集误差