R语言使用层次聚类处理数据

凝聚层次聚类说明

层次聚类可以分成凝聚（agglomerative,自底向上）和分裂（divisive，自顶向下）两种方法来构建聚类层次，但不管采用那种算法，算法都需要距离的相似性度量来判断对数据究竟是采取合并还是分裂处理。

凝聚层次聚类操作

采用层次聚类，将客户数据集分成不同的组，从github上下载数据：
https://github.com/ywchiu/ml_R_cookbook/tree/master/CH9下载
customer.csv文件

customer = read.csv("d:/R-TT/example/customer.csv")
head(customer,10)
   ID Visit.Time Average.Expense Sex Age
1   1          3             5.7   0  10
2   2          5            14.5   0  27
3   3         16            33.5   0  32
4   4          5            15.9   0  30
5   5         16            24.9   0  23
6   6          3            12.0   0  15
7   7         12            28.5   0  33
8   8         14            18.8   0  27
9   9          6            23.8   0  16
10 10          3             5.3   0  11

检查数据集结构：

str(customer)
'data.frame':   60 obs. of  5 variables:
 $ ID             : int  1 2 3 4 5 6 7 8 9 10 ...
 $ Visit.Time     : int  3 5 16 5 16 3 12 14 6 3 ...
 $ Average.Expense: num  5.7 14.5 33.5 15.9 24.9 12 28.5 18.8 23.8 5.3 ...
 $ Sex            : int  0 0 0 0 0 0 0 0 0 0 ...
 $ Age            : int  10 27 32 30 23 15 33 27 16 11 ...

对客户数据进行归一化处理：
数据标准化（归一化）处理是数据挖掘的一项基础工作，不同评价指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。以下是两种常用的归一化方法：
一、min-max标准化（Min-Max Normalization）
也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0 - 1]之间。转换函数如下：

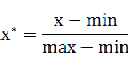
其中max为样本数据的最大值，min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。
二、Z-score标准化方法
这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

其中为所有样本数据的均值，为所有样本数据的标准差。
此处采用方法二

customer = scale(customer[,-1])
customer
       Visit.Time Average.Expense        Sex         Age
 [1,] -1.20219054     -1.35237652 -1.4566845 -1.23134396
 [2,] -0.75693479     -0.30460718 -1.4566845  0.59951732
 [3,]  1.69197187      1.95762206 -1.4566845  1.13800594
 [4,] -0.75693479     -0.13791661 -1.4566845  0.92261049
 [5,]  1.69197187      0.93366567 -1.4566845  0.16872643
 [6,] -1.20219054     -0.60226893 -1.4566845 -0.69285535
 [7,]  0.80146036      1.36229858 -1.4566845  1.24570366
 [8,]  1.24671612      0.20737101 -1.4566845  0.59951732
 [9,] -0.53430691      0.80269450 -1.4566845 -0.58515763
[10,] -1.20219054     -1.40000240 -1.4566845 -1.12364624

使用自底向上的聚类方法处理数据集：

hc = hclust(dist(customer,method = "euclidean"),method = "ward.D2")
> hc

Call:
hclust(d = dist(customer, method = "euclidean"), method = "ward.D2")

Cluster method   : ward.D2 
Distance         : euclidean 
Number of objects: 60 

最后，调用plot函数绘制聚类树图

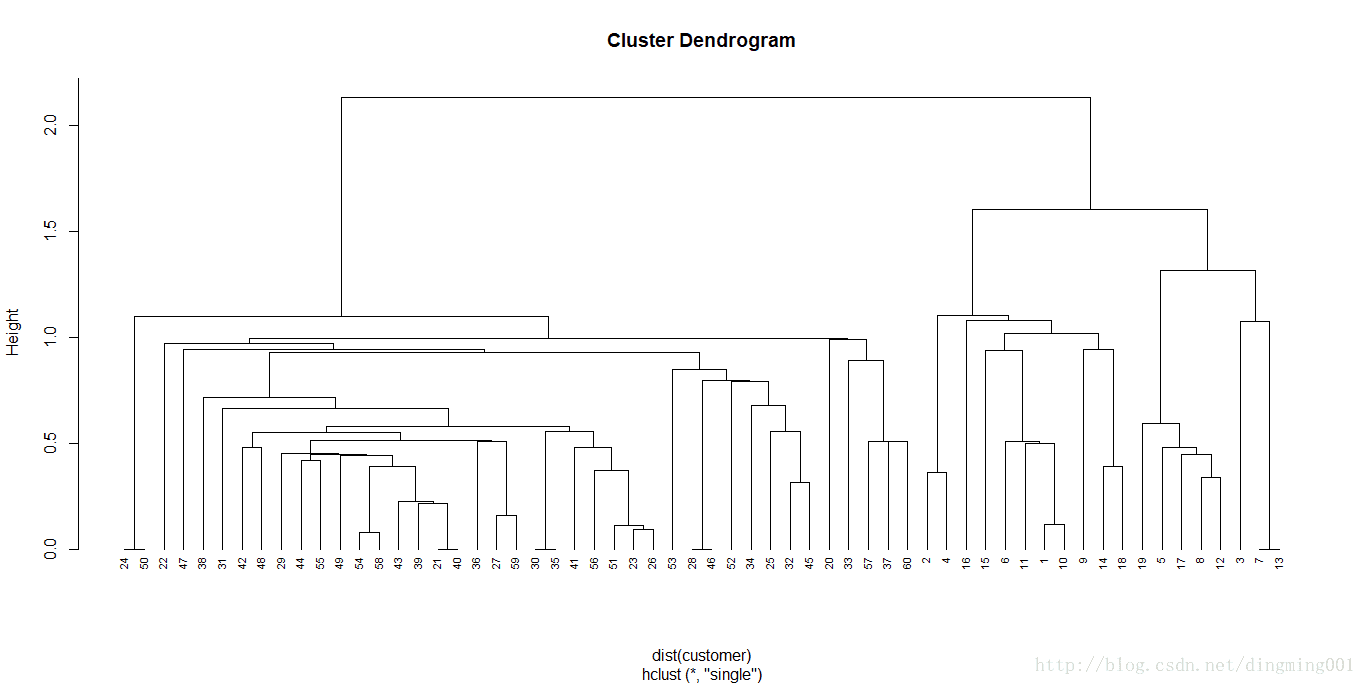
plot(hc,hang = -0.01,cex =0.7)

使用离差平方和绘制聚类树图
还可以使用最短距离法（single）来生成层次聚类并比较以下两者生成的聚类树图的差异：

hc2 = hclust(dist(customer),method = "single")
plot(hc2,hang = -0.01,cex = 0.7)

使用最短距离法绘制聚类树图

凝聚层次聚类原理

层次聚类是一种通过迭代来尝试建立层次聚类的方法，通常可以采用以下两种方式完成：

凝聚层次聚类

这是一个自底向上的聚类方法。算法开始时，每个观测样例都被划分到单独的簇中，算法计算得出每个簇之间的相似度（距离），并将两个相似度最高的簇合成一个簇，然后反复迭代，直到所有的数据都被划分到一个簇中。

分裂层次聚类

这是一种自顶向下的聚类算法，算法开始时，每个观测样例都被划分同一个簇中，然后算法开始将簇分裂成两个相异度最大的小簇，并反复迭代，直到每个观测值属于单独一个簇。

在执行层次聚类操作之前，我们需要确定两个簇之间的相似度到底有多大，通常我们会使用一些距离计算公式：
最短距离法(single linkage），计算每个簇之间的最短距离：
dist(c1,c2) = min dist(a,b)
最长距离法(complete linkage）,计算每个簇中两点之间的最长距离：
dist(c1,c2) = max dist(a,b)
平均距离法（average linkage）,计算每个簇中两点之间的平均距离：
最小方差法（ward）,计算簇中每个点到合并后的簇中心的距离差的平方和。
调用plot函数绘制聚类图，样例的hang值小于0,因此聚类树将从底部显示标签，并使用cex将坐标轴上的标签字体大小缩小为正常的70%，此外，为了比较最小方差法和最短距离法在层次聚类上的差异，我们还绘制了使用最短距离法得到的聚类树图。

分裂层次聚类

调用diana函数执行分裂层次聚类

library(cluster)
dv = diana(customer,metric = "euclidean")

调用summary函数输出模型特征信

summary(dv)

如果想构建水平聚类树

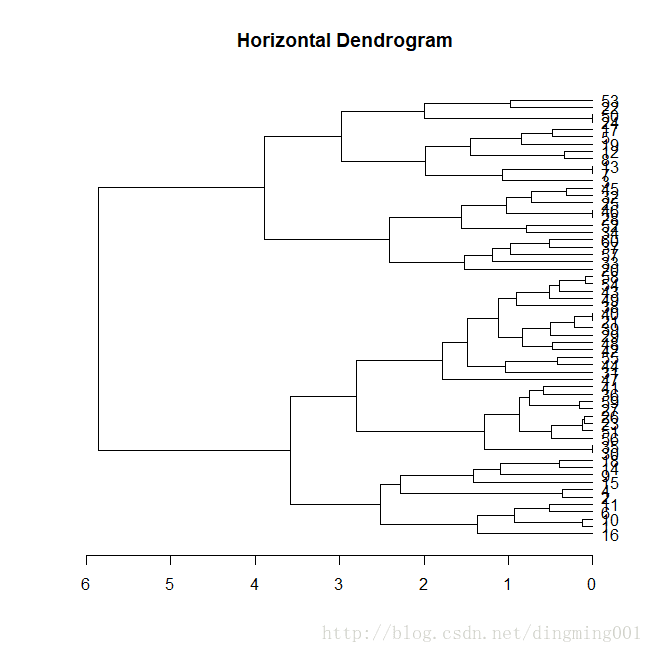
library(magrittr)
dend = customer %>% dist %>% hclust %>% as.dendrogram
dend %>% plot(horiz = TRUE,main = "Horizontal Dendrogram")

水平聚类树