求解强连通分量算法之---Kosaraju算法
本文提纲:
- 问题描述
- Kosaraju 算法
问题描述:
什么是强连通分量(StronglyConnected Component)(或者,被称为强连通子图,Strongly Connected Subgraph)?
首先需要明白的是,强连通分量只可能存在于有向图中,无向图中是不存在强连通分量的,当然,无向图中也有对应物,被称为连通分量(Connected Component),求解无向图中的连通分量,根据具体要求,可以选择使用并查集或者DFS。
看一张取自wiki的图就明白什么是强连通分量了:
以上用虚线围绕的部分就是一个强连通分量,因此上图中总共含有三个。
对于一个强连通分量中的任意一对顶点(u,v),都能够保证分量中存在路径使得u->v,v->u
比如上图中由a,b,e这三个顶点构成的分量中,任意两个顶点间都存在路径可达。
顺便也介绍一下有关“缩点”的概念:
由于强连通分量的特殊性,在一些实际应用中,会将每个强连通分量看成一个点,然后进行处理。这样做主要是为了降低图的复杂度,特别是在强连通分量规模大、数量多的情况中,利用“缩点”能大幅度降低图的复杂度。
缩点后得到的图,必定是DAG。用反正能够很方便的进行证明:因为若图中含有环路,即意味着至少有两个点彼此可达,那么按照强连通分量的定义,这两个点应该属于一个分量中,因而在缩点发生后,会被一个点所代表。由此推导出矛盾。比如,对上图进行缩点处理,最后的结果就是:
设(a,b,c) -> a',(f,g) -> b',(c,d,h) -> c'
因此最后的图就可以表示为:
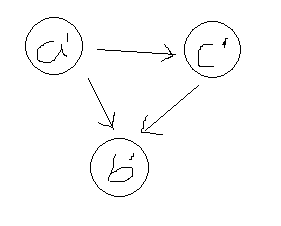
更加具体,更加严谨的表述,可以参考:
http://en.wikipedia.org/wiki/Strongly_connected_component
Kosaraju 算法
首先摘录一段wiki上的算法过程描述:
(取自http://en.wikipedia.org/wiki/Kosaraju%27s_algorithm)
- Let G be a directed graph and S be an empty stack.
- While S does not contain all vertices:
- Choose an arbitrary vertex v not in S. Perform a depth-first search starting at v. Each time that depth-first search finishes expanding a vertex u, push u onto S.
- Reverse the directions of all arcs to obtain the transpose graph.
- While S is nonempty:
- Pop the top vertex v from S. Perform a depth-first search starting at v. The set of visited vertices will give the strongly connected component containing v; record this and remove all these vertices from the graph G and the stack S. Equivalently, breadth-first search (BFS) can be used instead of depth-first search.
仔细观察步骤2-a,可以发现,这个过程和使用基于DFS的拓扑排序中添加顶点到最终结果栈中的过程几乎一致。(请参考这里)只不过这里的图不一定是DAG,而拓扑排序中的图一定是DAG。
在这里顺便提一下在调用dfs的过程中,几种添加顶点到集合的顺序。一共有四种顺序:
- Pre-Order,在递归调用dfs之前将当前顶点添加到queue中
- Reverse Pre-Order,在递归调用dfs之前将当前顶点添加到stack中
- Post-Order,在递归调用dfs之后将当前顶点添加到queue中
- Reverse Post-Order,在递归调用dfs之后将当前顶点添加到stack中
最后一种的用途最广,至少目前看来是这样,比如步骤2-a以及拓扑排序中,都是利用的Reverse Post-Order来获取顶点集合。
对于DAG,利用Reverse Post-Order最终获取的集合就代表对该图进行拓扑排序的结果,但是对于非DAG而言,这样处理之后得到的是一种“伪拓扑排序”结果,为什么这样说,因为最终的结果不一定满足拓扑排序中严格的偏序定义,比如对文中第一幅图进行“伪拓扑排序“后的结果为可能为(结果不唯一,具体可以参考拓扑排序那篇文章中的相关部分):
(a,b,e,c,d,h,g,f)
将结果和原图对比,可以发现,结果不满足偏序关系,因为存在回向边:
e->a,d->c,h->d,f->g
而这些回向边,就是构成强连通分量的关键。为了突出这些回向边,Kosaraju算法的步骤三就是将图进行转置。转置后,原来的回向边就都变成正向边了:
a->e,c->d,d->h,g->f
对转置后的图按照上面”伪拓扑排序“中顶点出现的顺序(a,e,b,c,d,h,g,f)调用DFS,即步骤4。
而每次调用DFS形成的一颗搜索树,就构成了原图中的一个强连通分量。比如调用dfs(a),会调用dfs(e),紧接着后者有调用了dfs(b)。然后依次返回,因此a,b,e就构成了一个强连通分量。依次类推,c,d,h以及g,f也分别构成强连通分量。
回顾一下Kosaraju的主要步骤:
- 对G求解Reverse Post-Order,即上文中的”伪拓扑排序“
- 对G进行转置得到GR
- 按照第一步得到的集合中顶点出现的顺序,对GR调用DFS得到若干颗搜索树
- 每一颗搜索树就代表了一个强连通分量
坦率地说,这个算法的想法很巧妙,为了突出回向边,而对图进行转置,然后对转置的图按照之前得到的顶点序列进行DFS调用。整个算法的确能够正确工作,但是总感觉怪怪的,确实,这个算法不太好理解,尽管它的实现十分简单直观。
使用Java的实现代码:
public class KosarajuSCC {
private Digraph digraph;
private int V;
private boolean[] visited;
private int[] components;
private List> sccs;
// record the current component id
private int current = 0;
// reverseTopo is not necessarily a topological order, it should be reverse
// post order instead
public KosarajuSCC(Digraph digraph, Iterable reverseTopo) {
this.digraph = digraph;
V = digraph.getV();
visited = new boolean[V];
components = new int[V];
for (int v : reverseTopo) {
if (!visited[v]) {
dfs(v);
current++;
}
}
}
private void dfs(int v) {
visited[v] = true;
components[v] = current;
for (int w : digraph.adj(v)) {
if (!visited[w]) {
dfs(w);
}
}
}
public int[] getComponents() {
return components;
}
public List> getSccs() {
sccs = new ArrayList>();
for (int i = 0; i < current; i++) {
sccs.add(new ArrayList());
}
for (int i = 0; i < V; i++) {
sccs.get(components[i]).add(i);
}
return sccs;
}
}
下面对这个算法的正确性进行证明:(如果没有兴趣,可以直接略过 :D)
证明的目标,就是最后一步 --- 每一颗搜索树代表的就是一个强连通分量
证明:设在图GR中,调用DFS(s)能够到达顶点v,那么顶点s和v是强连通的。
两个顶点如果是强连通的,那么彼此之间都有一条路径可达,因为DFS(s)能够达到顶点v,因此从s到v的路径必然存在。现在关键就是需要证明在GR中从v到s也是存在一条路径的,也就是要证明在G中存在s到v的一条路径。
而之所以DFS(s)能够在DFS(v)之前被调用,是因为在对G获取ReversePost-Order序列时,s出现在v之前,这也就意味着,v是在s之前加入该序列的(因为该序列使用栈作为数据结构,先加入的反而会在序列的后面)。因此根据DFS调用的递归性质,DFS(v)应该在DFS(s)之前返回,而有两种情形满足该条件:
- DFS(v) START -> DFS(v) END -> DFS(s) START -> DFS(s) END
- DFS(s) START -> DFS(v) START -> DFS(v) END -> DFS(s) END
是因为而根据目前的已知条件,GR中存在一条s到v的路径,即意味着G中存在一条v到s的路径,而在第一种情形下,调用DFS(v)却没能在它返回前递归调用DFS(s),这是和G中存在v到s的路径相矛盾的,因此不可取。故情形二为唯一符合逻辑的调用过程。而根据DFS(s) START -> DFS(v) START可以推导出从s到v存在一条路径。
所以从s到v以及v到s都有路径可达,证明完毕。
复杂度分析:
根据上面总结的Kosaraju算法关键步骤,不难得出,该算法需要对图进行两次DFS,以及一次图的转置。所以复杂度为O(V+E)。
