- 单片机物联网应用中的 Pogopin、串口与外围模组通信技术解析
麦德泽特
单片机物联网嵌入式硬件人工智能系统安全
引言在物联网蓬勃发展的当下,单片机作为关键的嵌入式设备核心,承担着数据采集、处理与控制的重任。而在单片机构建的物联网系统中,高效可靠的通信至关重要。Pogopin接口、串口通信以及各类外围模组的协同工作,为单片机与外部设备、网络之间搭建起了信息交互的桥梁。深入了解和掌握这些技术,对于优化物联网应用、提升系统性能具有重要意义。Pogopin接口:实现便捷连接1.1Pogopin原理与结构Pogopi
- 图像分割技术详解:从原理到实践
lanjieying
本文还有配套的精品资源,点击获取简介:图像分割是图像处理领域将图像分解为多个区域的过程,用于图像分析、特征提取等。文章介绍了图像分割的原理,并通过一个将图像划分为2*4子块的示例,展示了如何使用Python和matplotlib库中的tight_subplot函数进行图像分割和展示。文章还探讨了图像分割在不同领域的应用,以及如何在机器学习项目中作为数据预处理步骤。1.图像分割基本概念在图像处理领域
- ShaderGraph节点解析(136):矩形节点(Rectangle Node)详解
小李也疯狂
#UnityShaderGraphRectangle
目录一、节点功能概述二、端口详解三、控制选项四、技术原理解析4.1数学原理(距离场计算)4.2生成代码解析4.3视觉特性五、应用场景与实战案例5.1UI元素(矩形按钮/面板)场景:在UI中生成无纹理的矩形按钮或面板,支持动态调整大小和圆角(配合其他节点)5.2材质纹理(网格/条纹)场景:为材质添加矩形网格或条纹纹理(如布料格子、屏幕像素感)5.3粒子形状(矩形粒子/条纹)场景:控制粒子的形状为矩形
- ShaderGraph节点解析(124):绕轴旋转节点(Rotate About Axis Node)详解
小李也疯狂
#unityShaderGraphUnity
目录一、节点功能概述二、端口详解控制选项三、技术原理解析3.1数学基础:罗德里格斯旋转公式3.2旋转矩阵构造3.3生成代码解析1.弧度模式(Radians)2.度模式(Degrees)3.4旋转方向:右手定则四、应用场景与实战案例4.1角色骨骼旋转(动画驱动)场景:实现角色手臂绕肱骨(上臂骨)旋转,模拟弯曲动作4.2相机环绕效果(第三人称视角)场景:让相机绕目标物体(如角色)的Y轴旋转,实现环绕观
- Unity 内置着色器的使用与性能优化【Usage and Performance of Built-in Shaders】
小李也疯狂
#Shader:Built-inshadersunity着色器性能优化shader
Unity中的着色器通过材质(Material)应用,材质将着色器代码与纹理、颜色等参数结合。理解着色器与材质的关系及性能影响因素,对优化项目渲染效率至关重要。以下是内置着色器的使用指南与性能分析:一、着色器与材质的关系核心概念着色器(Shader):定义渲染逻辑(如光照计算、纹理混合),决定材质的属性和外观。材质(Material):着色器的实例,存储具体参数(如纹理、颜色值),同一着色器可创建
- 网络安全相关专业总结(非常详细)零基础入门到精通,收藏这一篇就够了
网络安全工程师教学
兼职副业黑客技术网络安全web安全安全人工智能网络运维
一、网络工程专业专业内涵网络工程是指按计划进行的以工程化的思想、方式、方法,设计、研发和解决网络系统问题的工程,一般指计算机网络系统的开发与构建。该专业培养具备计算机科学与技术学科理论基础,掌握网络技术领域专业知识和基本技能,在计算机、网络及人工智能领域的工程实践和应用方面受到良好训练,具有深厚通信背景、可持续发展、能力较强的高水平工程技术人才。学生可在计算机软硬件系统、互联网、移动互联网及新一代
- Esim:简化业务复杂度的Golang业务框架
周琰策Scott
Esim:简化业务复杂度的Golang业务框架esim微服务应用框架项目地址:https://gitcode.com/gh_mirrors/esi/esim项目介绍Esim是一款专注于解决业务复杂度、测试、代码组织和扩展等问题的Golang业务框架。它不提供微服务整套技术体系,如服务治理、服务注册、服务发现等,而是将这些交给了ServiceMesh。Esim默认集成了gin和grpc两个技术框架,
- 数据仓库技术及应用(Hive 产生背景与架构设计,存储模型与数据类型)
娟恋无暇
数据仓库笔记hive
1.Hive产生背景传统Hadoop架构存在的一些问题:MapReduce编程必须掌握Java,门槛较高传统数据库开发、DBA、运维人员学习门槛高HDFS上没有Schema的概念,仅仅是一个纯文本文件Hive的产生:为了让用户从一个现有数据基础架构转移到Hadoop上现有数据基础架构大多基于关系型数据库和SQL查询Facebook诞生了Hive2.Hive是什么官网:https://hive.ap
- STM32-架构分层与CMSIS实战指南
东方少爷
单片机单片机嵌入式硬件架构stm32硬件工程
从架构分层逻辑、CMSIS核心价值、内核与CMSIS协作关系三个维度,结合代码示例深度解析,并延伸到工程应用:一、STM32库架构分层解析(从硬件到应用)图中架构分为MCU层、CMSIS层、用户层,每层职责和文件分工明确:1.MCU层(硬件基础)包含内容:Cortex-M内核(如Cortex-M4)、SysTick、NVIC、调试模块、片上外设(GPIO、USART等)。作用:提供物理硬件能力,是
- 在Windows上构建本地服务器实现Augment团队邀请额度自动化增长的技术探索
yangshuo1281
windows服务器自动化
自动化:摘要:随着AI编码助手在开发领域日益普及,如何最大化利用这些工具的免费额度成为了许多开发者关心的话题。本文将以Augment为例,深入探讨一个技术爱好者的“极限挑战”:在Windows操作系统上,从零开始搭建一个本地全栈Web应用,以自动化方式完成团队邀请流程,从而实现免费使用额度的增长。本文不仅是一份操作指南,更是一次关于API交互、Web自动化、前后端开发的深度技术实践。在文章的最后,
- 【Python】python_jwt
宅男很神经
python开发语言
1.1传统会话(Session)机制的黄金时代与黄昏在Web应用的黎明时期,身份验证的范式几乎完全由**基于服务器端会话(Session-BasedAuthentication)**的机制所主导。这是一个直观且在单体应用时代极其有效的模型,其工作流程如同一场精密的双人舞:凭证交换与“储物柜钥匙”的签发:用户在登录页面输入用户名和密码。这些凭证被发送到服务器。服务器验证其有效性后,会在自己的“储物间
- 解锁数据结构“黑科技”:查表法的奇幻冒险
大雨淅淅
#数据结构数据结构算法开发语言
目录一、数据结构的“神秘地图”:认识查表法二、揭开查表法的神秘面纱(一)构建查找表(二)在表中进行查找三、实际案例大揭秘(一)案例一:简单数值查找(二)案例二:复杂关系查找四、查表法的优势与局限(一)优势尽显(二)局限剖析五、与其他查找方法的巅峰对决(一)与顺序查找的较量(二)与折半查找的比拼六、查表法的应用领域大赏(一)嵌入式系统中的“得力助手”(二)数据处理中的“高效利器”七、总结与展望一、数
- C#与SQL Server交互的数据库技术实践
不教书的塞涅卡
本文还有配套的精品资源,点击获取简介:本课程深入探讨C#与SQLServer数据库的交互技术,包括建立连接、执行SQL语句以及进行CRUD操作。详细介绍使用C#进行数据库操作时的核心概念与高级功能,如参数化查询、存储过程、事务处理、索引、视图和触发器等。旨在教授开发者如何高效、安全地管理和开发SQLServer数据库应用。1.C#与SQLServer的连接建立在现代软件开发中,后端服务经常需要与数
- 数据库的后悔药:Undo Log揭秘
你一身傲骨怎能输
游戏行业领域知识专栏撤销日志(UndoLog)
文章摘要撤销日志(UndoLog)是数据库的“后悔药”机制,用于保证数据操作的原子性和一致性。其核心原理是修改数据前先记录原始状态到UndoLog,若事务失败则进行回滚恢复。典型应用包括:1)事务回滚(如转账异常时还原数据);2)并发控制(通过快照读提供多版本视图)。主流数据库如MySQLInnoDB和Oracle均采用该技术,其流程可概括为“先备份后修改,出错即还原”。简言之,UndoLog通过
- 高效沟通05-FFC赞美法则
古城码农
工作记实录高效沟通沟通技巧
效沟通专栏–组织运转的命脉与个人成功的基石目录1.概念1.1底层逻辑1.2优势1.3适用场景1.4技巧2.示例1.概念 FFC是由三个英文单词首字母组成的结构化赞美模型,旨在让赞美真实可信、打动人心,避免空洞敷衍。其核心是通过三个层次构建逻辑闭环:要素含义作用关键要点F(Feeling)感受表达主观情感反应用情绪词传递真诚(如“感动”“佩服”)例:“你的方案让我非常惊喜!”F(Fact)事实提供
- Python知识点:如何使用memory_profiler进行内存分析
开篇,先说一个好消息,截止到2025年1月1日前,翻到文末找到我,赠送定制版的开题报告和任务书,先到先得!过期不候!如何使用memory_profiler进行Python代码内存分析在开发高性能的Python应用程序时,理解和优化内存使用是至关重要的。memory_profiler是一个强大的工具,它可以帮助你监控Python代码的内存使用情况。本文将介绍如何使用memory_profiler来分
- 大语言模型应用指南:ReAct 框架
AI大模型应用实战
javapythonjavascriptkotlingolang架构人工智能
大语言模型应用指南:ReAct框架关键词:大语言模型,ReAct框架,自然语言处理(NLP),模型融合,多模态学习,深度学习,深度学习框架1.背景介绍1.1问题由来近年来,深度学习技术在自然语言处理(NLP)领域取得了显著进展。尤其是大语言模型(LargeLanguageModels,LLMs),如BERT、GPT系列等,通过在大规模无标签数据上进行预训练,获得了强大的语言理解和生成能力。然而,预
- 2019年架构师系列教程:高并发Netty实战打造百万连接架构
不教书的塞涅卡
本文还有配套的精品资源,点击获取简介:本课程面向高级IT专业人士,旨在教授如何利用Netty框架设计和实现能够处理高并发连接的服务器架构。Netty是一个高性能、异步事件驱动的Java网络应用程序框架。课程将提升学员在系统架构设计和性能优化方面的技能,应对高并发场景挑战,特别是在金融、游戏、物联网等领域。1.Netty框架基础概念介绍Netty是一个高性能的网络应用框架,专为快速开发可维护的高性能
- Android之Application的onTerminate能监听应用退出吗?
zhangphil
AndroidAndroid
Android之Application的onTerminate能监听应用退出吗?一些Android开发者在不经意间发现Android的Application中有一个公开的回调方法:onTerminate()继而想当然的认为该方法即是Android的整个App应用退出后的回调,因为Terminate的词面意思就是结束,终结嘛。那么onTerminate在Android的App全部结束后回调,真的是这
- Pillow 安装使用教程
小奇JAVA面试
安装使用教程pillowmicrosoft深度学习
一、Pillow简介Pillow是Python图像处理库PIL(PythonImagingLibrary)的友好分支,是图像处理的事实标准。它支持打开、编辑、转换、保存多种图像格式,常用于图像批量处理、验证码识别、缩略图生成等应用场景。二、安装Pillow2.1使用pip安装(推荐)pipinstallPillow2.2验证安装importPILprint(PIL.__version__)若无报错
- 9、并行计算在现代计算中的应用与优化
seed
探索并行计算与HPC新范式并行计算高性能计算大数据分析
并行计算在现代计算中的应用与优化1.引言并行计算作为一种高效的计算模式,近年来在工业和学术界得到了广泛的应用和发展。随着计算需求的不断增加,传统的串行计算模式已经难以满足现代复杂问题的需求。并行计算通过将计算任务分解为多个子任务,并在多个处理单元上同时执行,从而显著提高了计算效率。本文将探讨并行计算在现代计算中的应用与优化,重点介绍并行计算的基本原理、应用场景和技术细节。2.并行计算的基本原理并行
- Java面试八股文(2023最新)--Linux面试题
月月崽
面试linux运维服务器
目录1.什么是Linux内核2.Linux的体系结构.4.基本命令5.如何查看最近1000行日志6.如何查端口号是否被占用7.查看当前所有已经使用的端口情况8.什么是硬链接和软链接?1.什么是Linux内核Linux系统的核心是内核,内核控制着计算机系统上的软硬件,在必要时分配硬件,并根据需要执行软件.系统内存管理应用程序管理硬件设备管理文件系统管理2.Linux的体系结构.Linux体系结构可以
- Java面试八股文(2023最新)--Redis面试题
月月崽
面试javaredis面试
目录1.什么是Redis?2.Redis的优缺点?3.Redis有哪些数据结构?4.Redis的应用场景5.持久化?6.Redis的持久化机制是什么?有什么优缺点?7.Redis的过期删除策略?8.Redis的内存淘汰策略有哪些?9.Redis的事务保证原子性吗,支持回滚吗?10.什么是Redis穿透?10.什么是Redis击穿?11.什么是redis雪崩?12.使用Redis作为缓存,Redis
- torch.nn.init.kaiming_normal_
参考(5条消息)PytorchKaiming初始化(Initialization)中fan_in和fan_out的区别/应用场景_bxdzyhx的博客-CSDN博客torch.nn.init.kaiming_normal_使用正态分布对输入张量进行赋值fan_in如果权重是通过线性层(卷积或全连接)隐性确定的,则需设置mode=fan_in。例子:importtorchlinear_layer=t
- DeepSeek AI全面应用:AI时代的高效办公与创意生产指南
Want595
人工智能deepseek
京东链接:https://item.jd.com/15045868.html当当链接:https://product.dangdang.com/29893005.html文章目录写在前面核心亮点1.直击痛点:从“低效搬砖”到“智能掌控”2.创意觉醒:让AI成为你的“灵感引擎”3.跨平台协作:无缝衔接AI生态4.实战驱动:130+案例,即学即用5.超值资源包:扫码即得适合谁读1.职场人2.创作者/自
- 目前最火的agent方向-A2A快速实战构建(二): AutoGen模型集成指南:从OpenAI到本地部署的全场景LLM解决方案
引言:打破模型壁垒,构建灵活AI应用在AI应用开发中,大语言模型(LLM)的选择往往决定了系统的能力边界。AutoGen通过标准化的模型客户端协议,实现了对OpenAI、AzureOpenAI、本地模型等多源LLM的统一接入,让开发者能够根据场景需求自由切换模型服务。本文将深入解析AutoGen的模型集成框架,从云端服务到本地部署,助你构建弹性可扩展的AI代理系统。一、模型客户端核心架构:统一接口
- 深入解析Spring Boot与Kafka集成:构建高效消息驱动应用
深入解析SpringBoot与Kafka集成:构建高效消息驱动应用引言在现代分布式系统中,消息队列技术扮演着至关重要的角色。ApacheKafka作为一款高性能、分布式的消息队列系统,被广泛应用于实时数据处理、日志收集、事件驱动架构等场景。本文将深入探讨如何在SpringBoot应用中集成Kafka,构建高效的消息驱动应用。1.Kafka简介ApacheKafka是一个分布式流处理平台,具有高吞吐
- 深入解析Spring Boot与Kafka集成:构建高效消息驱动微服务
Uranus^
JavaSpringBootKafka微服务消息队列
深入解析SpringBoot与Kafka集成:构建高效消息驱动微服务引言在现代微服务架构中,消息队列扮演着至关重要的角色,尤其是在处理高并发、异步通信和解耦系统组件时。ApacheKafka作为一款高性能的分布式消息队列系统,被广泛应用于实时数据处理和事件驱动架构中。本文将深入探讨如何在SpringBoot应用中集成Kafka,构建高效的消息驱动微服务。1.Kafka简介ApacheKafka是一
- 深入解析Spring Boot与Kafka集成:构建高性能消息驱动应用
Uranus^
JavaSpringBootKafka消息队列分布式系统
深入解析SpringBoot与Kafka集成:构建高性能消息驱动应用引言在现代分布式系统中,消息队列是实现异步通信和解耦的关键组件之一。ApacheKafka作为一种高性能、分布式的消息队列系统,被广泛应用于大数据处理、实时流处理以及事件驱动的架构中。本文将深入探讨如何在SpringBoot应用中集成Kafka,构建高性能的消息驱动应用。Kafka简介ApacheKafka是一个分布式流处理平台,
- 【XML笔记】XML入门_XML文档的创建
追云的帆
JavaWebxml文档
一.XML1.概述:XML是ExtensibleMarkupLanguage可扩展标记语言是SGML(标准通用化标记语言)的一个子集,用于提供数据描述格式,适用于不同应用程序间的数据交换,这种交换不以预先定义的数据结构为前提,增强了可扩展性。一个基本的XML文档由序言和文档元素两部分构成2.序言在XML文档的第一行通常是XML声明,用于说明这是一个XML文档。XML声明的语法格式如下:versio
- apache ftpserver-CentOS config
gengzg
apache
<server xmlns="http://mina.apache.org/ftpserver/spring/v1"
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="
http://mina.apache.o
- 优化MySQL数据库性能的八种方法
AILIKES
sqlmysql
1、选取最适用的字段属性 MySQL可以很好的支持大数据量的存取,但是一般说来,数据库中的表越小,在它上面执行的查询也就会越快。因此,在创建表的时候,为了获得更好的 性能,我们可以将表中字段的宽度设得尽可能小。例如,在定义邮政编码这个字段时,如果将其设置为CHAR(255),显然给数据库增加了不必要的空间,甚至使用VARCHAR这种类型也是多余的,因为CHAR(6)就可以很
- JeeSite 企业信息化快速开发平台
Kai_Ge
JeeSite
JeeSite 企业信息化快速开发平台
平台简介
JeeSite是基于多个优秀的开源项目,高度整合封装而成的高效,高性能,强安全性的开源Java EE快速开发平台。
JeeSite本身是以Spring Framework为核心容器,Spring MVC为模型视图控制器,MyBatis为数据访问层, Apache Shiro为权限授权层,Ehcahe对常用数据进行缓存,Activit为工作流
- 通过Spring Mail Api发送邮件
120153216
邮件main
原文地址:http://www.open-open.com/lib/view/open1346857871615.html
使用Java Mail API来发送邮件也很容易实现,但是最近公司一个同事封装的邮件API实在让我无法接受,于是便打算改用Spring Mail API来发送邮件,顺便记录下这篇文章。 【Spring Mail API】
Spring Mail API都在org.spri
- Pysvn 程序员使用指南
2002wmj
SVN
源文件:http://ju.outofmemory.cn/entry/35762
这是一篇关于pysvn模块的指南.
完整和详细的API请参考 http://pysvn.tigris.org/docs/pysvn_prog_ref.html.
pysvn是操作Subversion版本控制的Python接口模块. 这个API接口可以管理一个工作副本, 查询档案库, 和同步两个.
该
- 在SQLSERVER中查找被阻塞和正在被阻塞的SQL
357029540
SQL Server
SELECT R.session_id AS BlockedSessionID ,
S.session_id AS BlockingSessionID ,
Q1.text AS Block
- Intent 常用的用法备忘
7454103
.netandroidGoogleBlogF#
Intent
应该算是Android中特有的东西。你可以在Intent中指定程序 要执行的动作(比如:view,edit,dial),以及程序执行到该动作时所需要的资料 。都指定好后,只要调用startActivity(),Android系统 会自动寻找最符合你指定要求的应用 程序,并执行该程序。
下面列出几种Intent 的用法
显示网页:
- Spring定时器时间配置
adminjun
spring时间配置定时器
红圈中的值由6个数字组成,中间用空格分隔。第一个数字表示定时任务执行时间的秒,第二个数字表示分钟,第三个数字表示小时,后面三个数字表示日,月,年,< xmlnamespace prefix ="o" ns ="urn:schemas-microsoft-com:office:office" />
测试的时候,由于是每天定时执行,所以后面三个数
- POJ 2421 Constructing Roads 最小生成树
aijuans
最小生成树
来源:http://poj.org/problem?id=2421
题意:还是给你n个点,然后求最小生成树。特殊之处在于有一些点之间已经连上了边。
思路:对于已经有边的点,特殊标记一下,加边的时候把这些边的权值赋值为0即可。这样就可以既保证这些边一定存在,又保证了所求的结果正确。
代码:
#include <iostream>
#include <cstdio>
- 重构笔记——提取方法(Extract Method)
ayaoxinchao
java重构提炼函数局部变量提取方法
提取方法(Extract Method)是最常用的重构手法之一。当看到一个方法过长或者方法很难让人理解其意图的时候,这时候就可以用提取方法这种重构手法。
下面是我学习这个重构手法的笔记:
提取方法看起来好像仅仅是将被提取方法中的一段代码,放到目标方法中。其实,当方法足够复杂的时候,提取方法也会变得复杂。当然,如果提取方法这种重构手法无法进行时,就可能需要选择其他
- 为UILabel添加点击事件
bewithme
UILabel
默认情况下UILabel是不支持点击事件的,网上查了查居然没有一个是完整的答案,现在我提供一个完整的代码。
UILabel *l = [[UILabel alloc] initWithFrame:CGRectMake(60, 0, listV.frame.size.width - 60, listV.frame.size.height)]
- NoSQL数据库之Redis数据库管理(PHP-REDIS实例)
bijian1013
redis数据库NoSQL
一.redis.php
<?php
//实例化
$redis = new Redis();
//连接服务器
$redis->connect("localhost");
//授权
$redis->auth("lamplijie");
//相关操
- SecureCRT使用备注
bingyingao
secureCRT每页行数
SecureCRT日志和卷屏行数设置
一、使用securecrt时,设置自动日志记录功能。
1、在C:\Program Files\SecureCRT\下新建一个文件夹(也就是你的CRT可执行文件的路径),命名为Logs;
2、点击Options -> Global Options -> Default Session -> Edite Default Sett
- 【Scala九】Scala核心三:泛型
bit1129
scala
泛型类
package spark.examples.scala.generics
class GenericClass[K, V](val k: K, val v: V) {
def print() {
println(k + "," + v)
}
}
object GenericClass {
def main(args: Arr
- 素数与音乐
bookjovi
素数数学haskell
由于一直在看haskell,不可避免的接触到了很多数学知识,其中数论最多,如素数,斐波那契数列等,很多在学生时代无法理解的数学现在似乎也能领悟到那么一点。
闲暇之余,从图书馆找了<<The music of primes>>和<<世界数学通史>>读了几遍。其中素数的音乐这本书与软件界熟知的&l
- Java-Collections Framework学习与总结-IdentityHashMap
BrokenDreams
Collections
这篇总结一下java.util.IdentityHashMap。从类名上可以猜到,这个类本质应该还是一个散列表,只是前面有Identity修饰,是一种特殊的HashMap。
简单的说,IdentityHashMap和HashM
- 读《研磨设计模式》-代码笔记-享元模式-Flyweight
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.Collection;
import java.util.HashMap;
import java.util.List;
import java
- PS人像润饰&调色教程集锦
cherishLC
PS
1、仿制图章沿轮廓润饰——柔化图像,凸显轮廓
http://www.howzhi.com/course/retouching/
新建一个透明图层,使用仿制图章不断Alt+鼠标左键选点,设置透明度为21%,大小为修饰区域的1/3左右(比如胳膊宽度的1/3),再沿纹理方向(比如胳膊方向)进行修饰。
所有修饰完成后,对该润饰图层添加噪声,噪声大小应该和
- 更新多个字段的UPDATE语句
crabdave
update
更新多个字段的UPDATE语句
update tableA a
set (a.v1, a.v2, a.v3, a.v4) = --使用括号确定更新的字段范围
- hive实例讲解实现in和not in子句
daizj
hivenot inin
本文转自:http://www.cnblogs.com/ggjucheng/archive/2013/01/03/2842855.html
当前hive不支持 in或not in 中包含查询子句的语法,所以只能通过left join实现。
假设有一个登陆表login(当天登陆记录,只有一个uid),和一个用户注册表regusers(当天注册用户,字段只有一个uid),这两个表都包含
- 一道24点的10+种非人类解法(2,3,10,10)
dsjt
算法
这是人类算24点的方法?!!!
事件缘由:今天晚上突然看到一条24点状态,当时惊为天人,这NM叫人啊?以下是那条状态
朱明西 : 24点,算2 3 10 10,我LX炮狗等面对四张牌痛不欲生,结果跑跑同学扫了一眼说,算出来了,2的10次方减10的3次方。。我草这是人类的算24点啊。。
然后么。。。我就在深夜很得瑟的问室友求室友算
刚出完题,文哥的暴走之旅开始了
5秒后
- 关于YII的菜单插件 CMenu和面包末breadcrumbs路径管理插件的一些使用问题
dcj3sjt126com
yiiframework
在使用 YIi的路径管理工具时,发现了一个问题。 <?php
- 对象与关系之间的矛盾:“阻抗失配”效应[转]
come_for_dream
对象
概述
“阻抗失配”这一词组通常用来描述面向对象应用向传统的关系数据库(RDBMS)存放数据时所遇到的数据表述不一致问题。C++程序员已经被这个问题困扰了好多年,而现在的Java程序员和其它面向对象开发人员也对这个问题深感头痛。
“阻抗失配”产生的原因是因为对象模型与关系模型之间缺乏固有的亲合力。“阻抗失配”所带来的问题包括:类的层次关系必须绑定为关系模式(将对象
- 学习编程那点事
gcq511120594
编程互联网
一年前的夏天,我还在纠结要不要改行,要不要去学php?能学到真本事吗?改行能成功吗?太多的问题,我终于不顾一切,下定决心,辞去了工作,来到传说中的帝都。老师给的乘车方式还算有效,很顺利的就到了学校,赶巧了,正好学校搬到了新校区。先安顿了下来,过了个轻松的周末,第一次到帝都,逛逛吧!
接下来的周一,是我噩梦的开始,学习内容对我这个零基础的人来说,除了勉强完成老师布置的作业外,我已经没有时间和精力去
- Reverse Linked List II
hcx2013
list
Reverse a linked list from position m to n. Do it in-place and in one-pass.
For example:Given 1->2->3->4->5->NULL, m = 2 and n = 4,
return
- Spring4.1新特性——页面自动化测试框架Spring MVC Test HtmlUnit简介
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- Hadoop集群工具distcp
liyonghui160com
1. 环境描述
两个集群:rock 和 stone
rock无kerberos权限认证,stone有要求认证。
1. 从rock复制到stone,采用hdfs
Hadoop distcp -i hdfs://rock-nn:8020/user/cxz/input hdfs://stone-nn:8020/user/cxz/运行在rock端,即源端问题:报版本
- 一个备份MySQL数据库的简单Shell脚本
pda158
mysql脚本
主脚本(用于备份mysql数据库): 该Shell脚本可以自动备份
数据库。只要复制粘贴本脚本到文本编辑器中,输入数据库用户名、密码以及数据库名即可。我备份数据库使用的是mysqlump 命令。后面会对每行脚本命令进行说明。
1. 分别建立目录“backup”和“oldbackup” #mkdir /backup #mkdir /oldbackup
- 300个涵盖IT各方面的免费资源(中)——设计与编码篇
shoothao
IT资源图标库图片库色彩板字体
A. 免费的设计资源
Freebbble:来自于Dribbble的免费的高质量作品。
Dribbble:Dribbble上“免费”的搜索结果——这是巨大的宝藏。
Graphic Burger:每个像素点都做得很细的绝佳的设计资源。
Pixel Buddha:免费和优质资源的专业社区。
Premium Pixels:为那些有创意的人提供免费的素材。
- thrift总结 - 跨语言服务开发
uule
thrift
官网
官网JAVA例子
thrift入门介绍
IBM-Apache Thrift - 可伸缩的跨语言服务开发框架
Thrift入门及Java实例演示
thrift的使用介绍
RPC
POM:
<dependency>
<groupId>org.apache.thrift</groupId>
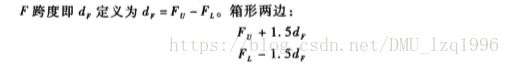



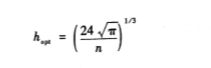 除了h影响直方图形状外,起始点x0也影响直方图形状。——移动平均直方图
除了h影响直方图形状外,起始点x0也影响直方图形状。——移动平均直方图