从洛伦兹曲线定性地看马太效应的根源

以往之不鉴，来者之可追！ —2018/03/04中午做了家乡的扁粉菜后手记

穷的本质是什么？富又意味着什么？你知道为什么我们的贫富差距那么大吗？你知道为什么你那么穷或者那么富吗？是少数富人太恶毒？还是大量穷人太不努力？…

---

当我们在讨论社会财富分配或者社交网络等话题的时候，往往避不开的概念包括马太效应，幂律等。大致上的意思是在说，不到20%的人占有了超过80%的财富，只有不到20%的网络节点却拥有了整个网络超过80%的链接数。在以往，我以可以将这种现象通俗地理解成80/20原则或者二八定律，然而这种描述毕竟不是很精确，我们期待用数学来描述这种现象，于是很早以前就诞生了很多相关的数学理论，比如幂律等。

  幂律的数学表述和相关证明请看我年前写的文章，这里不再赘述：
马太效应/幂律分布的本质以及其数学表述：http://blog.csdn.net/dog250/article/details/79146511

---

然而，非常令人遗憾的是，现实中的世界是及其复杂的，每一个方面的每一个细节因素都会被所有其它方面的其它细节因素所影响，这在数学上是一个不可解的问题，因此，幂律的数学描述终究是对社会现实理想化的描述，这正如力学中光滑平面一样…

---

更多的时候，我们要想分析一种社会化的现象，能拿到的只是一些散点数据，我们要通过这些散点数据得到一些具有统计意义的结论，比如：

• 社会财富到底真的是幂律分布，还是正态分布的呢？
• 现如今的学区房分配方法对大多数人公平吗？
• …

洛伦兹曲线

感谢洛伦兹曲线，使得我们可以在一幅图中归纳总结并看清楚这一切。那么，什么是洛伦兹曲线？我通过社会财富分配的例子用自己的语言先简单描述一下。

• 第一，画出横坐标。让参与财富分配的人按照自己收入从低到高依次从左到右等距排队；
  
• 第二，画出纵坐标。横坐标任意区间对应的那部分人在纵坐标对应区间表示他们的财富所占总财富的比例。

• 第三，描点。把所有的散点描入基于上面两步建立的坐标系中，用平滑曲线将它们相连，这就是洛伦兹曲线。

我这里的介绍很简单，更详细的描述请自行搜索相关文献。接下来我主要说一下洛伦兹曲线的一些性质以及我们如何从这条曲线上看出一些更为细节的东西。我的目标是希望能在一幅图上看到更多的东西。

---

洛伦兹曲线的性质

由于洛伦兹曲线的横坐标表示的人口是按照收入从低到高排队的，那么曲线从左到右，每增加一个人，其对积累人口财富比例的贡献应该是逐步增加。换句话说，曲线的斜率正是该点所对应人口的收入绝对值(归一化后的绝对值)，由于横坐标是排序的，所以我们得出一个性质：

洛伦兹曲线一定是下凸的，随着横坐标增加，其对应点的斜率单调递增。

  另外，横坐标上的点到原点的距离表示的是积累人口，把所有人口作为单位1并取百分比的话，横坐标的做大标度就是1，而纵坐标表示财富百分比，它的最大标度自然就是1，也就是100%，因此，有第二个性质：

洛伦兹曲线被围在 (0,0) ( 0 , 0 ) ， (100%,0) ( 100 % , 0 ) ， (100%,100%) ( 100 % , 100 % ) ， (0,100%) ( 0 , 100 % ) 这个四方块中。

另外，还有一个性质，即：

曲线的斜率表示该点人口的收入值

有了上面3个性质，我们就可以进行分析曲线的形状了，看看都能得到什么结论，这是比较有意思的事，我之前也是基于这个兴趣分析Wireshark的tcptrace曲线的…

---

所有人收入都一样的情况

很显然，所有人收入都一样的时候，洛伦兹曲线是一条直线，毕竟只有直线的斜率是不会变化的。

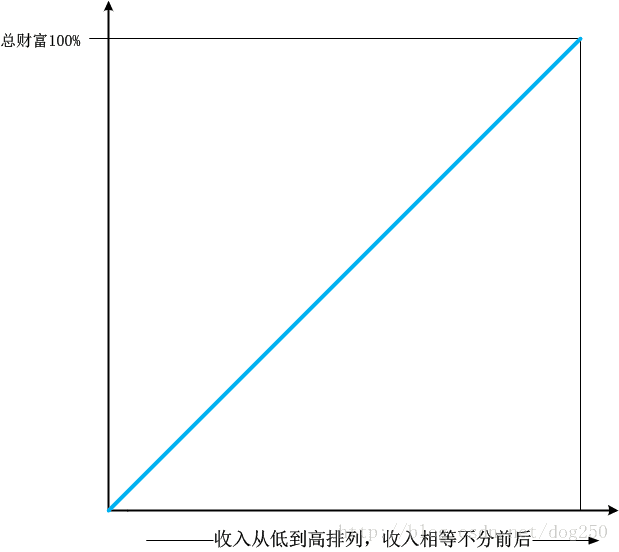
该直线的方程是：
y=x y = x

正态分布的情况

正态分布的意思是，巨穷和巨富都很少，大部分人收入都差不多，先简单点说吧，假设有1000人，其中2人巨穷，收入只有10元，2人巨富，收入有100元，其余所有人收入都是50元，这就是一个正态分布：

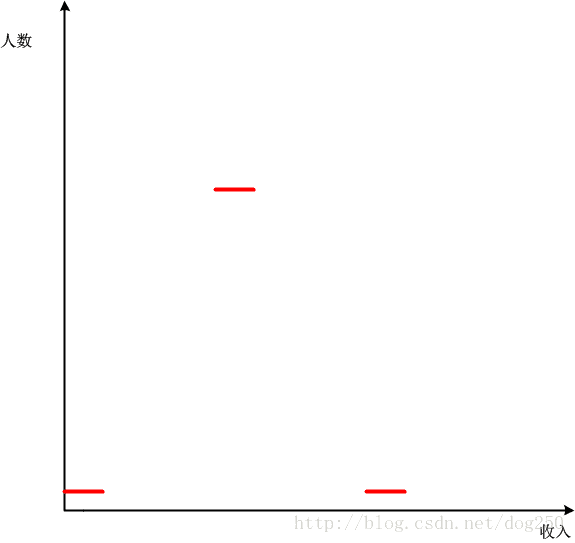
我们把它的洛伦兹曲线大致画出来。注意，由于本例中只有3种收入，不存在渐变，所以洛伦兹曲线应该由3段线端构成：

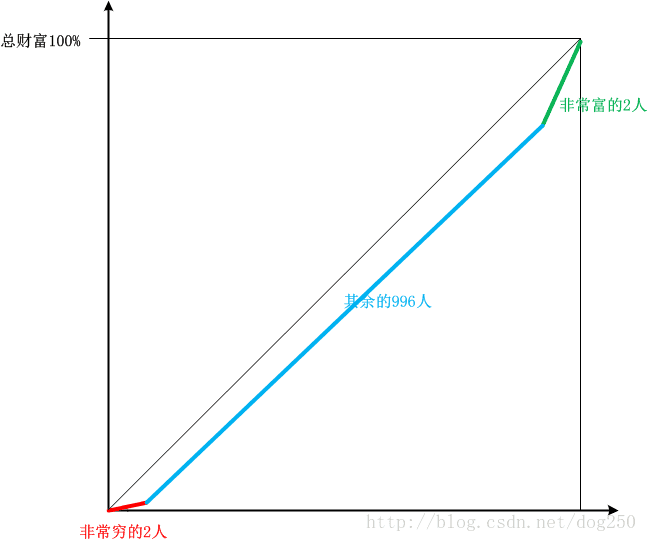
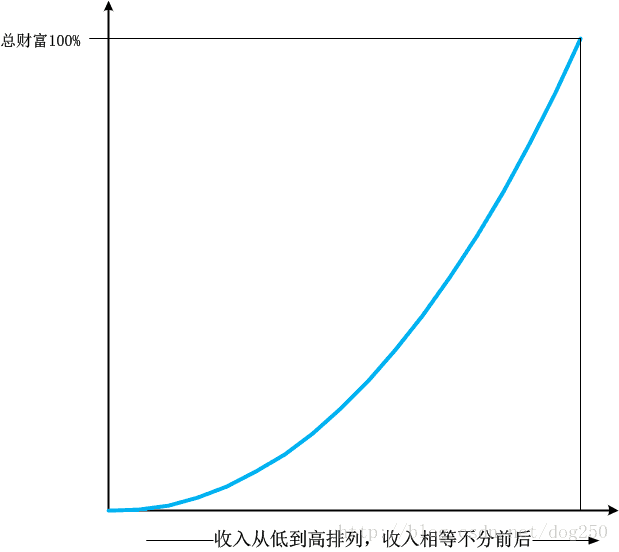
实际的正态分布并不是这样，它看起来是下面的样子：

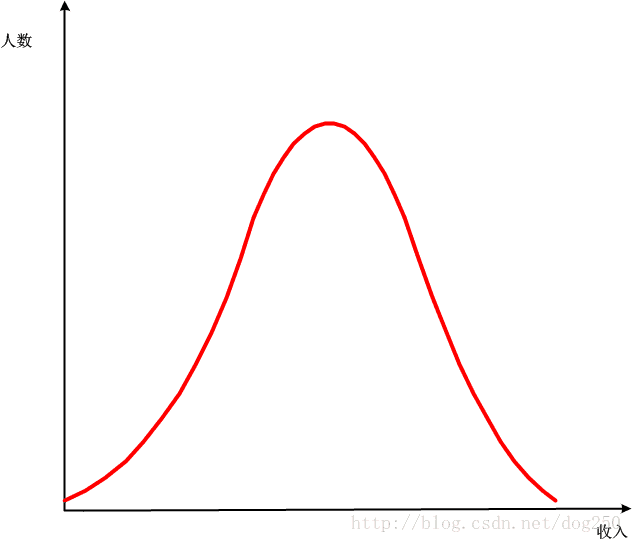
它是自相似的，也就是从下到上随意截取局部，其结果均是一个新的正态分布：

因此，洛伦兹曲线也可以用相似的方式画出：

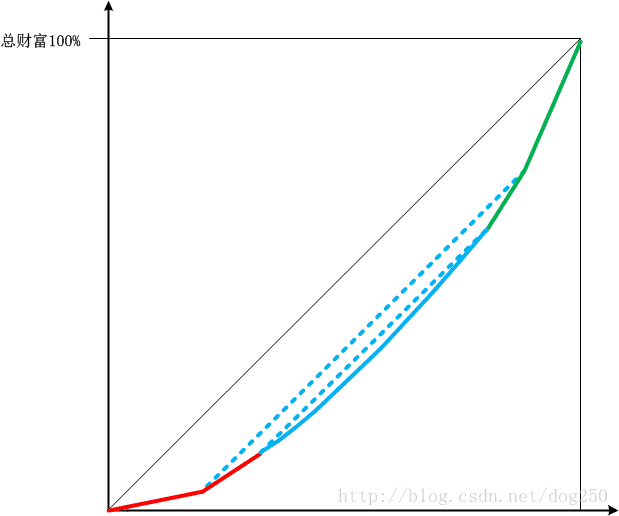
其实就是不断的放大局部并细化，类似分形那般。

马太效应或者幂律的情况

现在该看幂律了。这也是我们的重点。

  显然，你不能说社会财富的分配就一定是幂律，这太抽象了，并且它没有精确的数据支撑，比方说我给出一个幂函数的公式，画出曲线，你能保证每一个人的收入都在曲线上有对应点吗？显然不能。

  你只能笼统的说，社会上小部分人占有了巨量的财富，这小部分小到什么程度，这财富巨量到什么程度，并无法用一个公式来给出，社会不是数学的，社会是统计的。很失望，不是吗？不过，还是有希望的，我们可以通过统计采集得到的实际散点数据，按照本文的方法描出洛伦兹曲线，来看看到底是不是一小撮人占据了巨量的财富。

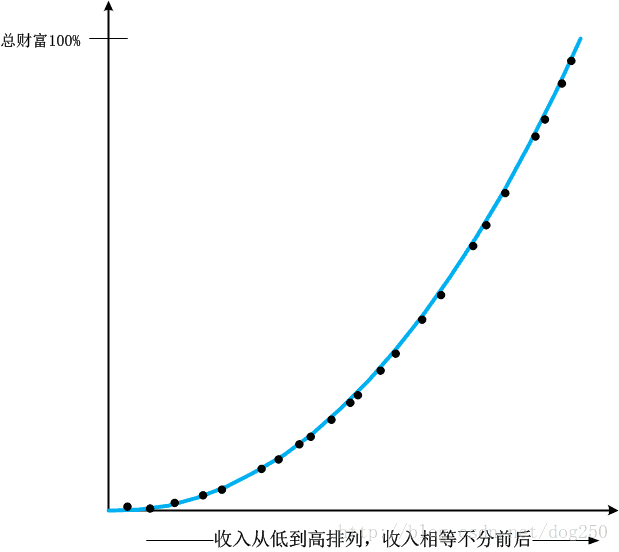
  实际的数据分析这里就不说了，可以从国家或者各省的统计年鉴中获取，并且用工具将其导出并分析。本文给出一个虽然假但是却很典型的图，让我们直接来看一下：

这是不是幂律我不知道，但这确实是马太效应的意思了吧。洛伦兹曲线的妙处在于，它能很好地定性表示资源分配的平等性特征。

  数学是抽象出来的，也许财富分配情况或者网络节点链接情况的实际数据并不在任何一个幂次方程的曲线上，但是定性地来讲，它可能表达的确实就是《新约.马太福音》里的意思，这显然是一个普遍现象，至少在古罗马帝国初创时期就已经表现了出来！

  但是，且慢！马太效应说的是少量富人的情况，显然不公平就是那些个少量富人引起的，但是反过来，不公平能不能是少量穷人引起的呢？或者不公平会不会是大量穷人引起的呢？且看下节！

少量穷人或者大量穷人

在数学上，我们认为对称是一种美，甚至在哲学上，有人认为时间会反演，甚至贝叶斯公式也体现了这个道理，那就更别提什么量子力学里面那些玄之又玄的道理了…

  我们知道，穷和富是一对反义词，既然少量的巨富能引起不公平甚至类似1789年法国发生的事情，那么少量的穷人会不会有同样的效果呢？我们画出洛伦兹曲线便可以知晓究竟：

可见，如果只有少量的穷人，不会引起不公平，在社会财富总量一定的情况下，在洛伦兹曲线被完全公平线围住的情况下，意味着中产阶级的收入不会高出平均收入太多。

  上面这个图如果你离远了眯着眼睛看，会发现该洛伦兹曲线和完全公平线并没有分开太多，再远一点，它们几乎是重合的…阿尔伯特·赫希曼正是基于此提出了所谓“基尼指数”的概念，用来衡量资源分配的公平性，但这是后话…

  那么，如果有巨量的穷人呢？我们再来看这时候的洛伦兹曲线：

情况完全不同了…为什么在数学上以及在描述上完全对称的穷和富，在洛伦兹曲线上会发生如此大的差异？因为财富是非负的，它在熵的意义上并不对称：你的财富被平均导致了你穷，这是一件不需要努力的事，这是熵的自然增加，反过来，如果你想富就必须主动降低熵值，那么自己就是一个低熵体了！

  所以这里有个社会学的结论，如果你觉得不公平，十有八九是因为你自己，没有人可以空手套白狼，另外十分之一二就是1789年法国的人们走向街头的理由！

---

基尼指数

上面的小节基本上已经很明确的描述了洛伦兹曲线的读法，但是现在，我们还缺少一个定量的东西没有介绍，它就是基尼指数，或者叫基尼系数，这个值就是资源分配不公平程度的度量

  按照常理，一般人都会觉得洛伦兹曲线在先，基尼指数在后，一个叫做XXX的人在像我这样观察了洛伦兹曲线后，会发现一种衡量资源分配公平性的一种计算方法。

  不卖关子，其实我们可以用洛伦兹曲线偏离公平线的程度来衡量上述指标，定量来讲，那就是求出下列面积的比值即可：
AA+B A A + B

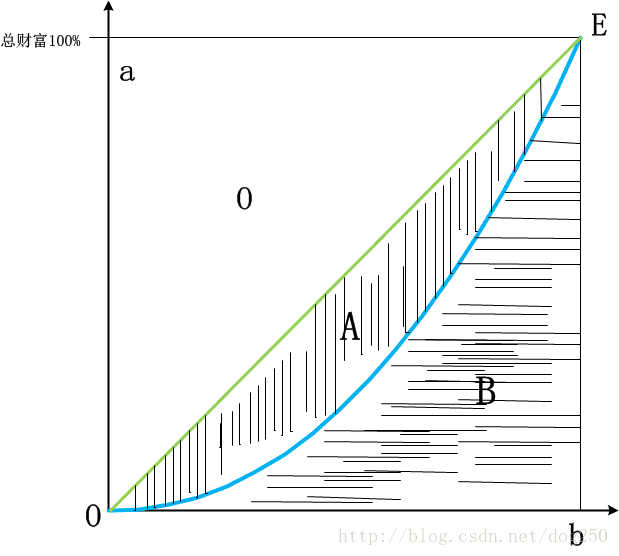
如果我们又洛伦兹曲线的方程式，那么就可以很容易用定积分来求出各部分面积，从而得到基尼指数的值了。

  现在的问题是如何得到洛伦兹曲线的方程！

  这很容易，有各种拟合方案！懂的人都知道，简单点说，就是用类似线性回归以及诸如二项式，泰勒展开的方法，为一条散点描述出的任意曲线寻找一条可以用数学式子表达的规则曲线，可以用二次曲线，三次曲线，四次曲线…去拟合，有了数学式子，便可以随心所欲了！

  当然，你我都知道，这个数学式子只是拟合的结果，并不是100%精确匹配，要知道，100%精确匹配的数学式子几乎不存在！

基尼指数的遗漏

可以看出，基尼指数只是计算出来的一个数值，它妥妥的是个标量而不是向量，你能从这个值里得到不同的解释。

  显然，这个值是计算面积的比值得到的，还是以穷人与富人举例，我们看看下面的两条洛伦兹曲线：

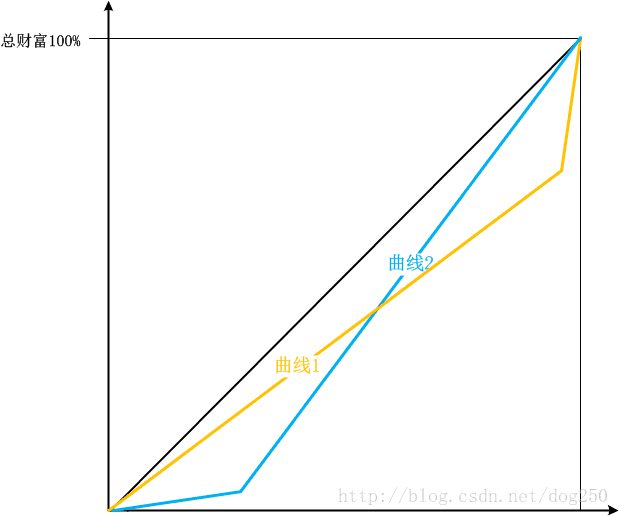
很显然两条曲线所计算出的基尼指数是相同的，但二者的问题的原因却是相反的。从曲线1可以看出，问题的根源在于富人，而从曲线2可以看出，问题则是由于少数穷人导致的，虽然基尼指数相同，但是从洛伦兹曲线走向的差异可以指导相关的策略是对富人收税还是对穷人补贴，这二者的结果显然差异巨大。

  无论如何，上面的例子虽然看起来两条曲线的基尼指数是相同的，但是两条曲线总体看来其基尼指数都不是太大，现在的问题是，如果基尼指数很大，我们必须将其归结成一种原因，而不能是两个相反的原因，从图上看，确实可能存在两种相反的原因导致相同的基尼指数，这并不是我们想要的。注意，我的理论要来了，单独列出一个小节

---

不公平只能由一个原因引起

由于完全公平线的存在，只要有穷人或者有富人，洛伦兹曲线就会往右往下被拉伸！往右拉伸增加了穷人的数量，往下拉伸增加了富人的财富！这确实是一个正反馈关系，这就是穷者越穷，富者越富的根源！这就是马太效应！后面的小节会继续阐述这个根源的解释，但是在本节，我会先给出一个收敛模型，旨在证明，无论是穷人多，还是富人多，最终它们均收敛到同一个点，即严重的问题发生，只有一个主要原因，而不会是两个或者多个。

  先看下图，我的模型都在图里，注意两条关于
y=−x+1 y = − x + 1
对称的洛伦兹曲线(显然其基尼指数是相同的)关键拐点(收入开始大于平均收入的点！)之间的距离：

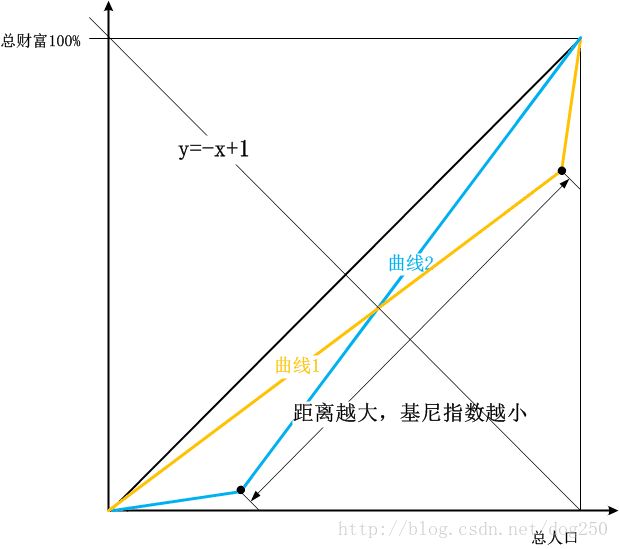
从图上可以看出，如果那两个黑点中的其中一个向着直线 y=−x+1 y = − x + 1 靠近，关于其对称的另一条也会向其靠近，最终二者的收敛点就是在直线 y=−x+1 y = − x + 1 上。

  接下来我们只需讨论关键拐点在 y=−x+1 y = − x + 1 上的情况就好了：

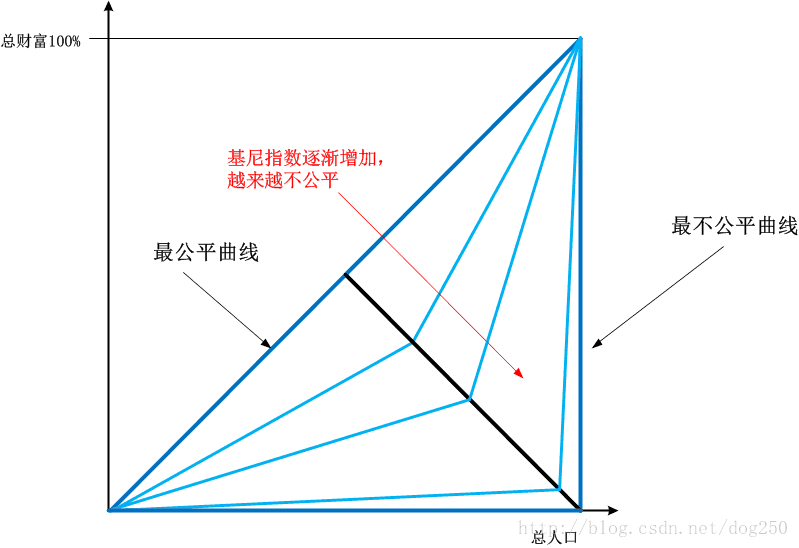
看来，用面积的比值计算而得到的基尼指数，真的可以直观地表示出不公平程度。现在的问题是，洛伦兹曲线能否提供一种动力学的解释，让我们看到更加深刻的造就这条曲线的内在原因呢？就是说“巨大的不公平(即马太效应)到底是大量的穷人导致的呢，还是少量富人导致的呢？”，这就是在问：

是大量的穷人造就了少量富人呢，还是少量富人引起了大量穷人的产生？

诡异的因果轮回

上节最后的提问，我相信大多数的回答是后者，或者情愿认为是后者，然而，我觉得恰恰相反，马太效应的根源在于大量穷人的不努力，而不是少量富人的努力，这个结论用于针对链接数计量权重的复杂网络也是适用的，比如社交圈，比如互联网。

  我就问下面两种平衡哪种更容易维持吧：

必然是第一个更容易维持平衡，因为不需要费劲，这是一个负反馈，而第二个平衡如果想维持，必然要持续注入能量，这是一个正反馈，一旦偏离，便万劫不复地跌落。这非常好理解，你想穷的话，简单放松任其自然就好了，如果想富，就必然不断努力，即便你想搞点不义之财，也不能守株待兔吧…

  假设一开始财富(包括任意资源)的分配是公平的，我们来看看事情如何演化：

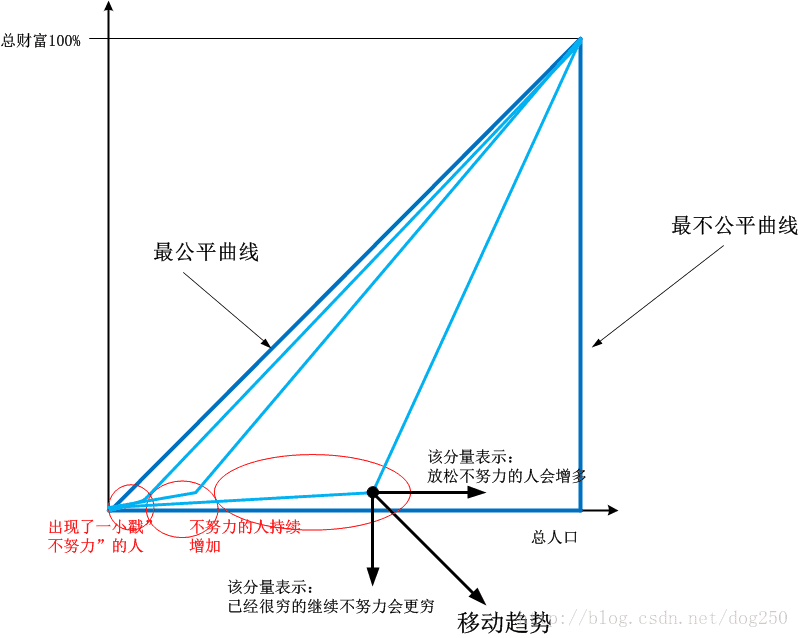
理解为什么一开始有人会在完全公平的时候首先变穷非常容易，你只需要松懈一口气，你也会变穷，而松懈一口气几乎是毫无费力的，这正是一切的趋势，因为每一个人都希望尽可能省力！

  我们假设已经存在的财富不会消亡，不会销毁，那么一部分穷人松懈导致的他们主动放弃的财富便会被动的转移到另一部分稍微努力一点的人手中，造成最初的不均衡。有人会问，为什么会有努力的人，大家难道不能一起松懈吗？

  这个问题很好。我这里的假设是基于正态分布统计的，我的假设是大部分人都维持现状，然后少部分人松懈，少部分人努力一点点。但是要知道，这个正态分布只是一个瞬间量，因为松懈毫不费力，致富需要努力这个原因，松懈的人越来越多。

  但是富人却不会越来越多，而是已经富的人会越来越富。这是一个一将功成万骨枯的模型，而不是集体大生产的模型。这是为什么？因为起初致富的那一小戳人是起初松懈的那一小撮人造就的，然而他们却为自己增加了一点点正能量，这个比别人多了一点的能量可以让他们获取穷人放弃的财富时更占先机，显然，这是一个递归滚雪球的过程，这个过程可以定性地解释马太效应的成因。

财富是一个低熵体，必然要注入能量而产生或者拥有，这是一个费力做功的过程。

---

好吧，我承认，如果我真的相信了我自己在上面扯的那一通，那么在人类文明已经持续进化了7000年左右的今天，我将大概率是一个一无所有的人，你也一样，财富几乎会被个位数的人占据，我们所有人几乎都是奴隶…确实如此，在3000以前，确实是这样，摩西的出埃及就是在这种背景下发生的，后来的赫梯，亚述，波斯，罗马共和国，希腊这些都是这样。但是现在，我们发现不再是这样，至少对于我个人而言，虽然我也经常松懈而不努力，但我过得还不错，难道我上面的论述错了吗？

  还是那个缘由，世界不是一种因素主导的。当初认为工业资产阶级一定会被经济危机摧毁的那些理论家忽略了一个事实，那就是工厂出产的所谓可以成为过剩产品的东西有一个巨大的消费群体，那就是工人本身，如果工厂主知道这个事实，就会给工人适当加薪，用这些薪水去买自己出品的东西…你和我之所以过的不错，正因为此。

  互联网外卖很风靡，但是其重要的消费群体正是互联网行业的人，美团，饿了么的员工自己也点外卖…我们把自己上班做出来的东西卖给了汽车厂的员工，然后我们却买了他们生产的汽车…遍身罗绮者，不是养蚕人的时代已经过去了，在群体看来，自产自销才是根本。

  自产自销确实能维持社会低熵体的持续低成本转动，里面就好像有一个涡轮增压系统。理想情况下，如果能形成一条咬尾蛇就更棒了，这条蛇不断把吞掉自己的身体，不断长胖…

  还有一个问题没有解释，如果那个黑色圆点达到了最右下端会怎样？…省略几万字…会发生类似法国1789年的事情，其实不到那个点就发生了，然后会怎样？然后会再度从新的完全公平线重新开始，直到永远！新的理论来了：

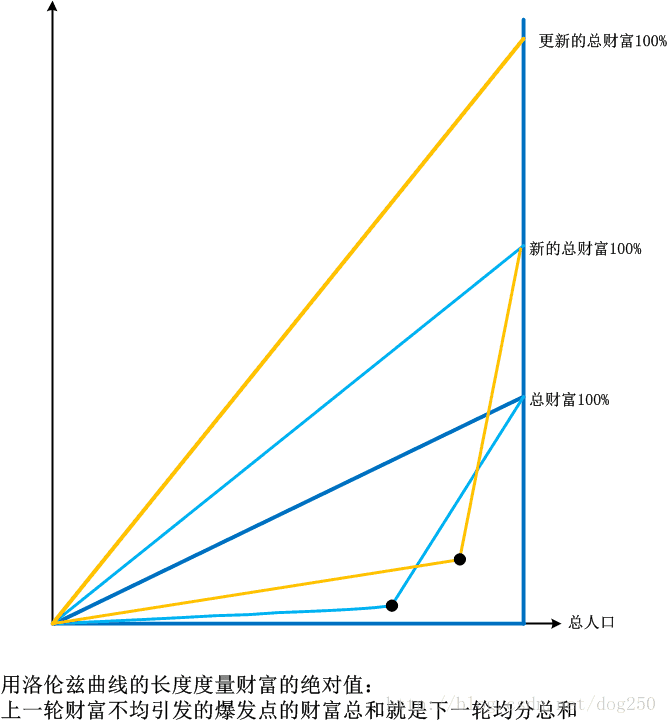
上述图示中，相同颜色的曲线长度相同。

  人口不变的情况下，总的财富会增加，当不公平程度达到极限时，总的财富就会被主动重新分配，然后整体上就会被动重新达到新的不公平极限。我们的世界就是这么发展下去不断达到新的高度的。

---

正态分布和马太效应

马太效应真的是一个普遍现象，不然它不会在两千年前的《马太福音》里出现。古典著作里描绘的几乎都是当时的社会现状，而不是什么神的预言或者箴言，借由神的口吻表达而已，以争取信众。这就好比那些脱口秀演员们口中的“我有一个朋友…”那般。

  文章要结束了，我还是有一个问题搞不懂，为什么自然界包括社会上的很多现象都有马太效应呢？正式一点说，为什么幂律是普遍现象呢？

  其实，正态分布也是普遍现象，我们等车的时候，我们统计身高体重的时候，在预估自己会不会得癌症的时候…但是往往这都不会引起我们的关注，反而针对幂律，我们时刻关注自己是不是处在那个长尾的部分…这很有意思。

  大体上来讲，我觉得独立事件往往遵循正态分布，而相关事件则遵循幂律。身高就是一个独立事件，同班同学里具有血缘关系的情况几乎可以忽略，每一个人都是独立的个体，谁也不影响谁，因此班级里的同学的身高就是正态分布。而收入则不是这样，你在去某家公司，或者决定追随某人时，肯定要先看看这个公司或者个人有没有被别人追随过，从而选取被追随的最多的公司或者个人，以最大限度用别人的时间来降低自己的风险，这就是为什么大家都喜欢去大公司比如BAT上班的原因。也正因为此，在魏晋南北朝前期，五胡乱华，很多汉人都躲进了坞堡，因此也就成全了很多豪族，这些豪族正是后面隋唐时期建设国威的中流砥柱，直到宋朝其财富才被平均。

---

时间，空间，幂律，正态分布

时间换空间

最大限度利用别人在时间维度上的经验来降低自己在瞬间空间选择上的风险，这是一个典型的模式，该模式也许就是非独立事件形成幂律的成因，因为该模式把时间和空间耦合了。

  其实把时间和空间作为对等的维度展开，我们可以发现最终的幂律是不存在的，一切都是正态分布。之所以有些分布看起来是幂律，那是因为时间维度被压缩了，实际上，换句话说，幂律只是空间维度上的说法。

  当我们说80%的财富集中在20%人手中的时候，我们隐含的意思是“当下，现在这个时候”，如果我们把时间维度也算进去，就可以发现，富人积累财富的时间要远远大于穷人放弃财富的时间，按照时间展开，富人的财富会被拉伸，也就是说，在总的时间段看来，并没有穷人和富人之间的关于财富的幂律分布。

  同样的理论可以解释为什么欧洲在近代率先提出了国债而中国没有，原因就是欧洲用时间换了空间，欧洲税率一直都很高，因为它们的国家都很小，为了支付昂贵的列国战争开销并保持自己的稳定，税率很难进一步提高，只能在时间上做文章，即在同一时间点征收未来几年的税并支付时间成本换算成货币后的利息，这就是国债的本质。然而在中国，庞大的领土可以在空间上展的很开，即便是巨额的税收，分摊到这么大的空间内，每一部分也不会太多，这是一个典型的时间/空间不对称压缩的例子。事实上，普遍存在的借钱给利息，期货之类的，都包含了类似的意思。

---

下面一篇文章，我将用我上面的这个模型来解释一下为什么世界的精彩来自精英的创造这件事。
…
  
去年元夜时，花市灯如昼。
月上柳梢头，人约黄昏后。
今年元夜时，月与灯依旧。
不见去年人，泪湿春衫袖。