机器学习模型评价与选择
模型评估的作用
从已训练得到的多个模型中挑选出较好的模型。
以下假设为二分类问题,设样本集为D,分类器为f
评价一:错误率与精度
评价模型好坏,一个最直观的想法就是看它分对或分错的比例,即准确率与错误率。
准确率: acc(f,D)=1m∑I(g(xi)=yi) a c c ( f , D ) = 1 m ∑ I ( g ( x i ) = y i )
错误率: err(f,D)=1m∑I(g(xi)≠yi) e r r ( f , D ) = 1 m ∑ I ( g ( x i ) ≠ y i )
显然,在这种评价下,我们认为准确率高的模型更好一点。
但是,光有准确率似乎不足以解决一些特定问题。比如,在信息检索中,我们可能关心“检索处的信息中有多少是用户感兴趣的”,以及“多少用户感兴趣的信息被检索出来了”,所以有了以下评价
评价二:查准率(precision),查全率(recall),F1
混淆矩阵是模型评价里经常出现的一个概念,如下:
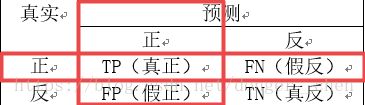
查准率 P=TPTP+FP P = T P T P + F P ,即纵向的准确率
查全率 R=TPTP+FN R = T P T P + F N ,即横向的准确率
通常情况下,这是一对矛盾的度量。因为,假如某个用户在网上检索信息,把整个互联网内容直接扔给TA肯定不会漏掉内容,这时的查全率就很高,用户感兴趣的内容都被我们查到了;但是从另一个角度,查准率就很低了,因为用户对整个互联网信息感兴趣的部分是很小的,即检索出来的信息中用户感兴趣的比例很低。从公式的角度讲,查全就是,如果尽可能让预测为正这样漏掉的可能性就低了,即TP+FP要尽量大,这导致了查准率P下降了;而查准就是使预测的正例是经过深思熟虑的,保证每个给出的信息都是用户感兴趣的,那么漏掉的可能性就大了,TP+FN也会大(因为TP+FN+FP+TN固定)。当然,这不严谨,只是粗糙说明。
查准率-查全率图(P-R)
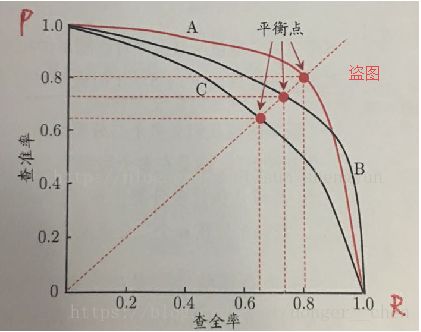
p-r曲线图反应的是查准率与查全率的关系
绘制方法是:
1.根据分类器给所有样本一个分为正例的概率
2.按照概率将样本从大到小排序
3.对排序后的数据集进行切分,左边的样本当正例,右边的样本当反 例,然后计算R和P。从数据集左端开始切分,每切 一刀,计算一次R和P,切m+1次 就可得出P-R曲线
怎么通过P-R曲线图看模型的好坏呢?显然,查准率和查全率都高的模型自然是较好的如B曲线的点都高过C曲线,则可说B模型比C模型好。但是,通常会出现交叉的情况,即A与B曲线的情况,用上述方式就难以判断了。换种思路,查准率和查全率越高,那么p-r曲线所围成的面积不也越大吗?这样通过比较曲线下面积的大小就是一种衡量方式。遗憾的是,这个面积算起来较麻烦,退而求其次,就引出了“平衡点”(BEP)的概念,它指的是P=R时的取值,就是如图所示的红点,这样就有A>B>C的结论。但但但,学者们认为,BEP过于简化了,然后就有了F1度量,它是P和R的调和平均
有时候更近一步,采用加权调和平均
在进行多次训练得到多个混淆矩阵的情况下,可对P,R采用平均的方式计算。
评价三:ROC与AUC
如果分类器给出的预测结果是一个实数值或概率,我们通常给定一个阈值,大于阈值的定为正例,小于阈值的定为反例,如logistic回归或神经网络等。
如果我们像绘制P-R曲线时根据预测结果从大到小把样本排序,但重新定义两个变量真正例率TPR,假正例率FPR
TPR=TPTP+FN T P R = T P T P + F N , FPR=FPFP+TN F P R = F P F P + T N
ROC曲线的绘制:
1.根据预测结果从大到小把样本排序
2.将阈值从大到小调节,每更新一次阈值,计算一次TPR和FPR
3.绘制得到的所有点对(TPR,FPR)
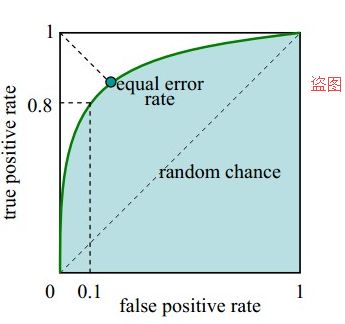
曲线越靠近左上角说明泛化能力越好,到达(0,1)点即为完美模型。在ROC中,比较两个模型好坏依然会存在曲线交叉问题,因此采用曲线形面积(AUC)来比较,AUC越大,模型泛化能力越好。
评价四:代价敏感错误率与代价曲线
代价敏感产生于不同错误所造成的后果不同。比如,在医疗诊断中,把没病的人误诊为生病跟把生病的人误诊为没病的后果是完全不同的。为了平衡这点,我们在模型训练时对正样例与负样例给予不同的损失。

根据犯两种错误的不同程度后果,通过调节cost1与cost2的比例来平衡。
设样本为正例的集合为D+,样本为反例的集合为D-
代价敏感错误率定义为
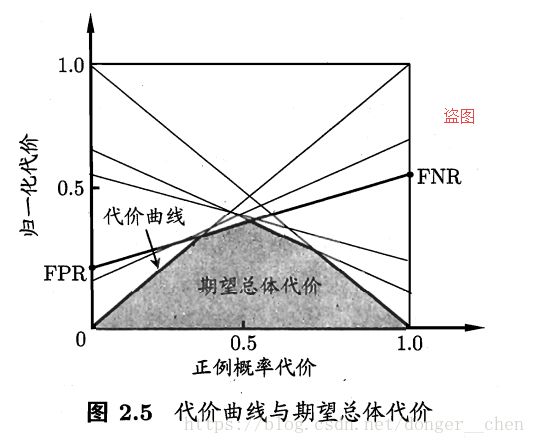
ROC曲线不能反应非均等代价下分类器的好坏,这时需要借助代价曲线
定义正概率代价
p是样例为正的概率
再定义
代价敏感曲线的绘制:
1.选取ROC曲线上的一点(TPR,FPR),计算FNR
2.绘制一条从(0,FPR)到(1,FNR)的线段,线段下面积的意义是:该条件下期望的总体代价
3.取遍ROC上的每一点,重复2
4.取所有线段的下界,即为代价曲线
参考:周志华. 机器学习 : = Machine learning[M]. 清华大学出版社, 2016.