【NOI2014模拟7.11】数学题
Description
Solution
这题是一道很奇妙的题目。
首先在共线或者夹角非常小的时候,答案是 gcd(|X|,|Y|) ,那么考虑一下,是否和gcd有关。
明显很难有关系,但是这种思想很重要类欧几里得算法,考虑把(X,Y)这个向量转化成(X’,Y’)这个向量。
首先需要的是边界条件。
我们可以知道在θ大于60°的时候,答案为min(|X|,|Y|)。
设X=(c,0),Y=(e,f),设 |X|≤|Y|
证明: |aX+bY|=(c+e)2+f2−−−−−−−−−−√=c2+e2+2ce+f2−−−−−−−−−−−−−−−√
=|aX|2+|bY|2+2cosθ|aX||bY|−−−−−−−−−−−−−−−−−−−−−−−−√
≥|aX|2+|bY|2−2cosθ|aX||bY|−−−−−−−−−−−−−−−−−−−−−−−−√
当 2cosθ≤1的时候
≥|aX|2+|bY|2−|aX||bY|−−−−−−−−−−−−−−−−−−−√
≥(|aX|−|bY|)2+|aX||bY|−−−−−−−−−−−−−−−−−−−−√
所以显然在|X|=0或|Y|=0答案只会≥|X|。
否则无论a,b取什么值(不能同时=0)|aX||bY|≥|X|
所以得证:边界是θ≥60°的时候,ans=|X|(如果|X|>|Y|那么交换),就是前面的系数是(1,0)。
那么现在的关键就是要把角度不断的变大。
首先考虑如何正确的转化(X,Y)。
|aX+bY|=|aX−akY+bY+akY|=|a(X−kY)+(b+ak)Y|
就是说向量(X,Y)和向量(X-kY,Y)的答案是等价的,可以互相转化,但是系数不同,前者是(a,b),后者是(a,b+ak)。
那么我们现在要考虑k=?的时候,角度可以变大。
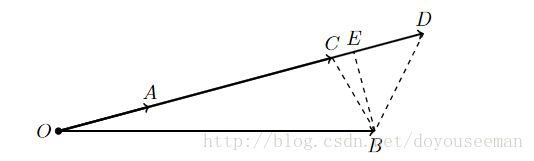
设OC=kX,BE⊥OD,OD=(k+1)X,OA=X,OB=Y。
当E落在OA上的时候,此时显然有角OAB>角AOB,那么可以把(X,Y)转化成(Y,X)=>(Y-X,X)(k=1)及(OB-OA,OA)及(AB,OA)。此时是可以把角度变大的。
当E落在OA外的时候:
1、当|CE|>|ED|时就取较大的角ODB及转化为
(OA,OB)=>(OB,OA)=>(OB-(k+1)OA,OA)=>(DB,OA)
2、否则取较大的角DBC及转化为
(OA,OB)=>(OB,OA)=>(OB-kOA,OA)=>(CB,OA)
此时注意(a,b)系数转化完之后的变化。
其实不用特殊考虑E落在OA外的时候,第二种情况可以顺便考虑进去及(Y-(k+1)X,X)落在里面是k=0,及(Y-X,X)。
还要考虑的细节:
1、角度的判断用向量的点积。
2、当角度>90°时,及点积<0,此时(X,Y)转化为(X,-Y),对应的系数也要变成(a,-b)
3、求k的时候可以直接用点积整除以(X的模长的平方)
证明:
OE=|Y|cosθ,⌊OE|X|⌋=⌊|Y|cosθ|X|⌋=k
X=(x1,y1),Y=x2,y2
|X||Y|cosθ=x1x2+y1y2(点积)
所以 |Y|cosθ=x1x2+y1y2|Y|
所以 ⌊x1x2+y1y2|X|2⌋=k
Code
#include*bmo|!amo){
a=1,b=0;
return;
}
ll k=ji/amo;
if(2*ji>(2*k+1)*amo){
leiou(a,b,x,y,xx-(k+1)*x,yy-(k+1)*y);
a-=(k+1)*b;
}
else{
leiou(a,b,x,y,xx-k*x,yy-k*y);
a-=k*b;
}
}
int main(){
// freopen("math.in","r",stdin);
// freopen("math.out","w",stdout);
freopen("fan.in","r",stdin);
freopen("fan.out","w",stdout);
while(scanf("%lld%lld%lld%lld",&x,&y,&xx,&yy)!=EOF){
leiou(a,b,x,y,xx,yy);
printf("%lld\n",sqr(a*x+b*xx)+sqr(a*y+b*yy));
}
} 