app2vec在广告投放中的应用
本文参考了important_MODELING USERS FOR ONLINE ADVERTISING,主要介绍word2vec的改进版本app2vec在广告投放系统中的应用。
一、word2vec
原理部分不再叙述,下面先回顾一下word2vec在求word embedding的过程,以CBOW为例
假如我们现在有一段文本{I drink coffee everyday},一共包含五个四个单词,选择coffee为中心词window size设为2
也就是说,我们要根据单词"I","drink"和"everyday"来预测一个单词,并且我们希望这个单词是coffee。
每个单词的onehot表示如下
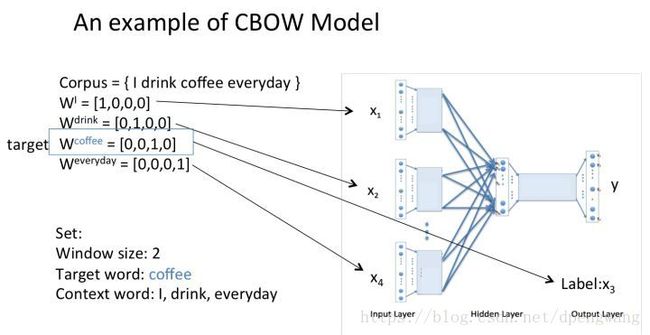
W矩阵是我们最终需要的embedding矩阵,也被称为look up table,用该矩阵乘以单词的onehot编码就能得到某个单词的embedding,很好理解,矩阵shape为vN,v是一个单词的embedding后的长度,N是单词的数目,onehot编码为N1,Wonehot = v1 大小的word embedding
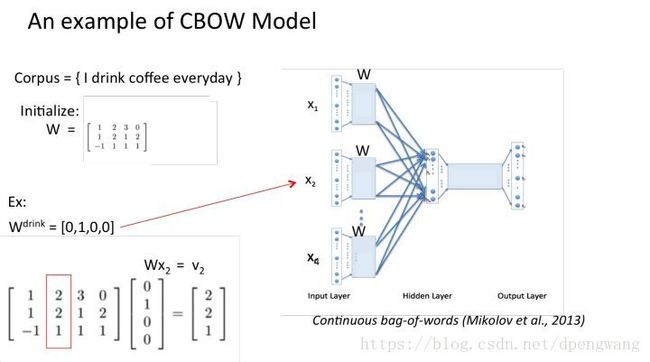
当我们用coffee的上下文中的三个单词(I drink eveyday)去预测coffee时,我们会通过W矩阵乘以这个三个单词的onehot编码得到这三个单词的word embedding ,并将它们取平均得到u^
(这里为什么取平均,取平均是个经验做法,在论文里用的就是取平均的方法,可能word2vec的作者尝试了其他不同的做法后觉得取平均是一种最好的方法
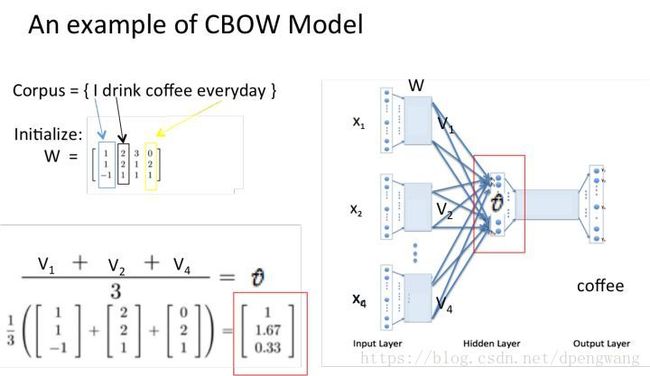
得到了上下文的embedding 的平均值后(shape 为v*1),与权重矩阵W’相乘得到一个向量U0 ,U0 =W’ * v ˉ \bar{v} vˉ(shape 为N *1)
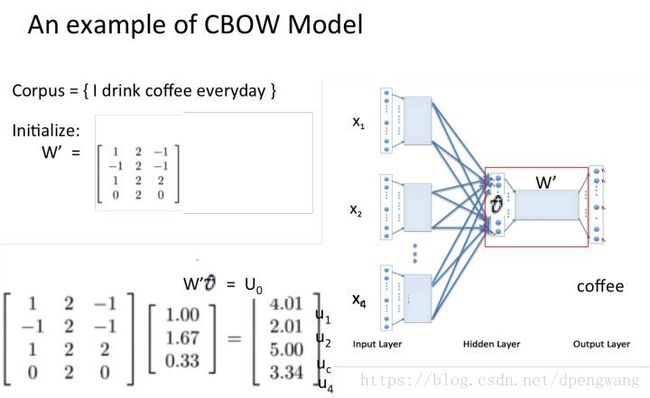
对U0 进行softmax处理,得到一个N *1的概率向量
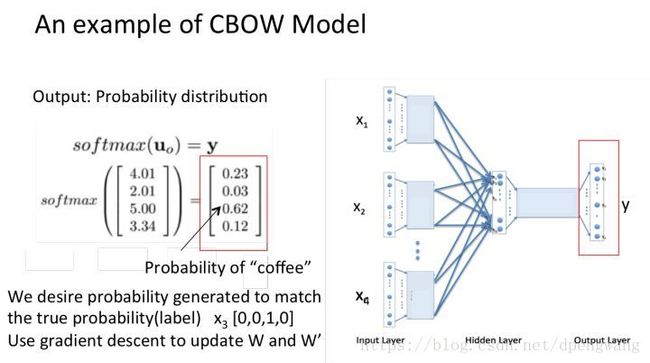
我们希望y在第三个值上的概率为1(因为coffee的onehot编码在为[0,0,1,0]T),而现在对应位置的值不是1而是0.62.就这样将误差进行反向传播,不断的更新矩阵W和矩阵W’直到满足条件为止(W是最终我们需要得到的embedding矩阵,而W’权重矩阵是副产物)
下面来说明如何softmax是如何计算概率分布的
P ( w t ∣ w t − c : w t + c ) = e x p ( v ˉ T v w t ′ ) ∑ w = 1 W e x p ( v ˉ T v w ′ ) P(w_{t}|w_{t-c}:w_{t+c}) =\frac{exp(\bar{v}^Tv^{'}_{w_{t}})}{\sum_{w=1}^{W}exp(\bar{v}^{T} v^{'}_{w})} P(wt∣wt−c:wt+c)=∑w=1Wexp(vˉTvw′)exp(vˉTvwt′)
其中
v ˉ = 1 2 c ∑ − c ≤ j ≤ c , j ≠ 0 v j \bar{v} = \frac{1}{2c} \sum_{-c\leq j\leq c,j\neq 0}^{ }v_{j} vˉ=2c1−c≤j≤c,j̸=0∑vj
可以看到,在计算softmax的时候, v ˉ \bar{v} vˉ是通过对上下文的word embedding 向量求平均得到的,也就是说,他把上下文中的所有单词看成是均等的,这一定程度上就丢失了很多信息(接下来要介绍的app2vec就是对此的改进)
二、app2vec
上面我们已经了解了word2vec求word embedding 的过程,接下来介绍word2vec的改进版本app2vec。
app2vec目的在于将app 进行embedding,将app embedding的方法有很多,比如传统的word2vec模型,将app的title description、market categories 以及user reviews等等信息作为document 放到word2vec模型中进行训练得到app对应的向量,也可以通过矩阵分解的方式得到app的向量,在这里就不介绍了。
对于某个用户,他在一段时间内的app使用情况如下:
(A, t 1 , A, t 2 , A, t 3 , B, t 4 , C, t 5 , A)
也就是说用户用完app A后,隔了t1时间段后又使用了A,隔了t2时间段后又使用了A,隔了t3时间段后又使用了B,隔了t4时间段后又使用了C,隔了t5时间段后又使用了A,如此类推
我们去重后得到如下的序列
(A,t 3 ,B,t 4 ,C,t 5 ,A)
我们 可以认为,时间使用时间越小的两个app之间,他们对应的app embedding 相似性越大,也就是说在word2vec模型训练的过程总,上下文中的某些app对将要预测的app贡献越大,我们用如下公式来衡量两个app之间的相似性,wi 和wt分别代表两个app,l表示两个app之间的使用间隔(以分做单位), α \alpha α取经验值0.8
r ( w i , w t ) = α l r(w_{i},w_{t}) = \alpha ^{l} r(wi,wt)=αl
在word2vec的softmax求值公式中,我们将 v ˉ \bar{v} vˉ原来的公式
v ˉ = 1 2 c ∑ − c ≤ j ≤ c , j ≠ 0 v j \bar{v} = \frac{1}{2c} \sum_{-c\leq j\leq c,j\neq 0}^{ }v_{j} vˉ=2c1−c≤j≤c,j̸=0∑vj
修改为
v ˉ = ∑ − c ≤ j ≤ c , j ≠ 0 r ( w i w j ) v j ∑ − c ≤ j ≤ c , j ≠ 0 r ( w i w j ) \bar{v}=\frac{\sum_{-c\leq j\leq c ,j\neq 0}^{ } r(w_{i}w_{j})v_{j}}{\sum_{-c\leq j\leq c ,j\neq 0}^{ } r(w_{i}w_{j})} vˉ=∑−c≤j≤c,j̸=0r(wiwj)∑−c≤j≤c,j̸=0r(wiwj)vj
这样 ,就改善了word2vec中上下文中单词对预测单词贡献等价的缺点,通过改进后的word2vec模型训练得到的word embedding 更加具有个性化,更适合用于推荐系统
三、基于DPP过程和app2vec的广告投放
广告投放就是对于指定的用户投放对应的广告,推荐系统的应用之一,传统的推荐系统有基于user-item,有基于item-user以及奇异矩阵分解的,核心在于求出item或者user对应的embedding向量,然后利用类如余弦相似性等计算距离的手段来进行推荐,下面我们来介绍一种通过DPP过程来进行推荐的方法。
什么是DPP
DPP过程是一种物理学中描述分子间作用力的过程,如果一个集合满足是DPP过程,那么从该集合中取出若干个元素的概率满足如下公式
P L ( Y ) = d e t ( L Y ) ∑ Y ′ ϵ Γ d e t ( L Y ′ ) P_{L}(Y) = \frac{det(L_{Y})}{\sum_{Y^{'}\epsilon \Gamma }^{ }det(L_{Y^{'}})} PL(Y)=∑Y′ϵΓdet(LY′)det(LY)
等式右边分子表示集合Y中元素组成的行列式的值,集合中元素是如何组成矩阵的呢,请看如下解释
在DPP过程中的,K为一个相似矩阵,比如集合Y中有4个元素,那么矩阵中[1,2]坐标的元素表示的元素1和元素2的相似度,相似度怎么计算得到的呢,就是利用之前的app2vec得到的,每个元素我们都可以使用embedding来表示,然后通过余弦相似性计算两个向量之间的相似性即可。
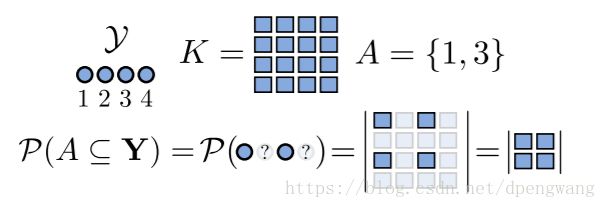
如果要从矩阵中取出集合A{1,3},那么对应的矩阵所包含的元素就是([1,1],[3,3],[3,1],[3,3])(以此类推)
DPP过程就是从集合里选出最与众不同的若干个元素
基于DPP的推荐系统
应用场景:当我们拥有用户的app使用情况时,我们如何才能尽可能的将我们的广告投放到用户使用的不同类别的app上(比如我们想让广告尽可能的分散到不同类别的app上)
首先定义某个app的重要性q(a,u),即app a对于用户u的重要性,并且用该app与用户u使用过的所有app的相似性之和的平均值作为衡量标准。
定义如下公式
q ( a , u ) = 1 n ∑ i = 1 n s i m ( a , A i ) q(a,u)=\frac{1}{n}\sum_{i=1}^{n}sim(a,A_{i}) q(a,u)=n1i=1∑nsim(a,Ai)
这样我们就能计算出用户使用的每个app对于用户的重要性q(a,u)
定义如下符号
- ϕ i \phi _{i} ϕi是归一化后的表示app 的向量,所以 ϕ i T ϕ j ϵ [ − 1 , 1 ] \phi _{i}^{T}\phi _{j} \epsilon[-1,1] ϕiTϕjϵ[−1,1]
- q i q _{i} qi为app i 的重要性
- L i , j = q i ϕ i T ϕ j q j L_{i,j}=q_{i}\phi _{i}^{T}\phi _{j}q_{j} Li,j=qiϕiTϕjqj
- S i , j = L i , j L i , i L j , j S_{i,j} = \frac{L_{i,j}}{\sqrt{L_{i,i}L_{j,j}}} Si,j=Li,iLj,jLi,j
定义了如上的表达式后,我们就能将之前的DPP表达式中的分母
P L ( Y ) = d e t ( L Y ) ∑ Y ′ ϵ Γ d e t ( L Y ′ ) P_{L}(Y) = \frac{det(L_{Y})}{\sum_{Y^{'}\epsilon \Gamma }^{ }det(L_{Y^{'}})} PL(Y)=∑Y′ϵΓdet(LY′)det(LY)
修改为
P L ( Y ) = ( ∏ i ϵ Y q i 2 ) d e t ( S Y ) P_{L}(Y)=(\prod_{i\epsilon Y}^{ }q_{i}^2)det(S_{Y}) PL(Y)=(iϵY∏qi2)det(SY)
这样,我们从候选集中选取元素时,不仅考虑了多样性,也考虑的重要性。
K-DPP
在实际应用过程中,我们从候选的广告集中选取广告数目一般是指定的,我们将DPP算法限定为K-DPP算法,并通过以下面的贪心算法来从一个满足DPP过程的候选集中选取K个元素

算法很容易理解,候选集为U,目标集合为Y,每次从U中选取一个元素,使得选取的元素与Y中已有的元素组成的DPP矩阵的 l o g d e t ( L Y ) logdet(L_{Y}) logdet(LY)值最大,重复此过程知道Y中的元素个数为K停止。
四、总结
传统的word2vec模型在求词向量是忽略了上下文中词与词之间的关联性,而app2vec对word2vec进行了改进,将用的使用app的时间间隔作为相关因子,训练出具有用户个性化的word embedding。为了达到将广告尽可能的投放到多样的并且重要的app中,使用DPP过程加以实现,DPP中使用的相似矩阵以及app对于用户的重要性都是通过由app2vec模型训练得到的word emdedding 来计算得到的。
参考资料:
modeling users for online advertising
word2vec
Determinantal point processes for machine learning