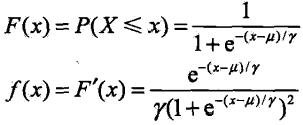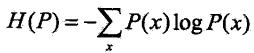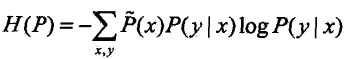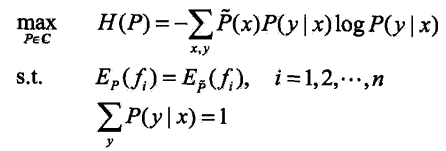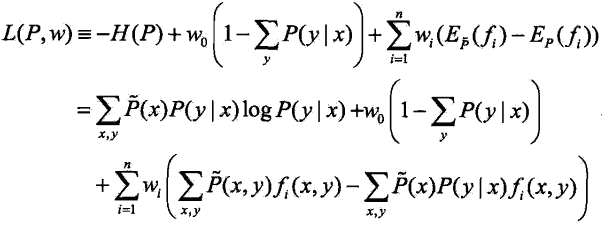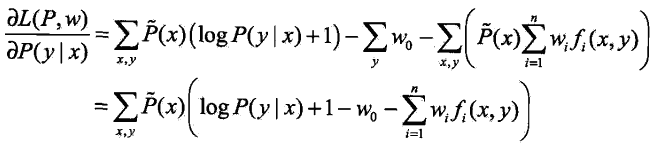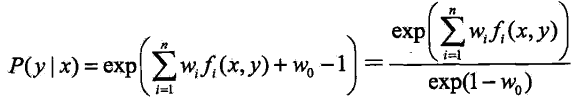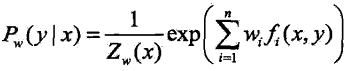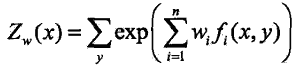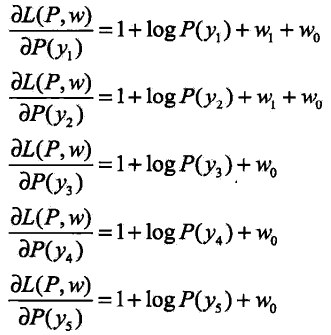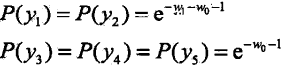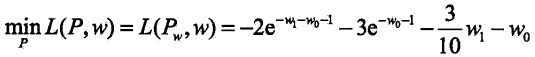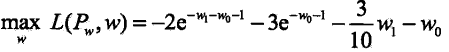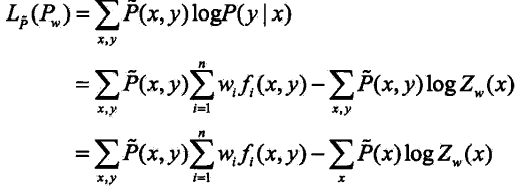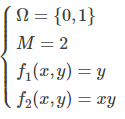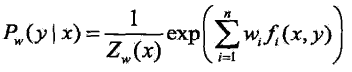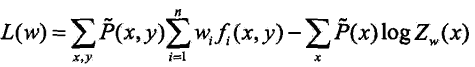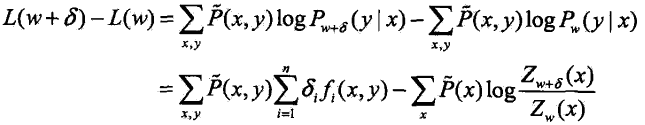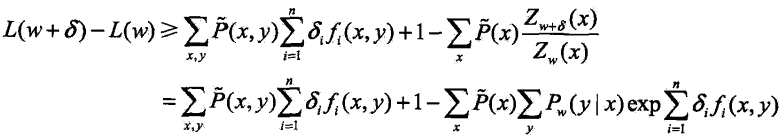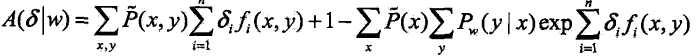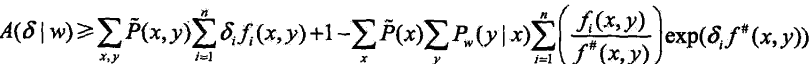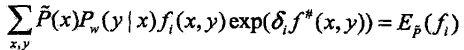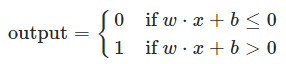逻辑斯蒂回归与最大熵模型初探

1. 算法概述

0x1：逻辑斯蒂回归

逻辑斯蒂回归（logistic regression）是统计学习中的经典分类方法，它属于一种对数线性模型（转化为对数形式后可转化为线性模型）

从概率角度看，逻辑斯蒂回归本质上是给定特征条件下的类别条件概率

0x2：最大熵准则

最大熵模型的原则：

承认已知事物（知识）；
对未知事物不做任何假设，没有任何偏见。

对一个随机事件的概率分布进行预测时，我们的预测应当满足全部已知条件，而对未知的情况不要做任何主观假设。在这种情况下，概率分布最均匀，预测的风险最小。

因为这时概率分布的信息熵最大，所以人们把这种模型叫做“最大熵模型”（Maximum Entropy）

0x3：逻辑斯蒂回归和深度神经网络DNN的关系

逻辑斯蒂回归模型中的sigmoid函数输出是一个概率置信度，我们把单层逻辑斯蒂回归的条件概率输出直接进行argmax判断就是传统逻辑斯蒂回归模型，如果stacking层层堆叠起来，就成为了一个人工神经网络

Relevant Link:

https://www.cnblogs.com/little-YTMM/p/5582271.html

 

1. 逻辑斯蒂回归模型

0x1：逻辑斯蒂分布（logistic distribution）

设 X 是随机变量，X 服从逻辑斯蒂分布是指 X 具有下列分布函数和密度函数

式中，为位置参数，为形状参数

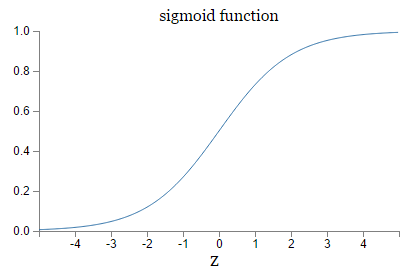
逻辑斯蒂回归密度函数；和分布函数图形如下图所示

分布函数属于逻辑斯蒂函数，其图形是一条S形曲线（sigmoiid curve），该曲线以点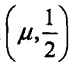为中心对称

曲线在中心附近增长变化较快，在两端增长变化较慢。形状参数越小，sigmoid曲线在中心附近增长得越快

0x2：二项逻辑斯蒂回归模型 - 二分类

二项逻辑斯蒂回归模型（binominal logistic regression model）是一种分类模型，由条件概率分布表示，形式为参数化（概率离散化）的逻辑斯蒂分布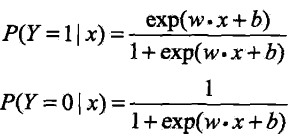

对于给定的输入实例 x，按照上式可以得到和。二项逻辑斯蒂回归比较两个条件概率值的大小（类似朴素贝叶斯的最大后验概率比较），将实例 x 分到概率较大的那一类

1. 借助二项逻辑斯蒂回归来验证一个论断：逻辑斯蒂回归是对数线性模型

我们来考察一下逻辑斯蒂回归模型的特点。一个事件的几率（odds）是指该事件发生的概率与该事件不发生的概率的比值，对二项逻辑斯蒂回归而言，几率公式为：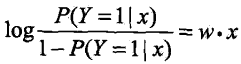

这就是说，在逻辑斯蒂回归模型中，输出 Y = 1的对数几率是输入 x 的线性函数，或者说，输出 Y = 1的对数几率是由输入 x 的线性函数表示的模型，即逻辑斯蒂回归模型

值得注意的是，这个论断对多项情况下也是成立的，只是证明更复杂一些

0x3：多项式逻辑斯蒂回归模型 - 多分类

多项式逻辑斯蒂回归模型（multi-norminal logistic regression model）用于多分类。设离散型随机变量 Y 的取值集合是｛1，2，....，K｝，那么多项逻辑斯蒂回归模型是：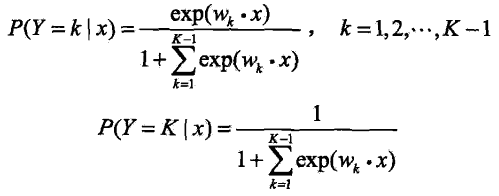

 

2. 最大熵模型

0x1： 最大熵原理

最大熵原理是概率模型中的一个准则。最大熵原理认为，学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。通常用约束条件来确定概率模型的集合，所以最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型

假设离散随机变量 X 的概率分布是 P（X），则其熵为：

熵满足下列不等式：，式中是 X 的取值个数，当且仅当 X 的分布是均匀分布时右边的等号成立，也即当 X 服从均匀分布时，熵最大

直观上说：

最大熵原理认为要选择的概率模型首先必须满足已有的事实，即约束条件，在没有更多信息的情况下，那些不确定的部分都是"等可能的"。最大熵原理通过熵的最大化来表示等可能性，因为"等可能"不容易工程化，而熵则是一个可优化的数值指标

1. 用一个例子来说明最大熵原理

假设随机变量 X 有5个取值｛A，B，C，D，E｝，要估计各个取值的概率

解：这些概率满足以下约束条件：

但问题是，满足这个约束条件的概率分布有无穷多个，如果没有任何其他信息，要对概率分布进行估计，一个办法就是认为这个分布中的各个取值是等概率的：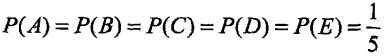

等概率表示了对事实的无知，因为没有更多的信息，这种判断是合理的。

但是有时，能从一些先验知识中得到一些对概率值的约束条件，例如：

满足这两个约束条件的概率分布仍然有无穷多个，在缺失其他信息的情况下，可以继续使用最大熵原则，即：

我们在朴素贝叶斯法的最大似然估计中，在没有明确先验知识的情况下，对先验概率设定等概率分布（即熵值最大）的做法就是符合"最大熵原理"的一种做法。但是在参数估计前如果对先验分布有一定的知识，就可以变成MAP估计

0x2：最大熵模型的定义

最大熵原理是统计学习的一般原理，将它应用到分类得到最大熵模型。假设分类模型是一个条件概率分布，表示给定的输入Ｘ，以条件概率输出Ｙ

给定一个训练数据集：

学习的目标是用最大熵原理选择最好的分类模型。

我们先来定义约束条件，即：

特征函数关于经验分布的期望值（从样本中估计），与，特征函数关于模型与经验分布的期望值。如果模型能够获取训练数据中的信息，那么就可以假设这两个期望相等：

我们将上式作为模型学习的约束条件，加入有 n 个特征函数

，那么就有 n 个约束条件

1. 最大熵模型数学定义

 假设满足左右约束条件的模型集合为：

定义在条件概率分布上的条件熵为：

则模型集合C中条件熵最大的模型成为最大熵模型

 

3. 逻辑斯蒂回归模型及最大熵模型策略

0x1：约束最优化问题 - 解决最大熵模型空间的搜索问题

最大熵模型的学习过程就是求解最大熵模型的过程，最大熵模型的学习可以形式化为约束最优化问题

对于给定的训练数据集以及特征函数，最大熵模型的学习等价于约束最优化问题：

按照对偶等价的思想，将求最大值问题改写为等价的求最小值问题：

求解上式约束最优化问题所得出的解，就是最大熵模型学习的解。下面进行一个推导

将约束最优化问题的原始问题转换为无约束最优化的对偶问题，通过解对偶问题求解原始问题。首先，引进拉格朗日乘子w0，w1，...，wn，定义拉格朗日函数：L（P，w）

最优化的原始问题是：

对偶问题是：

首先，求解对偶问题内部的极小化问题：，它是 w 的函数，将其记作：，称为对偶函数。同时，将其解记作：

具体地，求对的偏导数：

令偏导数等于0，在的情况下，解得：

由于，得

，其中：

称为规范化因子；是特征函数；是特征的权值。上二式表示的就是最大熵模型，这里 w 是最大熵模型中的参数向量

之后，求解对偶问题外部的极大化问题：，将其解记为，即

1. 用一个例子来说明最大熵原理

文章上面我们通过直接应用最大熵原理和直观上的直觉解决了一个在有限约束下的模型参数估计问题，这里我们继续运用拉格朗日乘子法求解约束最优化的思想再次求解该问题

分别以y1，y2，y3，y4，y5表示A，B，C，D，E。于是最大熵模型学习的最优化问题是：

引进拉格朗日乘子w0，w1，定义拉格朗日函数：

根据拉格朗日对偶性，可以通过求解对偶最优化问题得到原始最优化问题的解：

首先求解关于P的极小化问题，为此，固定w1，w1，求偏导数

令各偏导数等于0，解得：

于是：

再求解关于 w 的极大化问题：

分别对w0和w1求偏导数并令其为0，得到：

可以看到，结果和我们直观上理解的是一致的

0x2：最大似然估计 - 经验风险最小化拟合训练样本

上一小节我们看到，最大熵模型是由

和 表示的条件概率分布。

下面我们来证明其对偶函数的极大化等价于最大熵模型的极大似然估计（即最大熵原理和极大似然原理的核心思想是互通的）

已知训练数据的经验概率分布，条件概率分布的对数似然函数表示为：

当条件概率分布是最大熵模型时，对数似然函数为：

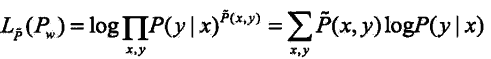
再看条件概率最大熵模型的对偶函数

比较上面两式可得：

即对偶函数等价于对数似然函数，于是证明了最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计这个论断

这样，最大熵模型的学习问题就转换为具体求解对数似然函数极大化或对偶函数极大化的问题

可以将最大熵模型写成更一般的形式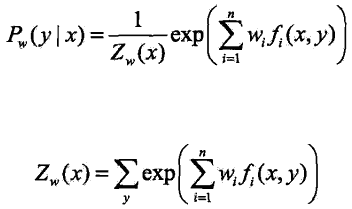：，这里，为任意实值特征函数

0x3：逻辑斯蒂回归与最大熵模型的等价性

最大熵模型与逻辑斯蒂回归模型有类似的形式，它们又称为对数线性模型（log linear model）。

它们在算法策略上也存在共通的形式和思想，模型学习都是在给定的训练数据条件下对模型进行极大似然估计（遵循最大熵原理），或正则化的极大似然估计

在最大熵模型中, 令:

即可得到逻辑斯蒂回归模型.

Relevant Link:

http://blog.csdn.net/foryoundsc/article/details/71374893

 

4. 逻辑斯蒂回归、最大熵算法 - 参数估计

我们既然已经有了最大熵原理和最大似然估计了，不就可以直接得到目标函数（或条件概率）的全局最优解了吗？但是就和决策树学习中一样，最大熵增益原理只是指导思想，具体到工程化实现时还需要有一个高效快捷的方法来求得"最佳参数"

逻辑斯蒂回归模型、最大熵模型学习归结为以似然函数为目标函数的最优化问题，因为目标函数中包含有大量的乘法项直接求导求极值十分困难，因此通过通过迭代算法求解（这点在深度神经网络中也是一样）。从最优化的观点看，这时的目标函数具有很好的性质，它是光滑的凸函数，因此多种最优化的方法都适用，保证能找到全局最优解，常用的方法有改进的迭代尺度法、梯度下降法、牛顿法、拟牛顿法

0x1：改进的迭代尺度法

改进的迭代尺度法（improved interative scaling IIS）是一种最大熵模型学习的最优化算法。

已知最大熵模型为：

对数似然函数为：

目标是通过极大似然估计学习模型参数，即求对数似然函数的极大值。因为似然函数 = 概率密度（而这里的概率密度函数就是最大熵模型），所以求对数似然函数的极大值就是在求最大熵模型的最优解

IIS的想法是：

假设最大熵模型当前的参数向量是，我们希望找到一个新的参数向量，使得模型的对数似然函数值增大。如果能有这样一种参数向量的更新方法，那么就可以重复使用这一方法，（逐步迭代），直至找到对数似然函数的最大值

对于给定的（本轮迭代）经验分布，模型参数从到，对数似然函数的改变量是：

利用不等式：

建立对数似然函数改变量的下界：

将右端记为：

于是有：

即是对数似然函数本轮迭代改变量的一个下界。如果能找到适当的使下界提高，那么对数似然函数也会提高。

然而，函数中的是一个向量，含有多个变量，不易同时优化。IIS试图一次只优化其中一个变量，而固定其他变量

为达到这一目的，IIS进一步降低下界。具体地，IIS引进一个量

因为是二值函数，故表示所有特征在（x，y）出现的次数，这样，可以改写为：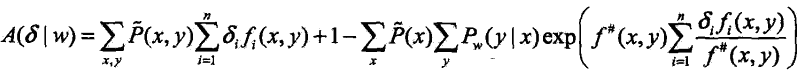

根据Jensen不等式上式可改写为：

记不等式右端为：

于是得到：

这里，是对数似然改变量的一个新的（相对不紧）下界。于是求对的偏导数：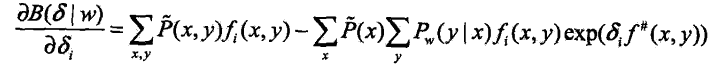

上式中，除了外不包含任何其他变量，令偏导数为0得到：

依次对求解方程可以求出

算法的过程可以参阅下面的python代码实现

 

5. 逻辑斯蒂回归模型和感知机模型的联系与区别讨论

我们知道，感知机模型对输入 x 进行分类的线性函数，其值域（输入）为整个实属域，以一元（1维特征变量）感知机为例，感知机的判别函数实际上是一个阶跃函数

逻辑斯蒂回归模型相当于改进版本的感知机，它在感知机的输出后面加上了一个sigmoid函数，使其概率分布函数增加了一些新的特性

1. f(x;β)∈[0,1].
2. f应该至少是个连续函数. 这是因为我们希望模型f的输出能够随 x平滑地变化.
3. f应该尽可能简单.

sigmoid不仅完成了值域概率化压缩，同时还使概率分布函数连续可导，通过逻辑斯蒂回归模型可以将线性函数转换为概率：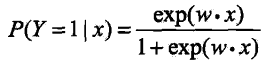

这时，线性函数的值（输入）越接近正无穷，概率值就越接近于1；线性函数的值越接近于负无穷，概率值就越接近于0，即实现了判别结果概率化压缩，这样的模型就是逻辑斯蒂回归模型

 

6. 用Python实现最大熵模型（MNIST数据集） 

0x1：数据地址

https://github.com/LittleHann/lihang_book_algorithm/blob/master/data/train_binary.csv

0x2：code

# -*- coding: utf-8 -*-

import pandas as pd
import numpy as np
import os

import time
import math
import random

from collections import defaultdict

from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score


class MaxEnt(object):

    def init_params(self, X, Y):
        self.X_ = X
        self.Y_ = set()

        # 计算(x, y)和(x)的总数
        self.cal_Pxy_Px(X, Y)

        self.N = len(X)                 # 训练集大小
        self.n = len(self.Pxy)          # 书中(x,y)总数n
        self.M = 10000.0                # 书91页那个M，但实际操作中并没有用那个值
        # 可认为是学习速率

        self.build_dict()

        # 计算特征函数f(x,y)关于经验分布P~(X,Y)的期望值
        self.cal_EPxy()

    def build_dict(self):
        self.id2xy = {}
        self.xy2id = {}

        for i, (x, y) in enumerate(self.Pxy):
            self.id2xy[i] = (x, y)
            self.xy2id[(x, y)] = i

    def cal_Pxy_Px(self, X, Y):
        self.Pxy = defaultdict(int)
        self.Px = defaultdict(int)

        for i in xrange(len(X)):
            x_, y = X[i], Y[i]
            self.Y_.add(y)

            for x in x_:
                self.Pxy[(x, y)] += 1
                self.Px[x] += 1

    def cal_EPxy(self):
        '''
        计算书中82页最下面那个期望
        '''
        self.EPxy = defaultdict(float)
        for id in xrange(self.n):
            (x, y) = self.id2xy[id]
            # 特征函数f(x,y)是0/1指示函数，所以频数/总数 = 概率P(x,y)
            self.EPxy[id] = float(self.Pxy[(x, y)]) / float(self.N)

    def cal_pyx(self, X, y):
        result = 0.0
        for x in X:
            if self.fxy(x, y):
                id = self.xy2id[(x, y)]
                result += self.w[id]
        return (math.exp(result), y)

    def cal_probality(self, X):
        '''
        计算书85页公式6.22
        '''
        # 计算P(Y|X)条件概率
        Pyxs = [(self.cal_pyx(X, y)) for y in self.Y_]
        Z = sum([prob for prob, y in Pyxs])
        return [(prob / Z, y) for prob, y in Pyxs]

    def cal_EPx(self):
        '''
        计算书83页最上面那个期望
        '''
        self.EPx = [0.0 for i in xrange(self.n)]

        for i, X in enumerate(self.X_):
            # 得到P(y|x)条件概率
            Pyxs = self.cal_probality(X)

            for x in X:
                for Pyx, y in Pyxs:
                    if self.fxy(x, y):
                        id = self.xy2id[(x, y)]
                        # 计算特征函数f(x,y)关于模型P(Y|X)与经验分布P~(X)的期望值
                        self.EPx[id] += Pyx * (1.0 / self.N)

    def fxy(self, x, y):
        return (x, y) in self.xy2id

    def train(self, X, Y):
        # 初始化参数，计算一些概率，期望等变量
        self.init_params(X, Y)
        # 初始化每个样本特征函数的权重w = 0
        self.w = [0.0 for i in range(self.n)]

        max_iteration = 50
        for times in xrange(max_iteration):
            print 'iterater times %d' % times
            sigmas = []
            self.cal_EPx()

            for i in xrange(self.n):
                # 书上91页，公式6.34
                sigma = 1 / self.M * math.log(self.EPxy[i] / self.EPx[i])
                sigmas.append(sigma)

            # if len(filter(lambda x: abs(x) >= 0.01, sigmas)) == 0:
            #     break
            # 一次训练一个样本，一次更新所有特征函数的权重w值
            self.w = [self.w[i] + sigmas[i] for i in xrange(self.n)]

    def predict(self, testset):
        results = []
        for test in testset:
            # 基于训练得到的特征函数，预测新的待检测样本在最大熵模型下的P(Y|x)的argmax(Y)值
            result = self.cal_probality(test)
            results.append(max(result, key=lambda x: x[0])[1])
        return results


def rebuild_features(features):
    '''
    将原feature的（a0,a1,a2,a3,a4,...）
    变成 (0_a0,1_a1,2_a2,3_a3,4_a4,...)形式
    '''
    new_features = []
    for feature in features:
        new_feature = []
        for i, f in enumerate(feature):
            new_feature.append(str(i) + '_' + str(f))
        new_features.append(new_feature)
    return new_features


if __name__ == "__main__":

    print 'Start read data'

    time_1 = time.time()

    path = './data/train_binary.csv'
    pwd = os.getcwd()
    os.chdir(os.path.dirname(path))
    data = pd.read_csv(os.path.basename(path), encoding='gbk')
    os.chdir(pwd)

    raw_data = pd.read_csv(path, header=0)
    data = raw_data.values

    imgs = data[0::, 1::]
    labels = data[::, 0]

    # 选取 2/3 数据作为训练集， 1/3 数据作为测试集
    train_features, test_features, train_labels, test_labels = train_test_split(
        imgs, labels, test_size=0.33, random_state=23323)

    # 将每个像素点作为一个特征维度，构造特征空间
    train_features = rebuild_features(train_features)
    test_features = rebuild_features(test_features)

    time_2 = time.time()
    print 'read data cost ', time_2 - time_1, ' second', '\n'

    print 'Start training'
    met = MaxEnt()
    met.train(train_features, train_labels)

    time_3 = time.time()
    print 'training cost ', time_3 - time_2, ' second', '\n'

    print 'Start predicting'
    test_predict = met.predict(test_features)
    time_4 = time.time()
    print 'predicting cost ', time_4 - time_3, ' second', '\n'

    score = accuracy_score(test_labels, test_predict)
    print "The accruacy socre is ", score

 

7. 基于scikit-learn实验logistic regression

0x1：MNIST classfification using multinomial logistic + L1

# -*- coding:utf-8 -*-

import time
import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import fetch_mldata
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.utils import check_random_state

# Turn down for faster convergence
t0 = time.time()
train_samples = 5000

mnist = fetch_mldata('MNIST original')
X = mnist.data.astype('float64')
y = mnist.target
random_state = check_random_state(0)
permutation = random_state.permutation(X.shape[0])
X = X[permutation]
y = y[permutation]
X = X.reshape((X.shape[0], -1))

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=train_samples, test_size=10000)

# 特征标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# Turn up tolerance for faster convergence
clf = LogisticRegression(C=50. / train_samples,
                         multi_class='multinomial',
                         penalty='l1', solver='saga', tol=0.1)
clf.fit(X_train, y_train)
sparsity = np.mean(clf.coef_ == 0) * 100
score = clf.score(X_test, y_test)
# print('Best C % .4f' % clf.C_)
print("Sparsity with L1 penalty: %.2f%%" % sparsity)
print("Test score with L1 penalty: %.4f" % score)

coef = clf.coef_.copy()
plt.figure(figsize=(10, 5))
scale = np.abs(coef).max()
for i in range(10):
    l1_plot = plt.subplot(2, 5, i + 1)
    l1_plot.imshow(coef[i].reshape(28, 28), interpolation='nearest',
                   cmap=plt.cm.RdBu, vmin=-scale, vmax=scale)
    l1_plot.set_xticks(())
    l1_plot.set_yticks(())
    l1_plot.set_xlabel('Class %i' % i)
plt.suptitle('Classification vector for...')

run_time = time.time() - t0
print('Example run in %.3f s' % run_time)
plt.show()

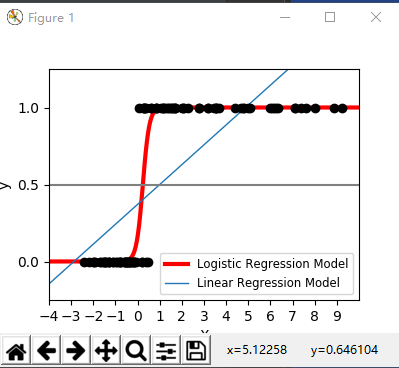
0x2：展示了逻辑斯蒂回归和简单线性回归对非非线性数据集的分类能力

# -*- coding:utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt

from sklearn import linear_model

# this is our test set, it's just a straight line with some
# Gaussian noise
xmin, xmax = -5, 5
n_samples = 100
np.random.seed(0)
X = np.random.normal(size=n_samples)
y = (X > 0).astype(np.float)
X[X > 0] *= 4
X += .3 * np.random.normal(size=n_samples)

X = X[:, np.newaxis]
# run the classifier
clf = linear_model.LogisticRegression(C=1e5)
clf.fit(X, y)

# and plot the result
plt.figure(1, figsize=(4, 3))
plt.clf()
plt.scatter(X.ravel(), y, color='black', zorder=20)
X_test = np.linspace(-5, 10, 300)


def model(x):
    return 1 / (1 + np.exp(-x))
loss = model(X_test * clf.coef_ + clf.intercept_).ravel()
plt.plot(X_test, loss, color='red', linewidth=3)

ols = linear_model.LinearRegression()
ols.fit(X, y)
plt.plot(X_test, ols.coef_ * X_test + ols.intercept_, linewidth=1)
plt.axhline(.5, color='.5')

plt.ylabel('y')
plt.xlabel('X')
plt.xticks(range(-5, 10))
plt.yticks([0, 0.5, 1])
plt.ylim(-.25, 1.25)
plt.xlim(-4, 10)
plt.legend(('Logistic Regression Model', 'Linear Regression Model'),
           loc="lower right", fontsize='small')
plt.show()

Relevant Link:

http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
http://scikit-learn.org/stable/auto_examples/linear_model/plot_sparse_logistic_regression_mnist.html#sphx-glr-auto-examples-linear-model-plot-sparse-logistic-regression-mnist-py
http://scikit-learn.org/stable/auto_examples/linear_model/plot_logistic.html#sphx-glr-auto-examples-linear-model-plot-logistic-py

Copyright (c) 2017 LittleHann All rights reserved