单元测试（107，120）

需求分析

• 1、将运算模块独立出来，单独成类；
• 2、针对提取出来的计算类的接口函数做单元测试。

设计测试框架, 模拟测试数据：

（1）计算类

class MyCalculator
{
public:
    double Add(double m, double n);
    double Subtract(double m, double n);
    double Multiply(double m, double n);
    double Divide(double m, double n);
    int gcd(int m, int n);
    string integer_cal(string op, int m, int n);
    string fraction_cal(string op, int x1, int y1, int x2, int y2);
};

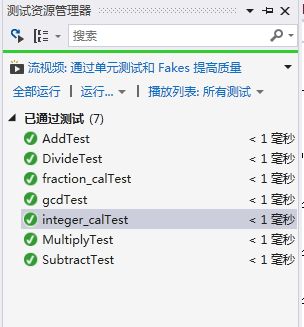
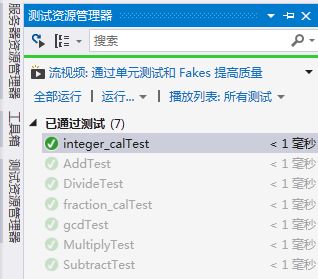
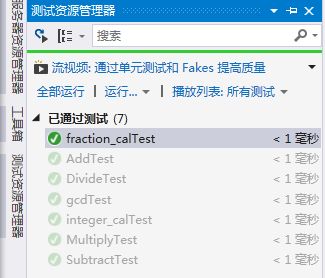
计算类中方法的测试(给出的是测试整数计算和分数计算的测试用例，计算方法支持约分)

    TEST_METHOD(integer_calTest)
        {
            string result = "8";
            Assert::AreEqual(test->integer_cal("+",5,3), result);

            result = "6";
            Assert::AreEqual(test->integer_cal("-", 9, 3), result);

            result = "27";
            Assert::AreEqual(test->integer_cal("*", 9, 3), result);

            result = "3";
            Assert::AreEqual(test->integer_cal("/", 9, 3), result);
            
            result = "NO";
            Assert::AreEqual(test->integer_cal("/", 9, 0), result);

            result = "-1";
            Assert::AreEqual(test->integer_cal("-", 0, 1), result);

            result = "NO";
            Assert::AreEqual(test->integer_cal("++", 9, 1), result);

        }

        TEST_METHOD(fraction_calTest)
        {
            string result = "5/6";
            Assert::AreEqual(test->fraction_cal("+", 1, 2, 1, 3), result);

            result = "1/6";
            Assert::AreEqual(test->fraction_cal("-", 2, 3, 1, 2), result);

            result = "1/6";
            Assert::AreEqual(test->fraction_cal("*", 1, 2, 1, 3), result);

            result = "2/3";
            Assert::AreEqual(test->fraction_cal("/", 1, 2, 3, 4), result);

            result ="NO";
            Assert::AreEqual(test->fraction_cal("-", 2, 0, 1, 2),result);
            
            result = "-1";
            Assert::AreEqual(test->fraction_cal("-", 1, 2, 3, 2), result);

        }

所有测试的结果截图

（2）测试过程中，遇到无法打开.dll、.obj等文件，上网查询后根据网上的步骤操作后即可运行测试；在测试分数计算方法的时候，一开始只有除法的测试运算通过了，找到运算函数后进行相应的修改后，加减乘的测试也能通过了。

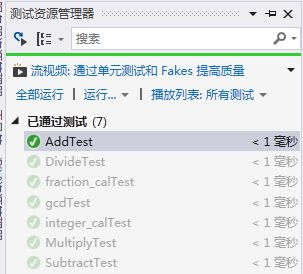
（3）1、测试加法

        TEST_METHOD(AddTest)
        {

            Assert::AreEqual(test->Add(1.0, 2.0), 3.0);
            Assert::AreEqual(test->Add(5.0, 2.0), 7.0);
        }

相应测试截图

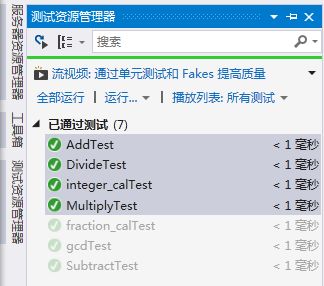
2、测试加减乘除

        TEST_METHOD(AddTest)
        {

            Assert::AreEqual(test->Add(1.0, 2.0), 3.0);
            Assert::AreEqual(test->Add(5.0, 2.0), 7.0);
        }

        TEST_METHOD(SubtractTest)
        {
            Assert::AreEqual(test->Subtract(7.0, 2.0), 5.0);
            Assert::AreEqual(test->Subtract(5.0, 2.0), 3.0);
        }

        TEST_METHOD(MultiplyTest)
        {
            Assert::AreEqual(test->Multiply(7.0, 2.0), 14.0);
            Assert::AreEqual(test->Multiply(5.0, 2.0), 10.0);
        }

        TEST_METHOD(DivideTest)
        {
            Assert::AreEqual(test->Divide(14.0, 2.0), 7.0);
            Assert::AreEqual(test->Divide(6.0, 3.0), 2.0);
        }

相应测试截图

3、测试计算类对于各种参数的支持：

a. 输入是有错误的，例如 “1 ++ 2”，
输入错误时，返回"NO"

            result = "NO";
            Assert::AreEqual(test->integer_cal("++", 9, 1), result);

测试截图

b. 或者是 “ 248 / 0” 怎么办?

            result = "NO";
            Assert::AreEqual(test->integer_cal("/", 9, 0), result);

测试截图

c. 怎么告诉函数的调用者 “你错了”? 把返回的字符串定义为 “-1” 来表示？

            result = "-1";
            Assert::AreEqual(test->fraction_cal("/", 1, 0, 3, 4), result);

            result = "-1";
            Assert::AreEqual(test->fraction_cal("-", 2, 0, 1, 2), result);

d. 那么如果真的计算结果是 “-1” 又怎么处理呢?

将输入错误的返回为"NO"，而计算结果为-1的返回值仍为"-1"

            result ="NO";
            Assert::AreEqual(test->fraction_cal("-", 2, 0, 1, 2),result);
            
            result = "-1";
            Assert::AreEqual(test->fraction_cal("-", 1, 2, 3, 2), result);

测试结果

代码覆盖率

因软件问题，上网查询并按要求配置后仍显示失败。

GIT上交截图

非摆拍照片

小结和感受

通过测试可以提前得知哪些方法出错了，需要在方法定义内进行相应的修改。在测试分数加法时，一开始测试失败了，找到运行的源代码进行相应的处理后，就可以很好的测试了。

在隔了一周之后再看之前的代码，我的体会是：

• 良好的设计：一开始如果就能够设计好，将整个实现过程模块化，在进行测试的时候，能够更快地分离、找到计算模块，并对其进行相应的测试。
• 编码规范：编码的规范首先在看到完整的代码时不会给人一种杂乱无章的感觉，同时变量（函数）的规范性命名能够让从未接触过的人更好的了解变量（函数）的用途、类型。
• 必要的注释：注释能够在后来的接触中让我们更快地了解到方法的用处或者变量的用途。

项目链接

测试代码链接

PSP展示

PSP2.1	Personal Software Process Stages	Time (%) Senior Student(/hour)	Time (%)(/hour)
· Planning	计划	2	1.8
· Estimate	估计这个任务需要多少时间	15	12
· Analysis	需求分析 (包括学习新技术)	5	5
· Coding Standard	代码规范	1	1.5
· Design	具体设计	1.5	1
· Coding	具体编码	5	4
· Test	测试（自我测试，修改代码，提交修改）	1	1.5
Reporting	报告	1	1