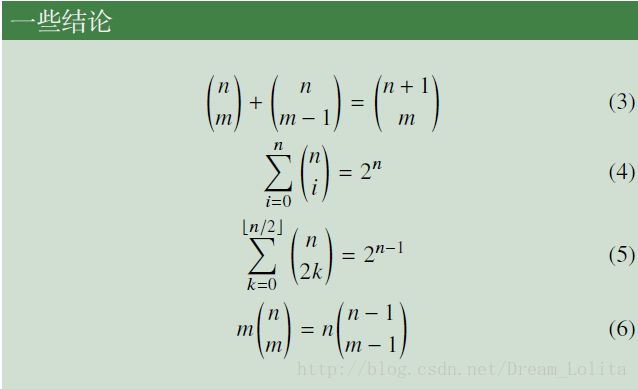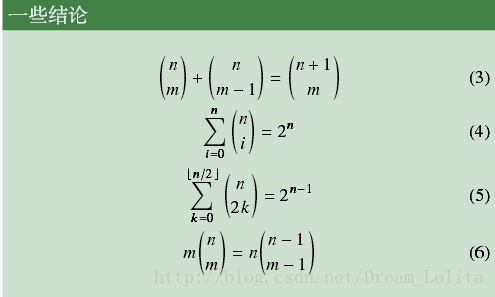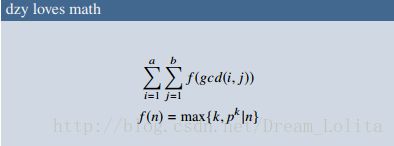【QBXT】学习笔记——Day10数学
今天还是数学。
依旧十分慌张。
然而有些内容昨晚无聊的时候讲了。
======================分割线========================
今天因为来的比较晚，所以前面的内容多用图片辣。
后面有机会再写公式。
引入题：从1到 n n 中选择最多的数，使它们两两互质，问最多能选择多少个。
好无聊的题，去后一半就行了，因为 x x 和 2x 2 x 只能选一个。
接下来是一大段图片：
)
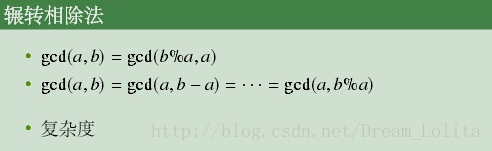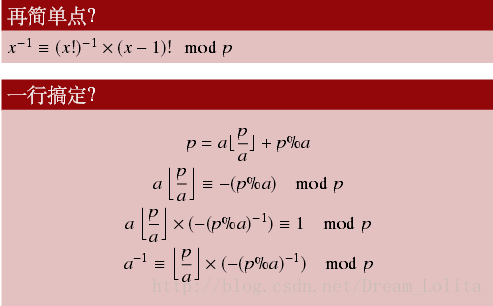
原根一般用于 NTT N T T ，其实原根貌似还挺多的。一般来说如果给出了模数，我们再写一个程序跑一下原根有什么就行，当然在线测试也不会很慢，下面是方法：
我们要验证原根，等同于验证 ap−1 a p − 1 以前，没有任何幂次与它同余。
我们也可以得出：
设 s<p s < p ，若 as=1,ap−1=1，那么s|(p−1) a s = 1 , a p − 1 = 1 ， 那 么 s | ( p − 1 )
这样的话其实显然我们只需要测试 p−1 p − 1 的所有极大因子幂次模p的值即可
若 p−1=pa11∗pa22∗⋯∗pakk p − 1 = p 1 a 1 ∗ p 2 a 2 ∗ ⋯ ∗ p k a k
极大因子 d=(p−1)/pi d = ( p − 1 ) / p i ，显然一共有 k k 个极大因子。
需要所有极大因子模p不为1。
接下来是BSGS，其实类似Meet in the Middle的想法。
就是从两头往中间暴力的。像Meet in the Middle可以应用在状压什么的。
算法大概是求个 ϕ ϕ ,打个表，然后暴力一下。
然后数论一天到晚就是互质变成不互质- -
思想就是每次提出一个公共因子，大概是用
a×bmodc×b=amodc×b a × b mod c × b = a mod c × b 这个式子吧。
具体过程大概是像：
我们令
则有
这样
所以说可以这么做233
Miller−Robin M i l l e r − R o b i n 素性测试
快速验证p是否为素数
利用费马小定理 ap−1modp=1 a p − 1 mod p = 1 ，可以选取若干a，利用快速幂判断模 p p 后是否为1
能骗过底数为 a a 的合数成为以 a a 为底的伪素数
能骗过所有小于 p p 的底数的合数称为 Carmichael C a r m i c h a e l 数(比如561)
所以这类数要加强测试。
然而这是一个假的素性测试，因为很可能被卡掉。
考虑到如下事实：如果 p p 是素数，且 x2modp=1 x 2 mod p = 1 则 x x 等于1或-1
因此我们将 p−1 p − 1 分解为 d2r d 2 r ，先计算 ad a d ，再一直平方，检查每次平方结果是否为1，若是则判断前次结果是否为+1或-1（二次探测）。
合起来就是完整的MR素性测试。
通过以 a a 为第的素性测试的合数，被称为以 a a 为底的强伪素数。(2,2047)
所以还是要多用几个数去算233.
Pollard−Rho P o l l a r d − R h o 分解质因数
先素性测试
随机 m m 个数，两两做差判断是否为 n n 的素数，然后递归分解
当 m n−−√ m n 时，概率约为0.5
随机m个数，两两做差与 n n 求 gcd g c d ，然后递归分解，概率大大提升。
它的准确率之高甚至不需要两两作差qwq。
所以我们利用随机函数 f(x)=x2+amodp f ( x ) = x 2 + a mod p ，每次生成两个随机数，作差求 gcd g c d 即可。（其中a是一个你随意给的数，原论文是2）
当然这个递归过程可能会成环，所以我们需要使用 Floyd F l o y d 判环法。
利用一个两倍速的指针，
算法流程大概是：
1.对 n n 进行素性测试
2.随机选取 a a 和大素数 p p
3.随机起始点 x x 和两倍速点 y y ，我们可以将 x x 和 y y 看作两个不相干的东西。
4. x=f(x),y=f(f(y)) x = f ( x ) , y = f ( f ( y ) )
5.如果 x=y x = y 则已经循环，尝试重新分解，即返回第3步
6.利用 x−y x − y 与 n n 做 gcd g c d ，如果可约则退出，否则返回第4步
算法复杂度是 n−−√4 n 4
然后就要开始讲反演了，十分慌张。
不过先讲了一些关于取模的东西0.0.
几条公式：
用这个东西我们可搞一搞快速乘这玩意：
当模数较大时，我们可以这样子：
上面这个东西就是一直拆一直拆，所以应该是 logn l o g n 的复杂度。
当模数较小时，我们可以这样子：
然后就拆开这个式子分步计算即可。
完全积性函数：
没有任何条件， f(x)×f(y)=f(xy) f ( x ) × f ( y ) = f ( x y )
数论积性函数
当 x x 和 y y 互质下， f(x)×f(y)=f(xy) f ( x ) × f ( y ) = f ( x y ) 。
反演在这：
来之前自己的学习
VFK的反演魔术
然后因为我不想打一大堆一大堆的数学公式了，所以贴图吧
最菜的题目：
还有一些其他的东西：
啊，什么都不想敲了。已经很晚了
接下来是矩阵相关
线性基一些课上没讲的看这里
下面是一些定义
线性无关：一组向量 vk v k ，如果不存在非全零数列 ak a k ，使得 ∑aivi=0 ∑ a i v i = 0 ,则称这组向量线性无关。
线性相关：存在非全零数列 ak a k ，使得 ∑aivi=0 ∑ a i v i = 0
例子：
(1,0),(1,2) ( 1 , 0 ) , ( 1 , 2 ) 线性无关
(1,0,1)(2,3,3)(0,3,1) ( 1 , 0 , 1 ) ( 2 , 3 , 3 ) ( 0 , 3 , 1 ) 线性相关
基底：一组可以生成整个线性空间的线性无关组（任何向量均可由基底表示出来）
其实这个东西从数学几何上来理解会比较简单。
以 R3 R 3 为例子， (1,0,0)(0,1,0)(0,0,1) ( 1 , 0 , 0 ) ( 0 , 1 , 0 ) ( 0 , 0 , 1 ) 是常见的一组基。
同样 (e,0,π)(2,3,3)(0,0,976528) ( e , 0 , π ) ( 2 , 3 , 3 ) ( 0 , 0 , 976528 ) ,也可以作为一组基。
特殊线性空间
Fp在Fnp F p 在 F p n 上的乘法作用生成的线性空间。
特别地， p=2 p = 2 时，乘法表现为 and a n d 运算，加法表现为 xor x o r 运算
例如： 0b101,0b011,0b001 0 b 101 , 0 b 011 , 0 b 001 是一组 F32 F 2 3 的一组基
这个东西可以这样理解：算了不用理解了。
大概就是平面图上有两个环，将这两个环亦或一下还是一个环（即使断开了）
模板题
给出一组 Q Q 上线性方程组，求出它的一组解或判断无解。
高斯消元即可。
模板题+
给出一组 Q Q 上模线性方程组，求出它的一组解或判断无解。
模线性方程组，解的数量一定是有限的，我们可以将除法操作转化为逆元乘法。
模板题++
给出一组 Q Q 上一组线性关系，求出它的线性基。
整个过程和高斯消元的理论是一样的，就是一直消元，看哪个向量是没有用的。
话说 n×n n × n 的方阵，消元时向量貌似是线性无关的。
然后消元后如果消出了一行0，说明这个矩阵没有逆矩阵。
简单题
单位矩阵：
对角线为1，其他全为0.
逆矩阵：
若 AB=BA=I A B = B A = I ，则 B B 是 A A 的逆矩阵， B B 可以记为 A−1 A − 1
给出一个矩阵 An×n A n × n ，求出它的逆矩阵或者不可逆。
行列式
行列式仅对方阵有定义：
一些结论：
某一行加上另一行的若干倍，行列式不变（就像一个立方体中间割一条线，然后上下的总高度不变，上下底面积不变，中间层位置平移。）
某两行交换：行列式变号
某一行乘 k k ：行列式乘 k k
矩阵转置：行列式不变（转置指 (i,j)变成(j,i) ( i , j ) 变 成 ( j , i ) ）
某一列(行)分裂：行列式分裂求和
这些东西我们都可以用从物理意义来解释一下。
然后我们怎么求行列式的值呢？
利用上面的结论，类似高斯消元，将这个行列式变成上三角行列式
显然只有对角线才能累加进值里。（因为其他斜线都会进入下三角，从而变成0）
行列式pro
给出一个 n n 阶整系数矩阵的第一行，问是否有可能填充剩余位置，使得行列是为K，并给出一个可行方案 n<=200,k<=1018 n <= 200 , k <= 10 18
根据上面的几个结论，我们也可以很容易地构造出来这个东西。
因为某一列加上另一列的若干倍，行列式不变，那么我们可以通过辗转相除，令第一行得出一个1，这样我们显然可以构造出一个矩阵，使它的结果为k，然后我们再将构造出的矩阵倒推回去即可。
生成树定理
邻接矩阵( A A )：每个格子值为0或1， (i,j) ( i , j ) 若为1表示 i i 和 j j 之间有一条边，否则没有。
度数矩阵( D D )：左上到右下有值的矩阵， (i,i) ( i , i ) 的值为点 i i 的度数。
基尔霍夫矩阵( S S )： D−A D − A ,即上面两个对应位置相减.
主子式：一个矩阵去掉一行一列得到的矩阵。
然后一幅图的生成树个数就是 S S 任意一个主子式的行列式。
对于无向图来说，删掉一行一列有“选根”的思想。
对于无向图来说， D D 的定义改成出度矩阵。
那么有向图以 i i 为根的内向树的个数主子式 Si S i （删掉第 i i 行 i i 列）的行列式。
简单题：
N×M N × M 的格状矩形，每个格子是房间或是柱子。相邻的格子之间都有墙隔着你想要打通一些墙，使得所有房间能够互相到达。在此过程中，你不能把房子给打穿，或者打通柱子(以及柱子旁边的墙)同时,你希望任意两个房间之间都只有一条通路
统计一共有多少种可行的方案，对 109+7 10 9 + 7 取模。 N,M<=10 N , M <= 10
简单题+：将模数换成 Q,Q<=1018 Q , Q <= 10 18
这个东西就是前提到的生成树个数计算辣，只是这个模数有点奇怪。
对于简单题+，我们用 CRT C R T 将 Q Q 转换为 Piki P i k i ， Pi P i 是素数，那么现在模一个素数的指数幂。对于行列式求值，若第一列所有数模 Pi P i 都为0，显然我们可以提取一个公因数 Pi P i 出去答案就是 Pi×新行列式值 P i × 新 行 列 式 值 ，否则我们任意找到一个模 Pi P i 不为0的，求一个逆元消元。
特殊的矩阵
稀疏矩阵：循环ijk的顺序影响计算效率（有些是0的，不用算）
循环矩阵（类似于第一行1234，第二行2341，第三行3412.第四行4123）：自乘作快速幂时只用算出第一行的值，然后平移一下就行了，降低一维的复杂度。
对称矩阵：也相当于算一半矩阵卡常数用。
分块矩阵：分块计算玄学优化。
还是简单题？？
给出一个有向图，起始点为 1 1 ，求 k k 步走到 n n 号点的方案数。
显然是邻接矩阵的k次方。
如果是要求 1 k 1 k 步的答案，我们可以新建一个点 n+1 n + 1 ，然后终止节点(这里是 n n )向 n+1 n + 1 号点连一条边， n+1 n + 1 号点自己再向自己连一条边。
这样子相当于每次答案都累加了起来。
以上两个最后都要乘一个起始点向量。
简单题++
给出一个有向图，起始点为1，边权为转移概率，求第 k k 步在 n n 号点的概率。
一个自动机，是昨天的问题，然而其实差不多。
递推求解
An=uAn−1+vAn−2 A n = u A n − 1 + v A n − 2 求 An A n , n<=1018 n <= 10 18
An=uAn−1×An−2 A n = u A n − 1 × A n − 2 求 An A n , n<=1018 n <= 10 18
凯莱哈密尔顿定理(CH定理)
这里实在是写不动了啊，直接拿乱的课上笔记应该看得懂。
卷积
首先要了解一堆关于复数的知识：
对于第一个公式可以证明的啊：
上最强公式
e2πi e 2 π i 是等于1的，所以就这样了。
还有这个
心态炸了啊，一堆东西，然后我十分地困。
所以我就贴图片吧。
NTT
一些题目：
K K 进制大整数乘法
给出两个 K K 进制数，求答案的 L L 进制数是多少。
直接卷积式转移然后得到答案后再转换。
卷积式dp转移：
Hn=∑Fi×Gn−i−1 H n = ∑ F i × G n − i − 1
构造生成函数 f(x)=∑Fixi f ( x ) = ∑ F i x i 和 g(x)=∑Gixi g ( x ) = ∑ G i x i
类阶乘函数：
求 f(x)=Πmi=1(x+i) f ( x ) = Π i = 1 m ( x + i ) 的系数表示
用分治+FFT来做，时间复杂度是 O(nlog2n) O ( n l o g 2 n ) 。（听说是简单题）
分治+FFT的思想还是很好用的
集合取数
给定整数集合S，试问有多少种从S中取出n个数（可重复）的方案，使选出的数的积对素数p取模为x，方案数对1004535809取模。 p<=8000,n<=109 p <= 8000 , n <= 10 9
一看这题，基本上就是NTT了，其中这个选出数的积这个东西比较烦，因此我们用原根将乘法转化为加法。
我不会做。
接下来是计数原理.写到这我已经绝望了
一些结论:
一道题目：
n个人坐在m张凳子上，m张凳子形成圆环，任意两个人在环上的距离不小于k，求方案数（循环反转视为不同）。 0<n,m<106,0<k<100 0 < n , m < 10 6 , 0 < k < 100 ，多组数据。
例子 2 5 1，ans=5
先考虑前 n−1 n − 1 个人，并删去他后面的 k k 张凳子。
方案数就是 (m−(n−1)kn) ( m − ( n − 1 ) k n )
对于环的情况，考虑破环成链。取长为 k+1 k + 1 的连续椅子，其中最多能放一个人。
若放了一个人，则问题转化为 m−2k−1 m − 2 k − 1 的链上放 n−1 n − 1 个人。
若未放人，则问题转化为 m−k−1 m − k − 1 的链上放 n n 个人。
然后是 Fibonacci F i b o n a c c i 数列的一些东西：
特征方程之类的东西这里就不怎么说了。
接着讲很有意义的生成函数！
一堆东西一堆东西一堆东西。
求长度为n的括号序列个数
折线定理三题。
第一第二问都比较简单。
第三问的模型转化还不是很懂，回去慢慢弄懂。大概是将这个方格进行折叠若干次什么的。
BZOJ3028食物（权限题）
一道显然是生成函数的题目。
经过一阵推理答案是 (n+2)(n+1)n6 ( n + 2 ) ( n + 1 ) n 6
下面是一堆我已经没什么心力看的东西。
其中 |G| | G | 是指转置。
这个东西极其暴力，下面用一张图解释循环同构（例1）：
接下来是 Polya P o l y a 计数原理，依旧是组合数学的东西啊。
看来组合数学还是要好好看。
Polya P o l y a 其实就是将前面的大暴力的枚举的东西改变了。
它是对染的颜色进行置换什么的0.0 颓废.jpg
简单题：
这些题都是很显然的题目，在这里就不说了，好累啊。
到时去做一下就好了。
康托展开：
求排列 an,an−1,…,a1 a n , a n − 1 , … , a 1 的排名T
T=∑rank(ai)×(i−1)! T = ∑ r a n k ( a i ) × ( i − 1 ) !
rank(ai) r a n k ( a i ) 表示 a1～ai a 1 ～ a i 中第 ai a i 的排名(从0开始)
例如 (4,2,1,3)=3∗3!+1∗2!+0+0=20 ( 4 , 2 , 1 , 3 ) = 3 ∗ 3 ! + 1 ∗ 2 ! + 0 + 0 = 20
至于这个东西有什么用，貌似没什么用大约可能会有那种求第 k 字典序大的题，
然后可以和数据结构结合起来，用来二分 or 快速统计
飞快到了博弈论
其实后面很多东西blog上都是有的啊，在这里放几个blog算了。
从零开始
博弈基础
博弈详解
SG函数
其实只要记住一个重要推论- -
一切都是破石头门的选择！
POJ3537 Crosses and Crosses
1 × n 的棋盘上，两人轮流行动，每次选择一个空格子画 X。
若某人操作后，出现了连续 3 个 X，则他获得胜利。
问先手是否必胜.。
这题是博弈论入门题。
某清华姚班大神如是说：大胆猜测，从不验证，每次AK
因此我们考虑怎么求这个SG函数
这题相当于放了x的位置，左右4格都不能再放x了，谁无处可放就输。
直接枚举后继状态，暴力求SG函数即可。
例： 0000000->x..0000 / .x..000 / ..x..00 / 0..x..0 / 00..x..
啊，各种散题也不想动。
这道暴力水题。
这道最简单的反演题。
这是一道真正的反演题啊，反演三次就好了。UOJ62
VFK:三个莫比乌斯反演掷地有声。
看来数学部分要学很久很久啊。