常系数齐次线性递推算法学习

简介

定义：设有数列$\{a_n\}满足递推关系a_n=\sum _{i=1}^k{a}_{n-i}{f}_i$，则称该数列满足$k$阶齐次线性递推关系。

求法

现在我们从最基础的矩阵快速幂开始一步一步优化求$a_n$的时间复杂度。

矩阵快速幂

直接上矩阵快速幂来优化递推即可，时间复杂度为$O(k^{3}lo{g}_n)$，非常不优秀，因此我们考虑用更快的方法求出$a_n$。

在我们知道了$a_1,a_2,...a_k$之后想推出$a_n$的方法可以借鉴矩阵快速幂的方法，构造一个$k\ast k$的矩阵$M$来完成递推，关键就是优化求$M^n$的时间复杂度了，这里我们引入一个叫做特征多项式的东西。

特征多项式

一些定义

特征值，特征向量：$对于一个矩阵A,若\exists 常数\lambda 和向量v满足\lambda v=Av$则称向量$v$为矩阵$A$的一组特征向量，$\lambda$为矩阵$A$的一组特征值。
特征多项式，特征方程，特征值：我们对上面的关系式进行变换：$(\lambda E-A)v=0$，学过线性代数的都知道这个方程有解的充要条件是$det(\lambda E-A)=0$，于是我们将$det(\lambda E-A)$看成一个$k$次多项式$f(x)$，我们将$f(x)=0$这个方程称作特征方程，将$f(x)$称作特征多项式，而特征方程的$k$个根就是$k$个特征值。
由于一共有$k$个解，因此我们可以换一种形式来表示$f(x)$：$f(x)={\prod }_{i=1}^k(x-{\lambda }_i),{\lambda }_i指第i个特征值即第i个解$

Cayley-Hamilton定理

这是特征根多项式的一个重要性质，叙述如下：
设$A$是数域$P$上的$N$阶矩阵，其特征多项式$f(\lambda )=|\lambda E-A|={\lambda }^N+b_1{\lambda }^{N-1}+b_2{\lambda }^{N-2}+...+b_{N-1}\lambda +b_N$。
则$f(A)=A^N+b_1{A}^{N-1}+b_2{A}^{N-2}+...+b_{N-1}A+b_N=O$，即$f(\lambda )$为化零多项式。

递推优化

考虑$M$的特征多项式$f(x)$，这是一个$k$次多项式。
不妨对$M^n$和$f(M)$做一个多项式除法，令$M^n=f(M)g(M)+r(M)$，考虑到$f(x)$是$M$的特征多项式，因此$f(M)=O\Rightarrow r(M)=M^n$，于是问题转化成了求$M^n\%f(M)$，并且我们已知这个多项式次数最多是$k-1$
然后就只用求出$f(M)$即可。
推导过程摘自$DZYO$的博客：


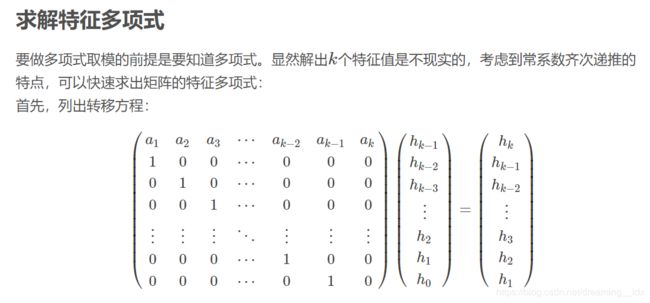
求出来之后对多项式取模即可。
直接$O(k^2)$取模总时间复杂度是$O(k^{2}lo{g}_n)$的。
当然可以更加毒瘤，我们用FFT来优化把总时间复杂度降到$O(klo{g}_{k}lo{g}_n)$