pytorch系列 --3 Variable，Tensor 和 Gradient

Variable & Automatic Gradient Calculation

• Tensor vs Variable
• graph and gradient
  注意，在pytorch0.4中，tensor和pytorch合并了。
  https://pytorch.org/blog/pytorch-0_4_0-migration-guide/
  torch.Tensor 和 torch.autograd.Variable 是同一个类，更准确的说，torch.Tensor 也能像旧的Variable一样
  追踪历史，进行梯度计算等。Variable 仍然正常工作，但是返回的对象是torch.Tensor,这意味着不需要在代码中使用Variable（Tensor）了。

但是此篇文章主要讲述Variable的相关知识，将在下一篇在文章中讲述pytorch0.4的具体变化

引进库

import torch
from torch.autograd import Variable

Tensor 和 Variable

Variable:

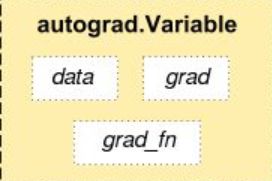
autograde.Variable是一个类，在使用tensor_variable = autograde.Variable(tensor)后，
tensor_variable 有三个重要的属性：

• data:保存着tensor_variable 的tensor向量
• grad: 保存tensor_variable 的梯度值
• grad_fn: 保存创建tensor_variable 的函数
  此外，还有一个属性requires_grad确定tensor_variable 是否具有求导的功能。
  以上Variable就是pytorch实现反向传播最核心的先决条件。
  接下里来看一下Variable的具体功能：

1） 声明 declaration

x_tensor = torch.Tensor(3,4)
x_tensor

out:

-12170.8672 0.0000 -12170.8672 0.0000
0.0000 0.0000 0.0000 0.0000
-12170.9453 0.0000 -12170.9453 0.0000
[torch.FloatTensor of size 3x4]

使用Variale转换Tensor

x_variable = Variable(x_tensor)
x_variable

out:

12170.8672 0.0000 -12170.8672 0.0000
0.0000 0.0000 0.0000 0.0000
-12170.9453 0.0000 -12170.9453 0.0000
[torch.FloatTensor of size 3x4]

2)Variable的属性

.data :Variable的Tensor数据

# .data -> wrapped tensor 
x_variable.data

out:

-12170.8672 0.0000 -12170.8672 0.0000
0.0000 0.0000 0.0000 0.0000
-12170.9453 0.0000 -12170.9453 0.0000
[torch.FloatTensor of size 3x4]

.grad: variable的梯度值

# .grad -> gradient of the variable
print(x_variable.grad)

out:

None

.reqires_grad: variable是否能进行梯度计算

# .requires_grad -> whether variable requres gradient
print(x_variable.requires_grad)

x_variable = Variable(x_tensor,requires_grad=True)
x_variable.requires_grad

.grad_fn: variable的创建函数

y = x_variable * 2

print(y.grad_fn)

out:

3. Graph & Variables

先看一个简单的计算图的例子：
可以简单的计算出w的梯度是x，也就是2，其余x，b的同样的可以简单计算出。

w = Variable(torch.Tensor([1]), requires_grad=True)
x = Variable(torch.Tensor([2]), requires_grad=True)
b = Variable(torch.Tensor([3]), requires_grad=True)
y=w*x+b  # y=1*x +2

y.backward()
print(w.grad, x.grad, b.grad)

out:

2 1 1

接下来，将x的requires_grad=True改为requires_grad=False,此时求x的grad：

可以发现x的grad是None，也就是没有计算保留x的梯度

w = Variable(torch.Tensor([1]), requires_grad=True)
x = Variable(torch.Tensor([2]),  requires_grad=False)
b = Variable(torch.Tensor([3]), requires_grad=True)
y=w*x+b  # y=1*x +2

y.backward()
print(x.grad)

out:

2 None 1

如果求梯度的值是一个向量张量，而非标量张量呢？假设对于z是一个长度为4的一维张量。那要求z,4个维度上的梯度值了，这个概念在数学中并不陌生，比如y是多维输出，那么要在y每一个维度上求梯度值。此时要使用gradients参数，要求gradients的size和y的size相同.同时:
$$gradients每一维度上的值\ast y每一维度上的梯度值为最终参数中grad保留的值$$

下面通过例子看一下：
看一下输出：
第2行只计算了z第一个值得梯度，第3行只计算了z第2个值得梯度，
而第4行计算了z所有是个值得输出，第5行将第四行的输出在乘以gradients的每一个值得到最终的梯度。

x = Variable(torch.FloatTensor([1, 2, 3, 4]), requires_grad=True)
z = 2*x
print(z, z.size())
# do backward for first element of z
z.backward(torch.FloatTensor([1, 0, 0, 0]))
print(x.grad.data)
x.grad.data.zero_() #remove gradient in x.grad, or it will be accumulated

# do backward for second element of z
z.backward(torch.FloatTensor([0, 1, 0, 0]))
print(x.grad.data)
x.grad.data.zero_()

# do backward for all elements of z, with weight equal to the derivative of
# loss w.r.t z_1, z_2, z_3 and z_4
z.backward(torch.FloatTensor([1, 1, 1, 1]))
print(x.grad.data)
x.grad.data.zero_()

z.backward(torch.FloatTensor([1, 0.1, 0.01, 0.001]))
print(x.grad.data)

out:

tensor([2., 4., 6., 8.], grad_fn=) torch.Size([4])
tensor([2., 0., 0., 0.])
tensor([0., 2., 0., 0.])
tensor([2., 2., 2., 2.])
tensor([2.0000, 0.2000, 0.0200, 0.0020])

对于神经网络而言，最后的loss都是一个标量形式，所以不需要传入gradients，采用标量形式的梯度计算即可。

from torch.autograd import Variable
import torch
x = Variable(torch.FloatTensor([[1, 2, 3, 4]]), requires_grad=True)
z = 2*x
loss = z.sum(dim=1)

# do backward for first element of z
z.backward(torch.FloatTensor([[1, 0, 0, 0]]))
print(x.grad.data)
x.grad.data.zero_() #remove gradient in x.grad, or it will be accumulated

# do backward for second element of z
z.backward(torch.FloatTensor([[0, 1, 0, 0]]))
print(x.grad.data)
x.grad.data.zero_()

# do backward for all elements of z, with weight equal to the derivative of
# loss w.r.t z_1, z_2, z_3 and z_4
z.backward(torch.FloatTensor([[1, 1, 1, 1]]))
print(x.grad.data)
x.grad.data.zero_()

# or we can directly backprop using loss
loss.backward() # equivalent to loss.backward(torch.FloatTensor([1.0]))
print(x.grad.data)

代码最后一行的输出为：
out：

2 2 2 2
[torch.FloatTensor of size 1x4]

可以看出使用loss可以达到与调用z.backward(gradients)相同的作用。该问题参考stackoverflowhttps://stackoverflow.com/questions/43451125/pytorch-what-are-the-gradient-arguments